4.2. Критерии оптимальности

Критерий оптимальности служит числовым показателем качества САУ и задается в виде функционала

J=J(u(t),y(t)).

Функционал является естественным обобщением понятия « функция ». В ТАУ широко применяют интегральные функционалы, характеризующие качество САУ. В общем случае интегральный функционал зависит от выходных координат , управляющих и возмущающих воздействий

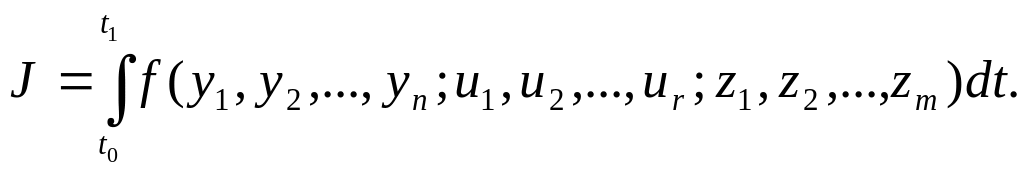
Достижения максимального (или минимального) значения этого функционала указывает на оптимальное поведение или состояние САУ.

В качестве критерия оптимальности J могут быть применены интегральные оценки качества процесса регулирования. Например, при использовании квадратичной оценки САУ будет оптимальной, если . Этот критерий оптимальности характеризует суммарную ошибку регулирования и минимальные отклонения выходной величины. Для обеспечения минимума ошибки регулирования стохастических САУ используют СКО . В этом случае критерий оптимальности

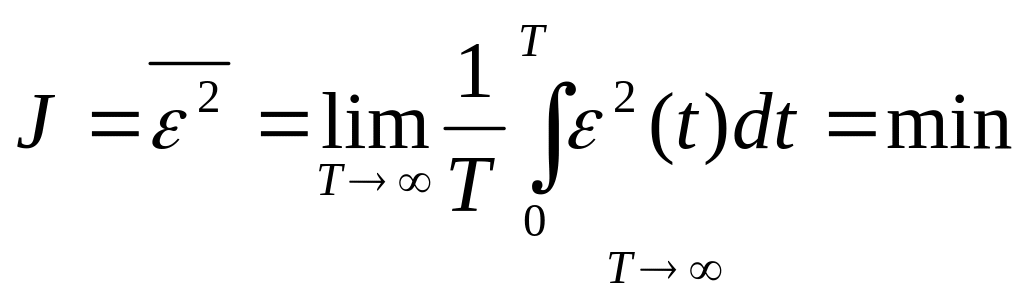
позволяет определять параметры САУ и оптимальную передаточную функцию при условии минимума СКО системы.

В тех случаях, когда необходимо обеспечить наилучшую работу САУ в наихудших возможных условиях, используют критерий оптимальности, называемый минимаксным.

Таким образом, задачу оптимального управления формулируют следующим образом: при заданных уравнении ОУ, ограничениях и краевых условиях требуется найти такие программные управление или управление с ОС и фазовую траекторию , при которых критерий принимает минимальное (или максимальное) значение. Управления и и траекторию называют оптимальными.

4.3 Методы теории оптимального управления

4.3.1 Общие сведения

Задача оптимизации динамики САУ сводится к математическому определению экстремума функционала. Для этого следует дать приращение аргументу функционала и выяснить, как изменится его значение. Приращение или вариация аргумента изменяющегося произвольно функционала J[x(t)] есть разность между двумя близкими функциями

Понятие вариации отличается от понятия дифференциала dx. Оба понятия связаны с бесконечно малыми изменениями функции x(t). Различие состоит в том, что dx порождается бесконечно малым изменением dt независимой переменной t, а своим возникновением обязан новой функции При этом варьируется лишь функция при постоянстве , т.е. =0. Варьирование функции есть переход её от первоначальной функции к близкой, мало отличающейся от неё функции , и сравнение их значений при определенных значениях независимой переменной t.

Нахождение экстремумов функционалов производится методами вариационного исчисления.

4.3.2 Классический метод вариационного исчисления

Для изучения переходных процессов в САУ используют следующий функционал

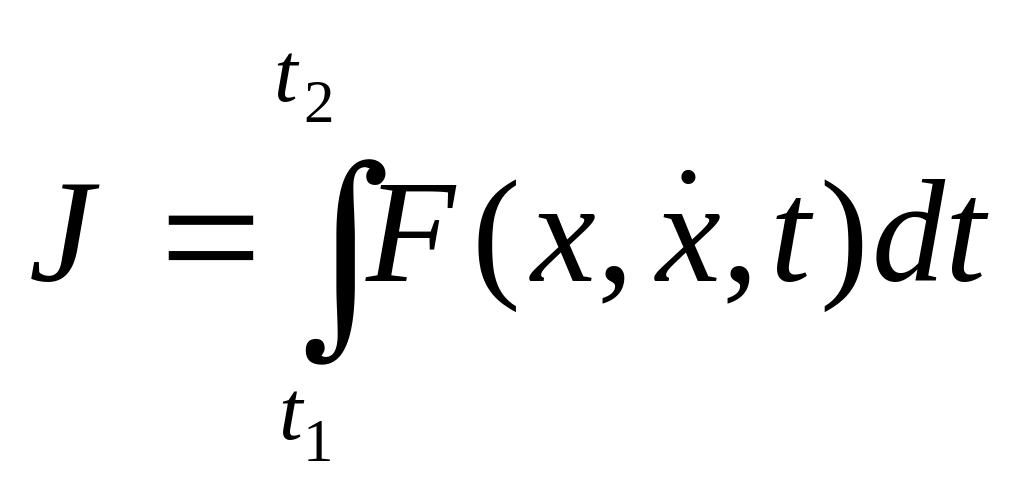, (4.1)

где x=x(t)- траектория обобщенного движения; - скорость движения; и - начальный и конечный моменты времени. Условие существования экстремума функционала J определяют следующим образом. Варьируют подынтегральную функцию x(t) и её производную (t) и определяют приращение интеграла (4.1) разложением его в ряд Тейлора. Отбрасывая малые члены ряда, получают первую вариацию функционала

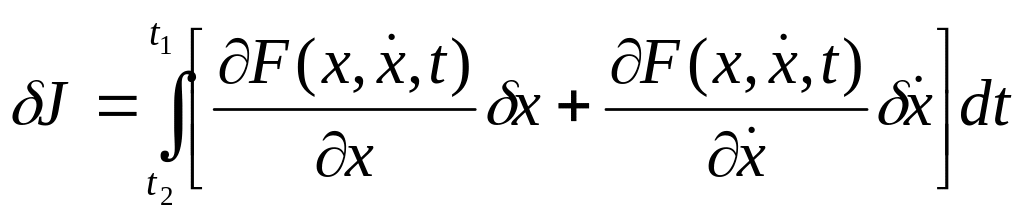. (4.2)

Необходимым условием существования экстремального значения интеграла J (4.1) является равенство нулю его первой вариации . Для нахождения экстремума функционала J при заданных граничных условиях =0 и =0 приравнивают к нулю выражение (4.2)

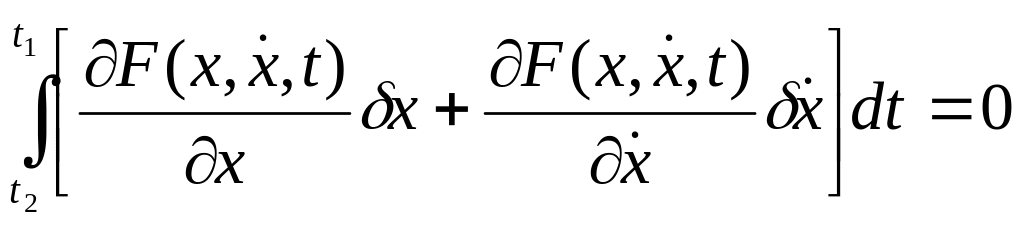. (4.3)

Это равенство должно выполняться для любой вариации, которая удовлетворяет граничным условиям и . Интегрируя по частям (4.3), находят ,что равенство нулю возможно лишь при условии

. (4.4)

Уравнение (4.4) называют дифференциальным уравнением Эйлера. Постоянные интегрирования этого уравнения определяют из граничных условий. Решение уравнения Эйлера является необходимым и достаточным условием экстремума интеграла (4.1) при заданных граничных условиях. Для определения соответствия экстремума функционала минимуму или максимуму можно ограничится проверкой знака второй производной (условие Лежандра): при - минимум; при - максимум функционала.

Использование классического метода вариационного исчисления предполагает, что искомые функции оптимальных процессов являются непрерывными и на координаты выхода и управлений не накладываются ограничения. Поскольку на практике различные ограничения накладываются не только на ОУ, но и на САУ, то возможности использования рассмотренного метода ограничены.