
- •1 Линейные дискретные модели систем управления
- •1.3.2.6 Передаточные функции разомкнутых и замкнутых импульсных
- •2 Нелинейные модели систем управления
- •2.1 Анализ равновесных режимов
- •2.1.1 Основные понятия
- •2.1.2 Структура обобщённой нелинейной сау
- •3 Линейные стохастические модели сау
- •4 Оптимальные сау
- •1 Линейные дискретные модели систем управления
- •Основные понятия о дискретных сау
- •1.2 Классификация дискретных сау
- •1.3 Импульсные сау
- •1.3.1 Понятие об импульсных сау
- •1.3.2 Основной математический аппарат теории дискретных сау
- •1.3.2.1 Структурная схема сау с аим
- •1.3.2.2 Понятие о решетчатой функции
- •1.3.2.3 Понятие о разностных уравнениях
- •1.3.2.4 Дискретное преобразование Лапласа (d-преобразование)
- •1.3.2.6 Передаточные функции разомкнутых и замкнутых импульсных сау
- •Построение переходной характеристики импульсной сау
- •Понятие о частотных характеристиках импульсных сау
- •1.3.2.9 Теорема Котельникова-Шеннона
- •1.3.3 Анализ устойчивости импульсных сау с аим
- •1.3.3.1 Общие сведения
- •1.3.3.2 Алгебраический критерий устойчивости (аналог критерия Гурвица)
- •1.3.3.3 Алгебраический критерий Шур-Кона
- •1.3.4 Аналог критерия Михайлова
- •1.3.5 Аналог критерия Найквиста
- •1.5 Линеаризованные цифровые сау
- •1.5.1 Общие сведения
- •1.5.2 Обобщенная структурная схема цифровой сау
- •1.5.3 Передаточные функции элементов цифровой сау
- •1.5.3.1 Передаточная функция ацп
- •1.5.3.2 Передаточная функция цвм
- •1.5.3.3 Передаточная функция цап
- •1.5.3.4 Структурная схема линеаризованной цас
- •1.5.4 Оценка устойчивости и качества линеаризованной цас
- •1.5.5 Синтез цас
- •2 Нелинейные модели систем управления
- •2.1 Анализ равновесных режимов
- •2.1.1 Основные понятия
- •2.1.2 Структура обобщённой нелинейной сау
- •2.1.3 Типовые нелинейные характеристики
- •2.2 Методы линеаризации нелинейных моделей
- •2.3 Анализ поведения системы управления на фазовой плоскости ( метод фазовых траекторий )
- •2.3.1 Основные понятия
- •2.3.2 Методы построения фазовых портретов
- •2.3.3 Исследование нелинейных сау на фазовой плоскости
- •2.4 Устойчивость положений равновесия
- •2.4.1 Понятие устойчивости нелинейных систем
- •2.5 Первый и второй методы Ляпунова
- •2.5.1 Первый метод Ляпунова
- •2.5.2 Второй метод Ляпунова
- •2.5.3 Определение функций Ляпунова методом Лурье-Постникова
- •2.6 Частотный метод исследования абсолютной устойчивости
- •2.7 Исследование периодических режимов методом гармонического баланса
- •2.7.1 Сущность метода
- •2.7.2 Определение параметров предельных циклов
- •2.7.3 Устойчивость предельных циклов
- •3 Линейные стохастические модели сау
- •3.1 Модели и характеристики случайных сигналов
- •3.2 Прохождение случайных сигналов через линейные звенья и системы.
- •3.3 Анализ и синтез линейных стохастических систем при стационарных случайных воздействиях.
- •4 Оптимальные сау
- •4.1 Задачи оптимального управления
- •4.2. Критерии оптимальности
- •4.3 Методы теории оптимального управления
- •4.3.1 Общие сведения
- •4.3.2 Классический метод вариационного исчисления
- •4.3.3 Принцип максимума
- •4.3.4 Метод динамического программирования.
- •4.4 Синтез оптимальных сау
- •4.4.1 Классификация оптимальных сау
- •4.6 Робастные сау и адаптивное управление
- •4.6.1 Робастные системы управления
- •4.6.2 Самонастраивающиеся (адаптивные) сау
- •4.6.2.1 Понятие об адаптивных сау
- •4.6.2.2 Виды адаптивных систем управления
- •4.6.2.3 Самонастраивающиеся сау со стабилизацией качества управления
- •4.6.2.4 Самонастраивающиеся сау с оптимизацией качества управления
2.3.2 Методы построения фазовых портретов
Фазовый портрет даёт полное
представление о динамике САУ второго
порядка при детерминированных
воздействиях, включая точность,
устойчивость и качество процессов.
Фазовая плоскость является основным
методом исследования нелинейных САУ
второго порядка. Это связано с тем, что
построение фазового портрета выполняют
по дифференциальному уравнению САУ, не
решая его самого. В общем виде ММ САУ
второго порядка имеет вид
![]() Используя подстановку
Используя подстановку
![]() ,
уравнение второго порядка преобразуют
к форме Коши
,
уравнение второго порядка преобразуют
к форме Коши
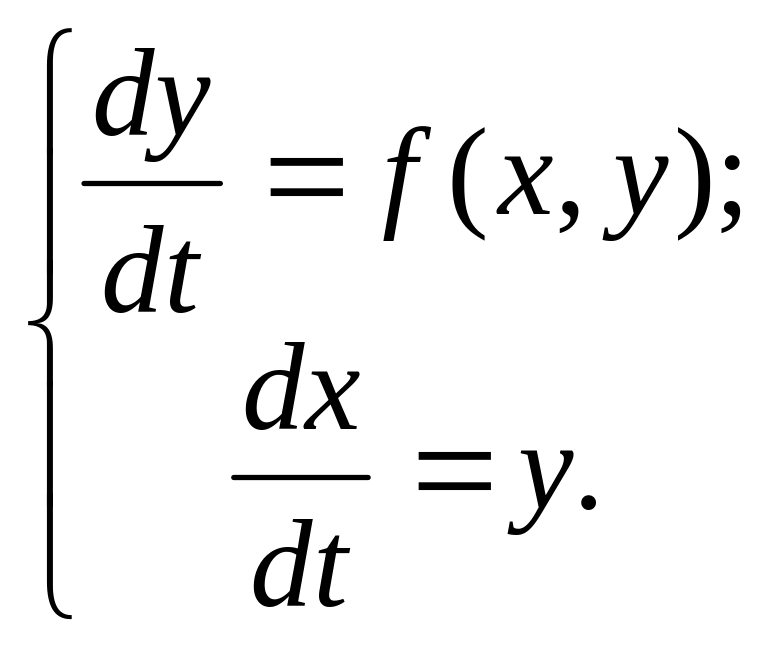
Разделив первое уравнение на второе, получают уравнение фазовых траекторий в виде нелинейного дифференциального уравнения первого порядка
![]() (2.1)
(2.1)
Т.о., путем исключения времени упрощают
задачу, понижая порядок уравнения.
Однако построение траекторий в общем
случае не требует решения и этого
уравнения и может быть выполнено методом
изоклин ( рис.5.13 ). Для этого в начале
на фазовой плоскости строят линии по
алгебраическому уравнению R(x,y)=C,
где С – постоянная, для которой
задаётся ряд произвольных значений
от-![]() до +
.
Каждому значению С соответствует
своя линия. Эти линии называют изоклинами.
Как следует из уравнения ( 5.1 ), для
каждой изоклины
до +
.
Каждому значению С соответствует
своя линия. Эти линии называют изоклинами.
Как следует из уравнения ( 5.1 ), для
каждой изоклины
![]() ,
т.е. изоклина – это геометрическое место
точек с одинаковым наклоном фазовых
траекторий проходящих через эти точки.
По изоклинам строят сами фазовые
траектории.
,
т.е. изоклина – это геометрическое место
точек с одинаковым наклоном фазовых
траекторий проходящих через эти точки.
По изоклинам строят сами фазовые
траектории.
2.3.3 Исследование нелинейных сау на фазовой плоскости
2.4 Устойчивость положений равновесия
2.4.1 Понятие устойчивости нелинейных систем
При исследовании линейных САУ всегда можно переходный процесс
представить в виде суммы переходной
(или свободной) и вынужденной составляющих.
Показателем устойчивости линейной САУ
является стремление к нулю (затухание)
переходной составляющей при
![]() .
.
Решение вопроса об устойчивости нелинейной САУ оказывается значительно сложнее, т.к. в связи с неприменимостью принципа наложения (суперпозиции) невозможно выделить в процессе переходную и вынужденную составляющие. Возможность автоколебаний в нелинейных САУ ещё больше усложняет вопрос.
Для нелинейных САУ введены понятия устойчивости в зависимости от областей возможных отклонений от состояния равновесия и наличия внешних воздействий.
В зависимости от наличия внешних воздействий на САУ все системы управления могут быть разделены на автономные и неавтономные. К последним приложены зависящие от времени воздействия. В отсутствие внешних воздействий САУ считают автономной. Понятие устойчивости автономной системы управления включает: устойчивость равновесия и устойчивость автоколебаний. Понятие устойчивости неавтономной САУ включает в себе устойчивость процесса (движения), обусловленного внешним воздействием.
По аналогии с теорией линейных САУ введены понятия невозмущённого и возмущённого движения системы. Первое из этих понятий соответствует некоторому частному решению, а второе совокупности иных возможных (общих) решений. Под невозмущённым движением САУ понимают одно из возможных расчётных движений системы при некоторых определённых НУ и заданном внешнем воздействии. Всякое другое движение называют возмущённым. Состояние равновесия и установившийся режим автоколебаний рассматривают как частные случаи невозмущённых движений автономной САУ.
Уравнение динамики автономной САУ п-го порядка при отсутствии возмущающих воздействий записывают в форме Коши
![]() ,
(2.1)
,
(2.1)
где i=1,2,…,n.
Кроме того,![]() обозначает невозмущённое , а
обозначает невозмущённое , а
![]() - возмущённое движение САУ. Отклонения
(вариации) возмущённого движения от
невозмущенного
- возмущённое движение САУ. Отклонения
(вариации) возмущённого движения от
невозмущенного
![]() (2.2)
(2.2)
являются функциями времени и играют существенную роль в исследовании устойчивости. Если
![]() ,
(2.3)
,
(2.3)
то невозмущённое движение называют асимптотически устойчивым.
При исследовании устойчивости САУ часто дифференцальное уравнение (2.1) с учётом (2.2) записывают в форме уравнения возмущённого движения в отклонениях (вариациях)
![]() (2.4)
(2.4)
Переменные (вариации)
![]() являются координатами состояния САУ.
Если
являются координатами состояния САУ.
Если
![]() ,
движение является невозмущённым.
Геометрически невозмущённое
(установившееся) движение
САУ п-го порядка можно представить
условно в виде некоторой интегральной
кривой в п-мерном пространстве с
добавленной осью времени t
(рис.2.1). Возмущённое движение
,
вызванное начальным отклонением
,
движение является невозмущённым.
Геометрически невозмущённое
(установившееся) движение
САУ п-го порядка можно представить
условно в виде некоторой интегральной
кривой в п-мерном пространстве с
добавленной осью времени t
(рис.2.1). Возмущённое движение
,
вызванное начальным отклонением
![]() при
при
![]() ,
изобразиться другой интегральной кривой
(рис.2.1.) .
,
изобразиться другой интегральной кривой
(рис.2.1.) .
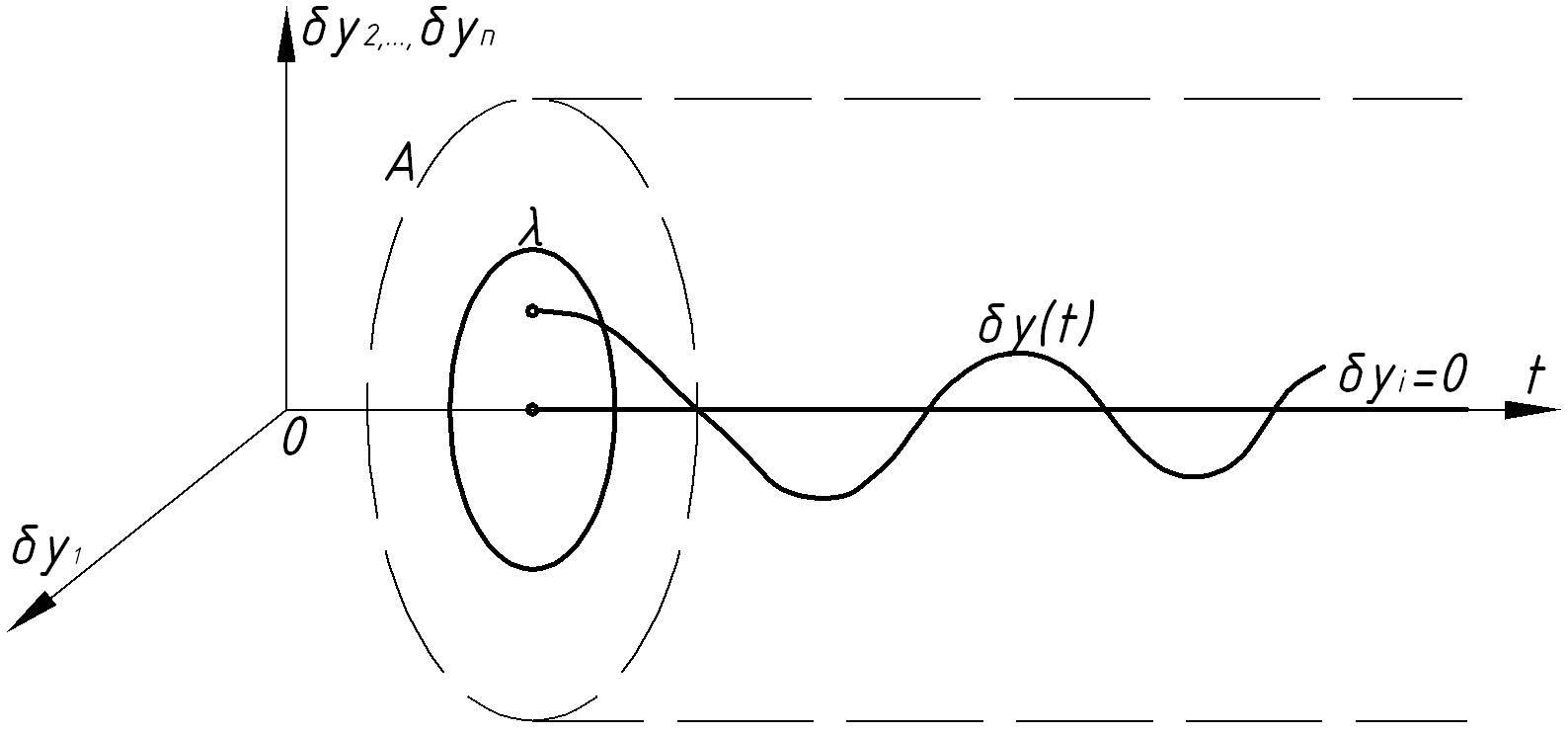
В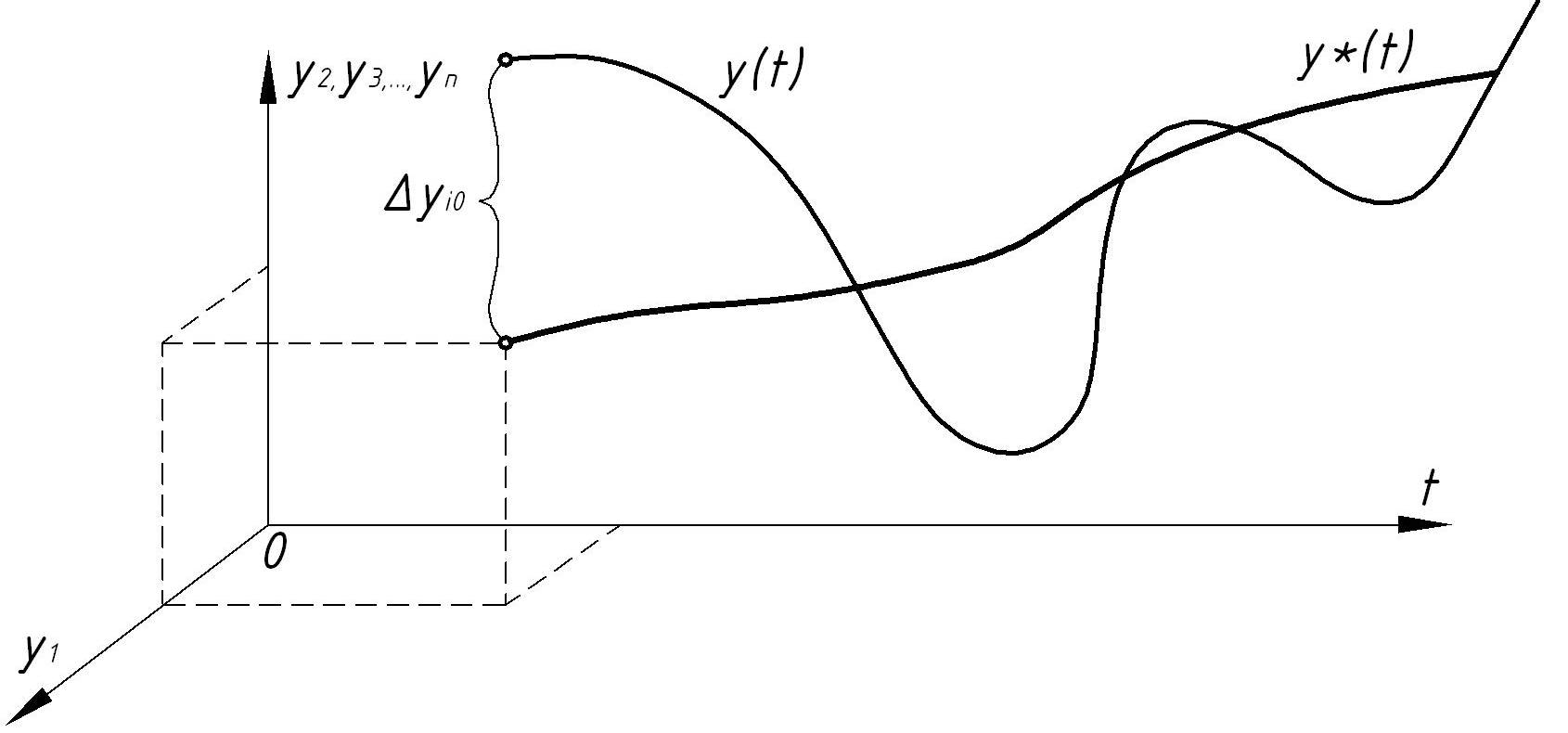 отклонениях
отклонениях
![]() ,
т.е. в пространстве координат состояния
системы, эта картина возмущённого
движения показана на рис.2.2. Невозмущённое
движение
изображено прямой линией, совпадающей
с осью времени t.
,
т.е. в пространстве координат состояния
системы, эта картина возмущённого
движения показана на рис.2.2. Невозмущённое
движение
изображено прямой линией, совпадающей
с осью времени t.
 В зависимости от областей возможных
начальных отклонений от состояния
равновесия САУ в
В зависимости от областей возможных
начальных отклонений от состояния
равновесия САУ в
Рисунок 2.1 теории устойчивости нелинейных систем управления введены понятия устойчивости в малом, в большом и в целом. Система устойчива в малом, если установлено существование области устойчивости, но не определены ее границы. САУ называют устойчивой в большом, когда определены границы области устойчивости, т.е. установлены границы области начальных
Рисунок 2.2 отклонений выходной величины , при которых система возвращается в исходное состояние. В том случае, когда САУ возвращается в исходный режим при любых начальных отклонениях, систему называют устойчивой в целом. Устойчивость в целом для определенного класса нелинейных статических характеристик называют абсолютной устойчивостью.
