Лекции по ТОЭ / ЛЕКЦИЯ8

2.2.1 Простые колебательные контуры

Резонансом называют такое состояние электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и приложенным напряжением равен нулю. Цепи, в которых возникает явление резонанса, называют колебательными контурами, или резонансными цепями.

Резонансные цепи являются составной частью многих устройств: избирательные цепи, частотно-зависимые элементы автогенераторов, фильтров, других аналоговых устройств. Для получения высоких технико-экономических показателей (избирательности, полосы пропускания, коэффициента прямоугольности, равномерности и т. д.) резонансные цепи должны иметь достаточно сложную структуру (многоконтурные связанные цепи, активные резонансные системы и др.).

Простейший колебательный контур содержит индуктивный и ёмкостной элементы, соединенные последовательно (последовательный контур) или параллельно (параллельный контур). Различают два типа резонансов: напряжений и токов. В последовательном контуре возникает резонанс напряжении, а в параллельном — резонанс токов. Частоту, на которой наблюдается явление резонанса, называют резонансной.

2.2.2 Последовательный колебательный контур и резонанс напряжений

На рисунке 8.1 изображена схема последовательного контура с реактивными элементами L и С и активным сопротивлением R, характеризующим потери в контуре.

Рисунок 8.1 - Последовательный колебательный контур

Приложим к контуру гармоническое напряжение с частотой . Комплексное входное сопротивление контура на данной частоте определяется согласно уравнению:

= R + jX = R + j( L - 1/ C), (1)

а ток в контуре уравнением = //(R + jX).

Фазовый сдвиг между током и приложенным напряжением

 = arctg 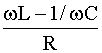= arctg X/R . (2)

При резонансе  = 0, что возможно, если X =  L - (1/ C) = 0. Отсюда получаем уравнение резонансной частоты ₀:

 = ₀ = . (3)

На резонансной частоте комплексное сопротивление носит чисто активный характер, т. е. = R, ток совпадает по фазе с приложенным напряжением и достигает максимального значения . Реактивные сопротивления контура на резонансной частоте ₀ будут равны друг другу:

X_L0 = X_C0 = ₀L = 1/(₀C) = =  . (4)

Величина  носит название волнового (характеристического) сопротивления контура. Резонансные свойства контура характеризуются добротностью контура: Q =  /R.

Величина Q безразмерна и обычно колеблется для реальных контуров от 10 до 100 и выше. Для выяснения физического смысла параметра Q найдем отношение действующих значений напряжений на реактивных элементах (L и С) к действующему значению приложенного напряжения при резонансе:

U_L0/U = U_C0/U = (I₀w₀L)/U = I₀/(₀CU) = /R = Q . (5)

Таким образом, добротность Q показывает, во сколько раз резонансные напряжения на реактивных элементах превышают приложенное напряжение. Отсюда следует и термин “резонанс напряжений”. Энергия источника расходуется только на покрытие тепловых потерь в элементе активного сопротивления R; реактивная мощность при резонансе не потребляется.

2.2.3 Частотные характеристики и полоса пропускания последовательного колебательного контура

Анализируя характер уравнений напряжений и токов в RLC-цепи, фазовых сдвигов между ними при гармоническом воздействии, видно, что они являются частотно-зависимыми. Эта зависимость вытекает непосредственно из зависимости сопротивлений реактивных элементов Х_L и Х_C от частоты . На рисунке 8.2 изображены зависимости Х_L(), Х_C(), Z(),  (), определяемые формулами:

Х_L() = L; Х_C() = 1/(C); Х() = L - 1/C; (6)

Z() = , (7)

 () = arctg{[L - 1/(C)]/R}. (8)

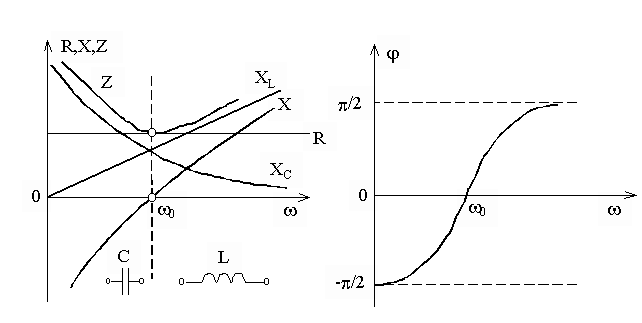
Рисунок 8.2 - Зависимость сопротивлений и фазы от частоты в последовательном колебательном контуре

Зависимости Х_L(), Х_C(), X(), Z() носят название частотных характеристик параметров цепи, а зависимость  () - фазо-частотной характеристики (ФЧХ).

Из представленных характеристик следует, что при  < ₀ цепь имеет емкостной характер (Х<0; <0) и ток опережает по фазе приложенное напряжение; при  > ₀ характер цепи индуктивный (X>0; >0) и ток отстает по фазе от приложенного напряжения; при  = ₀ наступает резонанс напряжений (X=0; =0) и ток совпадает по фазе с приложенным напряжением. Полное сопротивление цепи принимает при этом минимальное значение Z = R.

Зависимость действующего значения тока от частоты можно найти:

. (9)

Действующие значения напряжений на реактивных элементах можно найти согласно закону Ома:

U_L() = I()X_L() = . (10)

U_C() = I()X_C() = . (11)

Зависимости I(), U_L(), U_C() называются амплитудно-частотными характеристиками (АЧХ) относительно тока и напряжений, или резонансными характеристиками, (рисунок 8.3).

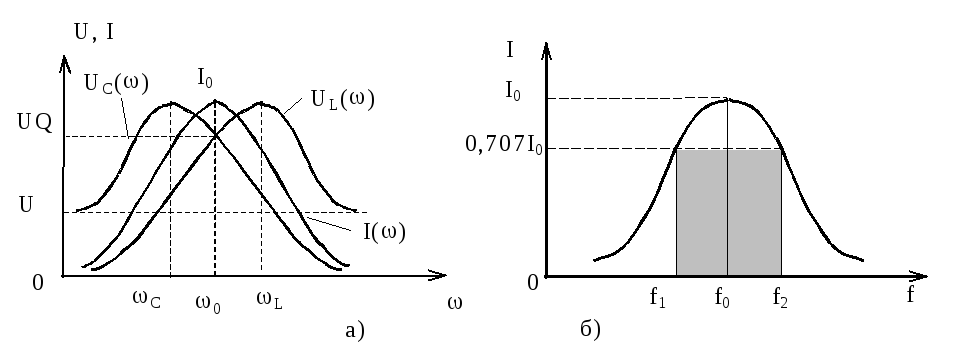
Рисунок 8.3 - АЧХ и полоса пропускания последовательного колебательного контура

Анализ зависимости I( ) показывает, что она достигает максимума при резонансе  = ₀: I₀ = U/R. Зависимости U_L() и U_C() также носят экстремальный характер, причем при  = : (X_L =  ) и U_L( ) = U;

при  = ₀ имеем:

U_L(₀) = U_L0 = U_C0 = I₀r = UQ. (12)

Важной характеристикой колебательного контура является полоса пропускания. Полосой пропускания принято называть полосу частот вблизи резонанса, на границе которой ток снижается в раз относительно I₀ (рисунок 8.3). Абсолютная полоса пропускания  f_A определяется как разность граничных частот f₂ и f₁:

 f_A = f₂ - f₁ = f₀/Q; (13)

Уравнение (13) может быть положено в основу экспериментального определения добротности по АЧХ. Чем выше добротность Q, тем меньше полоса пропускания и наоборот. Причем, поскольку с увеличением потерь R добротность контура падает, то подключение к контуру сопротивления нагрузки или источника с внутренним сопротивлением приводит к расширению полосы пропускания.

 

Параллельный колебательный контур и его свойства