Лекции по ТОЭ / ЛЕКЦИЯ2

1.2.1 Законы Кирхгофа

 Законы Кирхгофа являются основными в теории цепей. Первый закон - закон токов Кирхгофа (ЗТК) формулируется по отношению к узлам электрической цепи и отражает тот факт, что в узлах не могут накапливаться заряды. Он гласит: алгебраическая сумма токов ветвей, сходящихся в любом узле электрической цепи, равна нулю. Формально это записывается так:

, (2.1)

где m - число ветвей, сходящихся в узле.

В этом уравнении токи, одинаково ориентированные относительно узла, имеют одинаковые знаки. Например, знаки выходящих токов можно считать положительными, а входящих - отрицательными. Число независимых уравнений, составляемых по ЗТК, равно числу независимых узлов электрической цепи.

Второй закон - закон напряжений Кирхгофа (ЗНК) формулируется по отношению к контурам и гласит: алгебраическая сумма напряжении ветвей в любом контуре цепи равна нулю.

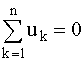, (2.2)

где n - число ветвей, входящих в контур.

В этом уравнении напряжения, совпадающие с направлением обхода контура, записываются со знаком "+", а не совпадающие - со знаком "-".

Иллюстрация законов Кирхгофа

Рассмотрим пример, в котором рассчитываются токи ветвей схемы резистивной цепи, изображенной на рис. 2.1, по методу уравнений Кирхгофа. Схема имеет n_у = 4 узла, n_в = 6 ветвей. Выберем узел 4 в качестве базисного и составим n_у - 1 = 3 уравнения по ЗТК: для 1-го узла -i₁ + i₃ + i₄ = 0; для 2-го узла -i₂ - i₃ + i₅ = 0; для 3-го узла i₂ - i₄ + i₆ = 0. По ЗНК составляем n_в - n_у + 1 = 3 уравнения для контуров, показанных на рисунке стрелками: для 1-го контура -u_г1 + u₁ + u₃ + u₅ = 0; для 2-го контура u_г2 + u₂ - u₃ + u₄ = 0; для 3-го контура -u_г2 - u₂ + u₆ - u₅ = 0. Или с учетом закона Ома:

Рисунок 2.1 - Схема, отражающая применение ЗТК и ЗНК

-u_г1 +R₁i₁ + R₃i₃ + R₅i₅ = 0 ;

u_г2 + R₂i₂ - R₃i₃ + R₄i₄ = 0 ;

-u_г2 -R₂i₂ + R₆i₆ - R₅i₅ = 0 .

Решая совместно эти системы уравнений, находят искомые токи.

1.2.2 Преобразование электрических схем

Преобразования электрических схем применяются для упрощения расчетов. Наиболее типичные методы преобразования следующие.

Последовательное соединение элементов. Согласно ЗТК при последовательном соединении элементов через них протекает один и тот же ток (рисунок 2.2).

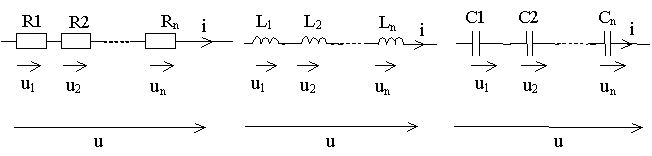
Рисунок 2.2 - Последовательное соединение элементов

Согласно ЗНК напряжение, приложенное ко всей цепи:

. (2.3)

Тогда для последовательного соединения резистивных элементов R₁, R₂, ..., R_n будем иметь:

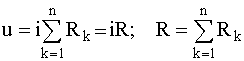. (2.4)

Для последовательного соединения индуктивных элементов (рисунок 2.2):

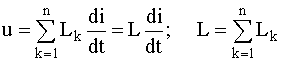. (2.5)

Для последовательного соединения емкостных элементов:

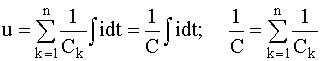. (2.6)

Таким образом, цепь из n последовательно соединенных резистивных, индуктивных или емкостных элементов может быть заменена одним эквивалентным резистивным, индуктивным или емкостным элементом. Причем при нахождении эквивалентного сопротивления или эквивалентной индуктивности необходимо суммировать сопротивления и индуктивности отдельных резистивных и индуктивных элементов, а для нахождения эквивалентной обратной емкости - суммировать величины, обратные емкости отдельных емкостных элементов. При n = 2:

С = С₁C₂/(С₁ + С₂). (2.7)

При последовательном соединении независимых источников напряжения они заменяются одним эквивалентным источником напряжения с задающим напряжением u_г, равным алгебраической сумме задающих напряжений отдельных источников. Причем со знаком “+” берутся задающие напряжения совпадающие с задающим напряжением эквивалентного источника, а со знаком “-” - несовпадающие (рисунок 2.3).

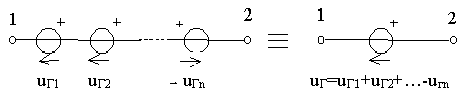
Рисунок 2.3 - Последовательное соединение источников напряжения

Параллельное соединение элементов. При параллельном соединении элементов согласно ЗНК к ним будет приложено одно и то же напряжение (рисунок 2.4). Согласно ЗТК для тока каждой из схем, изображенных на рисунке 2.4, можно записать:

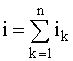. (2.8)

Рисунок 2.4 - Параллельное соединение пассивных элементов

На основании этого уравнения для параллельного соединения резистивных элементов получаем:

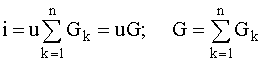. (2.9)

Для параллельного соединения емкостных элементов:

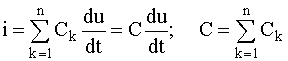. (2.10)

Для параллельного соединения индуктивных элементов:

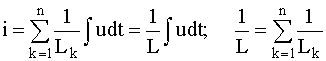. (2.11)

Следовательно, цепь из n параллельно соединенных резистивных, индуктивных или емкостных элементов можно заменить одним эквивалентным резистивным, индуктивным или емкостным элементом.

Таким образом, при параллельном соединении резистивных, емкостных и индуктивных элементов для нахождения эквивалентных проводимости и емкости цепи проводимости или емкости отдельных элементов складываются. Эквивалентная обратная индуктивность цепи находится суммированием обратных индуктивностей отдельных индуктивных элементов. В частности, при n = 2:

R = R₁R₂/(R₁ + R₂); L = L₁L₂/(L₁ + L₂) . (2.12)

Параллельно соединенные независимые источники тока можно заменить одним эквивалентным источником тока с задающим током, равным алгебраической сумме задающих токов отдельных источников. Причем со знаком “+” берутся задающие токи, совпадающие по направлению с задающим током эквивалентного источника, а со знаком “-” - не совпадающие (рисунок 2.5).

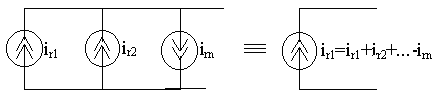
Рисунок 2.5 - Параллельное соединение источников тока

При расчете электрических цепей часто возникает необходимость преобразования источника напряжения с параметрами u_г и R_г, в эквивалентный источник тока с параметрами i_г и G_г, или наоборот - преобразование источника тока в эквивалентный источник напряжения. Эти преобразования осуществляются в соответствии с формулами

i_г = u_г/R_г ; G_г = 1/R_г . (2.13)

Пример преобразования “звезда—треугольник”. Кроме последовательного и параллельного соединений элементов весьма распространенными являются соединения элементов треугольником и звездой (рисунок 2.6).

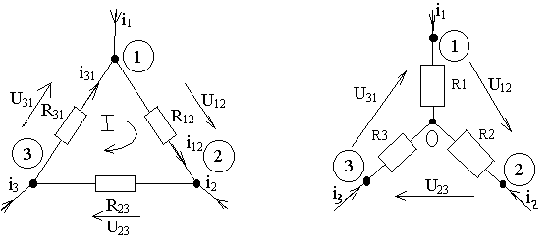
Рисунок 2.6 - Соединения треугольником и звездой

Существуют формулы преобразования соединения треугольника в звезду:

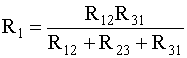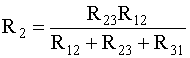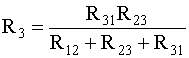; ; . (2.14)

Обратный переход можно получить по формулам, которые получены из предыдущих:

R₁₂ = R₁ + R₂ + R₁R₂/R₃ ; R₂₃ = R₂ + R₃ + R₂R₃/R₁ ; R₃₁ = R₃ + R₁ + R₃R₁/R₂ . (2.15)

Аналогично существуют формулы преобразования “звезда—треугольник” индуктивных и емкостных элементов [1, с. 23-24].

1.2.3 Принцип наложения

Принцип наложения (суперпозиции) имеет важнейшее значение в теории линейных электрических цепей. Подавляющее число методов анализа линейных цепей базируется на этом принципе. Если рассматривать напряжения и токи источников как задающие воздействия, а напряжение и токи в отдельных ветвях цепи как реакцию (отклик) цепи на эти воздействия, то принцип наложения можно сформулировать следующим образом: реакция линейной цепи на сумму воздействий равна сумме реакций от каждого воздействия в отдельности.

Принцип наложения можно использовать для нахождения реакции в линейной цепи, находящейся как под воздействием нескольких источников, так и при сложном произвольном воздействии одного источника.

Рассмотрим случай, когда в линейной цепи действует несколько источников. В соответствии с принципом наложения для нахождения тока i или напряжения u в заданной ветви осуществим поочередное воздействие каждым источником и найдем соответствующие частные реакции i_k и u_k на эти воздействия. Тогда результирующая реакция определится как

, (2.16)

где n - общее число источников.

Проиллюстрируем принцип наложения (суперпозиции) на примере резистивной цепи, изображенной на рисунке 2.7, а.

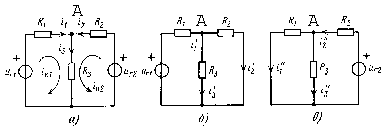
Рисунок 2.7 - Иллюстрация принципа суперпозиции

Найдем ток в резистивном элементе R₃. Положим вначале, что в цепи действует только один источник u_г1: второй источник напряжения исключается и зажимы его закорачиваются. При этом получаем частичную схему, изображенную на рисунке 2.7,б. Определим ток i₃^' от воздействия напряжения u_г1, учитывая, что и :

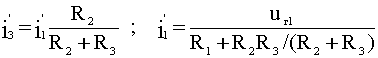. (2.17)

Теперь полагаем, что в цепи действует только источник u_г2. Исключив источник u_г1, получим вторую частичную схему. Ток i₃^'' от воздействия u_г2 определится как, учитывая, что и :

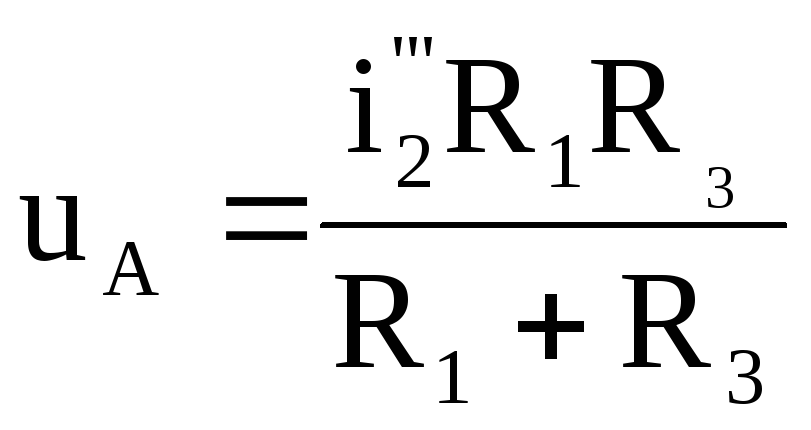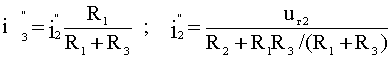. (2.18)

Результирующий ток i₃ найдем как алгебраическую сумму частных токов: i₃ = i₃^' + i₃^'' . При определении результирующих токов знак “+” берут у частных токов, совпадающих с выбранным положительным направлением результирующего тока, и знак “—” - у несовпадающих. Как следует из рассмотренного примера, при составлении частичных электрических схем исключаемые идеальные источники напряжения закорачиваются. В случае, если в цепи действуют источники напряжения с внутренними сопротивлениями R_г, при их исключении они заменяются своими внутренними сопротивлениями R_г.

При наличии идеальных источников тока соответствующие ветви исключаемых источников размыкаются, а при наличии реальных источников они заменяются своими внутренними проводимостями G_г.

Если в линейной цепи приложено напряжение сложной формы, применение принципа наложения позволяет разложить это воздействие на сумму простейших и найти реакцию цепи на каждое из них в отдельности с последующим наложением полученных результатов.

Методы контурных токов, узловых напряжений и эквивалентного генератора