§9. Аксонометрия. Изображение точек.

Пусть R ; ¯ = {O; ¯, E1;¯, E2;¯, E3;¯} – аффинный репер в пространстве. Пусть e1;\s\up8(( = \O(O; ¯, e2;\s\up8(( = \O(O; ¯, e3;\s\up8(( = \O(O; ¯. Пусть M; ¯ – произвольная точка в пространстве с координатами (x₁, x₂, x₃). Это означает, что

\O(O; ¯= x₁e1;\s\up8(( + x₂e2;\s\up8(( + x₃e3;\s\up8(( .

П усть M3;¯ – проекция точки M; ¯ на координатную плоскость O; ¯E1;¯E2;¯ параллельно вектору e3;\s\up8(( , а Mo;¯ – проекция точки M3;¯ на ось Ox параллельно вектору e2;\s\up8(( . Тогда ломаная O; ¯Mo;¯M3;¯M; ¯ называется координатной ломаной точки M; ¯. Для её звеньев выполнено

|O; ¯Mo;¯|=|x₁||O; ¯E1;¯|, |Mo;¯M3;¯|=|x₂||O; ¯E2;¯|,

|O; ¯Mo;¯|=|x₃||O; ¯|.

В ыберем плоскость изображений  и направление проецирования не параллельно координатным плоскостям. Спроецируем на плоскость репер вместе с координатной ломаной и применим преобразование подобия. Получим изображение R = {O, E₁, E₂, E₃} аффинного репера и изображение OM_oM₃M координатной ломаной. При аффинном отображении сохраняется соотношение отрезков, принадлежащих параллельным прямым. Поэтому и на изображении выполняется

|OM_o|=|x₁||OE₁|, |M_oM₃|=|x₂||OE₂|, |M₃M|=|x₃||OE₃|.

Из этого вытекает следующее утверждение.

Если на плоскости  дано изображение аффинного репера, то мы можем построить изображение M данной точки M; ¯ по её координатам. Если даны изображения аффинного репера и координатной ломаной, то мы можем определить координаты точки M; ¯.

Заметим, что само изображение M точки не M; ¯ даёт возможности найти координаты этой точки. Если даны на изображении две точки M и M₃, то мы можем восстановить изображение всей координатной ломаной, и тем самым, найти координаты M; ¯.

Если мы умеем строить изображения точек в системе координат, то мы можем строить и изображение пространственных фигур. Этот метод называется методом аксонометрического проецирования. Точку называют началом аксонометрической СК, а оси OE₁, OE₂, OE₃ – аксонометрическими осями.

П усть M1;¯, M2;¯ – проекции точки M на координатные плоскости O; ¯E3;¯ и O; ¯E1;¯E3;¯ соответственно параллельно координатным осям O; ¯E1;¯ и O; ¯E2;¯. Пусть M₁, M₂ – изображения этих точек. Тогда точка M называется аксонометрической проекцией точки M; ¯, а M₁, M₂, M₃ называются её вторичными проекциями. Для того, чтобы определить координаты точки M; ¯ по её изображению, достаточно иметь на чертеже её аксонометрическую проекцию и любую из вторичных. Но, если не оговорено, о какой вторичной проекции идёт речь, то предполагается, что это точка M₃.

Вместо утверждения «в пространстве дана точка M; ¯, аксонометрическая проекция которой есть M, а вторичная M₃» будем говорить «дана точка (M, M₃)».

§10. Изображение прямых и плоскостей в аксонометрической проекции.

Б удем предполагать, что направление проецирования не параллельно рассматриваемым прямым и плоскостям. Тогда изображением прямой будет прямая, а изображение плоскости будет накрывать всю плоскость .

П рямая a;¯ на плоскости изображений  задаётся двумя своими точками (M, M₃) и (N, N₃) или аксонометрической проекцией a и вторичной a₃. Тогда говорим, что дана прямая (MN, M₃N₃) или прямая (a, a₃). Если прямая a;¯ не параллельна оси O; ¯E3;¯, то её вторичная проекция есть прямая. Если a;¯ ||O; ¯E3;¯, то её вторичная проекция есть точка. В последнем случае, мы подписываем эту точку всё равно, как a₃. Сама ось O; ¯E3;¯ задаётся на изображении как (OE₃, O). Если прямая b;¯ лежит в плоскости O; ¯E1;¯E2;¯, то её аксонометрическая и вторичная проекции совпадают: b=b₃.

Рассмотрим возможные варианты расположения двух прямых (a, a₃) и (b, b₃). Как у параллельных прямых, так и у пересекающихся, могут совпадать либо аксонометрические, либо вторичные проекции. Если совпадают и те и другие, то совпадают и сами прямые.

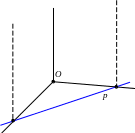
Плоскость может быть задана тремя своими точками, либо двумя своими прямыми, либо прямой и не лежащей на ней точкой. Пусть p;¯ – прямая, по которой данная плоскость (;¯ пересекает координатную плоскость O; ¯E1;¯E2;¯, а p – её изображение. Тогда прямая p называется следом плоскости. Пусть P; ¯ – точка пересечения

п лоскости (;¯ с координатной осью O; ¯E3;¯, (P, O) – её изображение. Наиболее удобным считается способ изображения плоскости именно с помощью этих элементов: следа p и точки (P, O). Можно также говорить о следах данной плоскости на других координатных плоскостях O; ¯E1;¯E3;¯ и O; ¯E2;¯E3;¯; на чертеже они изображены пунктиром. Но если не сказано, о каком следе идёт речь, то предполагается, что это след на плоскости O; ¯E1;¯E2;¯.

В озможны варианты расположения плоскости, при которых один из вышеупомянутых элементов отсутствует.

П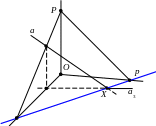 усть прямая a;¯ пересекает координатную плоскость O; ¯E1;¯E2;¯ в точке X; ¯. Аксонометрическая и вторичная проекции этой точки совпадают – это точка X. Точка X называется следом прямой a;¯. Если прямая a;¯ параллельна O; ¯E1;¯E2;¯, то след у неё будет отсутствовать. Можно также говорить о следах прямой на других координатных плоскостях. Если говорится просто «след прямой», то подразумевается, что след на плоскости O; ¯E1;¯E2;¯.

Ключом к решению многих задач на построение является следующее очевидное утверждение. Если прямая лежит на плоскости, то её след лежит на следе плоскости.