§ 8. Изображение цилиндра и конуса.

1. Пусть цилиндр-оригинал F; ¯ расположен так, что его ось O; ¯O1;¯ параллельна плоскости изображений . Направление прое­цирования выберем следующим образом. Через ось цилиндра проведём плоскость  и выберем направление проецирования параллельно этой плоскости, но не параллельно основаниям цилиндра (иначе изображение будет выглядеть, как прямоугольник, и не будет наглядным).

П усть (;¯ – окружность верхнего основания цилиндра, A; ¯B; ¯ и C; ¯D; ¯ – взаимно перпендикулярные диаметры этой окружности, причём A; ¯B; ¯ ||, C; ¯D; ¯. Тогда C; ¯D; ¯. Проведём образующие A; ¯A1;¯, B; ¯B1;¯, которые будем называть контурными. Пусть l1;¯ и l2;¯ – касательные к окружности (;¯ в точках A; ¯ и B; ¯. При проецировании окружность (;¯ переходит в эллипс  с осями AB и CD. Отрезок A; ¯A1;¯ и прямая l1;¯ лежат в плоскости, параллельной направлению проецирования, поэтому они проецируются на одну прямую l₁. При этом, прямая l1;¯ была касательной к (;¯. Следовательно, изображение AA₁ контурной образующей лежит на каса­тельной к эллипсу . Аналогично ВВ₁ тоже лежит на касательной к эллипсу .

Дополнительно потребуем, чтобы угол между вектором p;\s\up8(( и осью цилиндра был больше 45. Тогда на изображении будет |AB|>|CD|. Итак, мы окончательно имеем следующее изображение.

2. Выберем плоскость изображения  параллельно оси S; ¯O; ¯ данного конуса (; ¯. Пусть  – плоскость основания конуса, а  – плоскость, проходящая через ось цилиндра, перпендикулярно . Направление прое­цирования выберем следующим образом. Через вершину S; ¯ проведём прямую l;¯ в плоскости , так чтобы она пересекала плоскость  в точке K; ¯, расположенной вне основания конуса, и так чтобы угол между высотой S; ¯O; ¯ и прямой l;¯ был больше 45. Теперь выберем направление проецирования параллельно l;¯.

Пусть (;¯ – окружность основания конуса, A; ¯B; ¯ и C; ¯D; ¯ – взаимно перпендикулярные диаметры этой окружности, причём A; ¯B; ¯ ||, C; ¯D; ¯. Тогда C; ¯D; ¯. Проведём касательные K; ¯M; ¯, K; ¯N; ¯ к (;¯. Образующие S; ¯M; ¯ и S; ¯N; ¯ назовём контурными.

П ри проецировании окружность (;¯ переходит в эллипс  с осями AB и CD. Прямые S; ¯O; ¯ и C; ¯D; ¯ лежат в плоскости  параллельной направлению проецирования, поэтому S; ¯O; ¯ и C; ¯D; ¯ проецируются на одну прямую. Точки S; ¯ и K; ¯ проецируются в одну точку, поэтому проекции отрезков K; ¯M; ¯ и S; ¯M; ¯ совпадают. Значит, изображение SM контурной образующей будет касательной к . Аналогично, SN – тоже касательная. Хорда M; ¯N; ¯ параллельна A; ¯B; ¯. Поэтому и на изображении MN||AB.

Самое главное, что следует уяснить: изображения контурных образующих ни в коем случае не проходят через концы главного диаметра эллипса.

§9. Изображение шара.

Пусть (; ¯ – шар-оригинал. Проведём все возможные касательные к шару параллельные направлению проецирования. Они образуют цилиндрическую поверхность, которая касается шара по большой окружности (;¯. В пересечении цилиндрической поверхности с плоскостью изображений 

п олучится эллипс _o, который называется очертанием шара. Этот эллипс вместе со своей внутренностью будет проекцией шара (обозначаем _o).

Е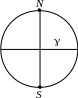 сли направление проецирования p;\s\up8(( не перпендикулярно плоскости изображений , то _o не является окружностью. Не будет окружностью и любая подобная _o фигура. Такое изображение не будет наглядным. Поэтому мы рассмотрим только изображение шара в ортогональной проекции.

Д ля того, чтобы сделать изображение более наглядным, кроме очертания шара рисуют ещё изображение какой-либо большой окружности (;¯ – экватора. Плоскость экватора  не должна быть перпендикулярна плоскости . В противном случае, экватор будет изображаться отрезком, и изображение не будет наглядным. Также принято изображать полюса – концы диаметра шара N; ¯S; ¯, перпендикулярного плоскости экватора.

Изучим, как правильно изображать экватор и полюса. Пусть A; ¯B; ¯ и D; ¯ – взаимно перпендикулярные диаметры экватора, причём A; ¯B; ¯ ||. Пусть A_oB_o и C_oD_o – проекции этих диаметров. Тогда |A_oB_o|=|A; ¯B; ¯ |. Обозначим R; ¯ – радиус шара,  – угол между C; ¯D; ¯ и плос­костью . Тогда

|O_oA_o|=R; ¯,

| O_oC_o|=R; ¯·cos, |O_oN_o|=R; ¯·sin.

Изображение шара подобно его проекции. Поэтому на изображении тоже выполняются соотношения

|OC|=|OA|·cos, |ON|=|OA|·sin. (_*)

Проведём через точку C половину хорды CK, а через точку N – половину хорды NM. В OCK и ONM

|OK|=|OM|=|OA|,

|OC|=|OK|·cosKOC=|OA|·cosKOC.

|ON|=|OM|·sinOMN =|OA|·sinOMN.

Следовательно, KOC=OMN= и треугольники KOC, OMN равны. Поэтому

|KC|=|ON|, |OC|=|NM|. (3)

Итак.

1. Если дано изображение экватора , мы можем однозначно определить, где располагаются точки N и S, изображающие полюсы. Пусть AB – большой диаметр для , CD – малый диаметр. Проведём через точку C половину хорды CK параллельно AB. На перпендикуляре к AB, проходящем через точку O отложим отрезки ON и OS, равные CK.

2. Если дано изображение полюсов N и S, мы можем построить изображение экватора. Большой диаметр изображения экватора – это диаметр очертания шара, перпендикулярный NS. Малый диаметр CD лежит на прямой NS. Проведём через точку N – половину хорды NM. Тогда |OC|=|OD|=|NM|.

Е щё раз подчеркнём, что полюсы лежат на очертании шара тогда и только тогда, когда экватор изображается отрезком.

При построении изображения шара вместе с декартовой СК следует учесть, что оси Ox и Oy должны проходить через сопряжённые диаметры экватора, а ось Oz – через полюс. Если у нас уже изображена ось Ox, мы проводим вспомогательную хорду изображения экватора, параллельную Ox, и через середину хорды должна проходить Oy.