§14. Построение сечений многогранников. Метод следов.

В этом методе мы первым действием (после нахождения вторичных проекций данных точек) строим след секущей плоскости на плоскости верхнего или нижнего основания призмы или усечённой пирамиды или на основании пирамиды. В качестве примеров мы рассмотрим те же задачи.

Задача 2. Решение. Мы уже имеем одну точку на верхнем основании призмы, поэтому и след мы будем строить на верхнем основании. Строим вторичные проекции точек N и P на верхнее основание. Затем:

1. NPN₃P₃=X;

2. MX=p – след;

3. pB₁C₁=D.

Дальнейшие действия уже были показаны выше на чертеже.

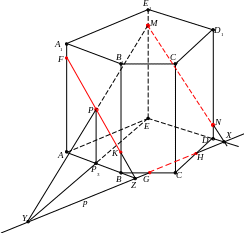
Задача 3. Решение. Мы будем строить след секущей плоскости на нижнем основании призмы.

Строим:

1. MNED=X, MPEP₃=Y;

2. p=XY – след;

3. pBC=G, pDC=H.

Найденных точек G и H недостаточно, чтобы завер­шить построение.

Нам нужно найти точку на ребре BB₁ или на ребре AA₁.

В грани ABB₁A₁ мы уже имеем одну точку P. Поэтому нижнее ребро этой грани, т.е. AB, мы продолжаем до пересечения со следом. Эти две линии должны пересечься, т.к. они лежат в одной плоскости:

4. ABp=Z.

Точки P и Z лежат одновременно в плоскости одной грани и в секущей плоскости. Поэтому они лежат на линии пересечения плоскостей. Строим:

5. PZAA₁=F; PZBB₁=K.

Дальнейшие действия уже показаны выше.

Если вдруг окажется, что линия AB не пересекается со следом, то искомая линия FK тоже будет параллельна следу.

Недостаток метода следов заключается в том, что построение зачастую далеко уходит за пределы чертежа и не помещается на лист бумаги. В методе соответствия все построения совершаются в пределах изображения фигуры.

З адача 4. Решение.

1. PNP_oN_o=X;

2. MNCN_o=Y;

3. p=XY – след;

3. CBp=Z;

4. ZMSB=E;

5. ENSA=G

6. GEMF – искомое сечение.

Для тех, кто до сих пор не запомнил процесс построения, попробуем записать его ещё раз словами.

Выбираем любые две заданные точки и соединяем их. Получается первая прямая. Соединяем вторичные проекции

э тих точек. Получается вторая прямая. В пересечении этих прямых получается точка, лежащая на следе. Затем мы берём другую пару заданных точек и находим вторую точку на следе. Мы соединяем найденные точки на следе и получаем след секущей плоскости. Затем, мы продолжаем до пересечения со следом любое нижнее ребро, лежащее в грани, где есть данная точка и найденную точку можем соединить с заданной точкой.

При построении сечений призмы и усечённой пирамиды иногда бывает полезно использовать следующий факт: следы секущей плоскости на нижнем и на верхнем основании параллельны. Случай усечённой пирамиды мы рассмотрим на практических занятиях. Для того, чтобы проде­монстрировать данный приём на примере, мы немного изменим данные в задаче 3. Точка F оказывается не на ребре AA₁, а на ребре A₁B₁. Далее мы проводим прямую p₁||p через F и находим точку L на ребре A₁E₁. Остаётся соединить между собой все найденные

вершины сечения.