Волны. Волновые процессы

1. Волны. Волновое уравнение

Понятие волны. Как происходит распространение колебаний – передача воздействия от источника к приемнику. Как доходят до нашего уха колебания давления воздуха, возникающие около звучащего камертона? Каким образом свет, испускаемый звездами, достигает нашего глаза?

Для рассмотрения подобного рода вопросов необходимо ввести новое физическое понятие – волны. В физике волнами или волной называют всякое изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например плотности вещества, напряженности электрического поля, температуры.

Волной часто называют также всякое явление, при котором в пространстве происходит распространение кратковременного электрического или механического «толчка». Таким образом, понятие «волна» охватывает обширный круг явлений.

Замечание. Когда речь идет о волнах на поверхности воды, волной (в единственном числе) называют обычно совокупность одного горба и одной смежной с ним впадины. Когда говорят (также в единственном числе) «звуковая (или электромагнитная) волна такой-то частоты», всегда имеют в виду бесконечную вереницу «горбов» и «впадин».

Волновое уравнение. Рассмотрим произвольную функцию

(6.1)

от аргумента . Продифференцируем ее дважды по времени :

,

. (6.2)

Здесь штрих означает дифференцирование по аргументу . Теперь продифференцируем нашу функцию дважды по координате :

. (6.3)

Сравнивая (6.2) и (6.3), убеждаемся, что функция (6.1) удовлетворяет уравнению

или , (6.4)

в котором – фазовая скорость волны. Легко видеть, что этому же уравнению удовлетворяет произвольная функция аргумента :

(6.5)

а также сумма функций вида (6.1) и (6.5).

Дифференциальное уравнение в частных производных (6.4) называется волновым уравнением. При положительных значениях функции (6.1) и (6.5) изображают плоские волны, распространяющиеся, не деформируясь, со скоростью в сторону соответственно возрастающих или убывающих значений .

Плоская монохроматическая волна. Волновой вектор. Особый интерес представляет частный случай, когда функция синусоидальна:

. (6.6)

В каждой точке пространства, где значение фиксировано, величина совершает гармоническое колебание. Его амплитуда равна , а круговая частота равна . Обе эти величины одинаковы для всех . Фаза колебания равна . Она различна для различных и пропорциональна расстоянию от плоскости . Коэффициент пропорциональности между фазой и расстоянием называется волновым числом. При положительных значениях выражение (6.6) описывает волну, распространяющуюся в сторону возрастающих (слева направо), а выражение

(6.6а)

– волну, распространяющуюся в сторону убывающих значений (справа налево).

Моментальный снимок волны (6.6) – график зависимости при фиксированном значении – есть синусоида в пространстве. Например, в момент времени .

Пространственный период такой, что при любом , называют длиной волны. Длина волны равна тому пути, который проходит волна за один период колебаний. Длина волны связана с волновым числом соотношением (ср. соотношение, связывающее и ): , откуда

. (6.7)

Физический смысл волнового вектора: величина дает число волн, укладывающихся в (густоту волн), следовательно, – это число «кусочков» волны, укладывающихся в . Каждый «кусочек» в раз меньше длины волны. В оптике часто называют волновым вектором величину .

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Фазовая скорость волны – это скорость, с которой распространяется фаза колебания, равна:

, (6.8)

где - период колебания. Формула (6.6) может быть также записана в виде:

. (6.9)

Из такой записи сразу видно, что колебание в плоскости воспроизводит колебания в плоскости с опозданием на секунд.

6.2.4. Стоячие волны. Пусть скалярная величина зависит от координат рассматриваемой точки и времени следующим образом:

, (6.10)

где – некоторая однозначная функция, и – постоянные. Это значит, что величина во всех точках пространства совершает гармоническое колебание с одинаковой частотой и фазой, но амплитуда колебания различна для различных точек пространства. Такое явление называется стоячей волной. Волну (6.6) для того, чтобы подчеркнуть ее отличие от стоячей волны, называют бегущей волной.

Для частного случая плоской стоячей волны амплитуда зависит только от одной координаты, скажем :

. (6.11)

Интерес представляет случай, когда , т. е.

, (6.12)

где - постоянные, т. е. когда распределение амплитуды в пространстве синусоидально. Такая стоячая волна называется синусоидальной стоячей волной.

Докажем, что суперпозиция двух бегущих плоских синусоидальных волн одинаковой амплитуды и частоты, распространяющихся в противоположных направлениях, есть стоячая плоская синусоидальная волна.

В самом деле, пусть . Тогда .

Воспользуемся формулой ,

. (6.13)

Это – уравнение стоячей волны.

В точках среды, где

, (6.14)

амплитуда результирующей стоячей волны достигает максимального значения, равного . Она вдвое больше амплитуды каждой из бегущих волн. Эти точки называются пучностями стоячей волны.

В точках среды, где

, (6.15)

амплитуда колебаний падает до нуля. Эти точки все время остаются в покое. Они называются узлами стоячей волны.

Из формул (6.14) и (6.15) следует, что соседние узлы и пучности отстоят на расстоянии полуволны друг от друга.

Таким образом, основное отличие стоячей волны от бегущей заключается в том, что все точки стоячей волны между соседними узлами колеблются с разными амплитудами, но в одной фазе, в то время как все точки бегущей волны совершают колебания с одинаковой амплитудой, но с разными фазами.

Векторные волны. Поляризация. Предположим теперь, что некоторая векторная величина (скорость, напряженность электрического или магнитного поля и т. д.) является функцией координат и времени. Ограничимся случаем плоской недеформирующейся волны: .

Если вектор перпендикулярен к направлению распространения, т. е. к оси , то волна называется поперечной, если параллелен направлению распространения, то волна называется продольной. В общем случае вектор имеет и продольную и поперечную составляющие.

Случай продольной волны мало отличается от случая скалярной волны. Вместо вектора здесь можно рассматривать скаляр: ,

– проекция вектора на ось . Здесь, как и в случае скалярной волны, все направления, перпендикулярные к направлению распространения, физически равноправны между собой.

Частным случаем поперечной волны является тот, когда вектор имеет во всех точках пространства одинаковое и постоянное во времени направление, но, вообще говоря, различный знак (рис. 6.1).

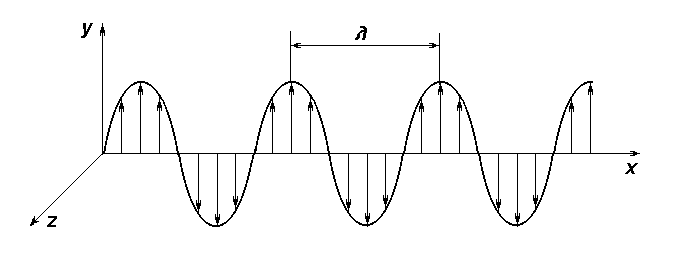
Рис. 6.1. Поперечная волна

Расположим ось по этому направлению. Изменение во времени и пространстве вектора может быть описано заданием, как функции и , скаляра: .

Но этот случай коренным образом отличается от продольной векторной волны. Здесь различные направления, перпендикулярные к направлению распространения, не равноправны между собой (например, направление осей ).

Рассмотрим общий случай поперечной волны, когда не только величина, но и направление вектора зависит от и . Назовем синусоидальной поперечной волной такую, в которой проекции вектора на два взаимно перпендикулярных направления, перпендикулярные к направлению распространения , выражаются формулами:

,

где – постоянные; эти проекции образуют, таким образом, синусоидальные скалярные волны одинаковой частоты, распространяющиеся с одинаковой скоростью. Отсюда следует (см. п. 5.2.5), что конец вектора описывает во всех точках пространства (т. е. при любом фиксированном ), вообще говоря, одинаковые и одинаково ориентированные эллипсы. Это свойство синусоидальной поперечной волны принято выражать словами: синусоидальная поперечная волна, вообще говоря, эллиптически поляризована.