3. Затухающие колебания

3.2. Основные представления

3.2.1. Пренебрежение трением (электрическим сопротивлением) приводит к выводу о незатухающем характере колебаний. Однако из опыта известно, что при достаточно продолжительном наблюдении можно обнаружить постепенное уменьшение амплитуды колебаний вплоть до полного прекращения колебательного движения. Энергия движущегося тела при этом, в конце концов, переходит в тепло или, как говорят, диссипируется.

Пусть трение пропорционально скорости колебаний. Это утверждение представляет собой идеализацию реальных законов трения. Однако когда речь идет о жидком трении или трении о воздух при достаточно малых скоростях, это предположение находится в удовлетворительном соответствии с опытом. Итак, пусть сила трения для системы, совершающей одномерные колебания, равна:

, (3.1)

где – коэффициент трения, учитывающий все: вязкость среды, размеры движущегося тела и т. д. Добавим эту силу в правую часть уравнения (2.1):

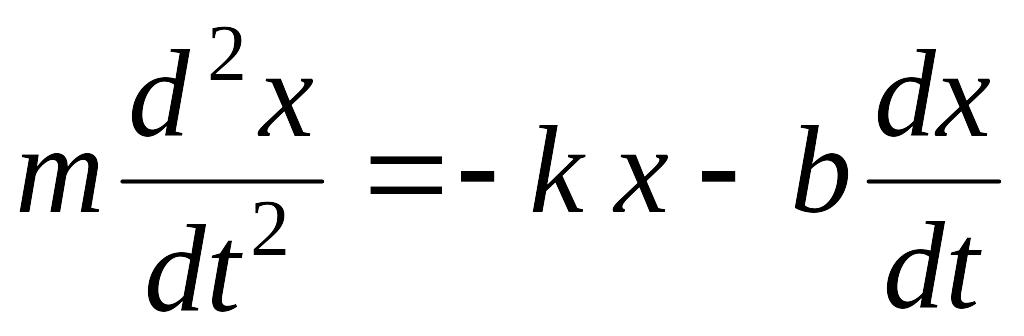. (3.2)

Разделим его на и введем обозначения:

, (3.3)

. (3.4)

где – частота собственных колебаний системы в отсутствие трения. Величина называется коэффициентом затухания и имеет размерность , также как и . Таким образом, имеем уравнение

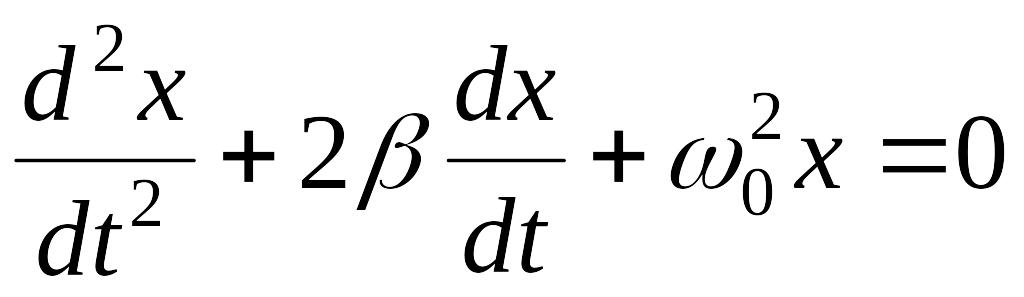. (3.5)

Для его решения введем новую переменную :

. (3.6)

Заготовим и , и подставим их в (3.5):

,

,

.

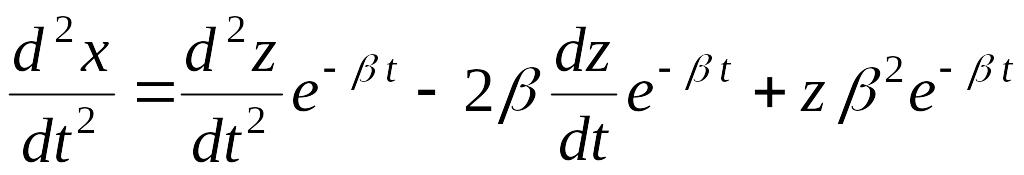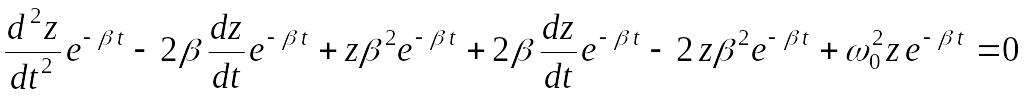После сокращения получим:

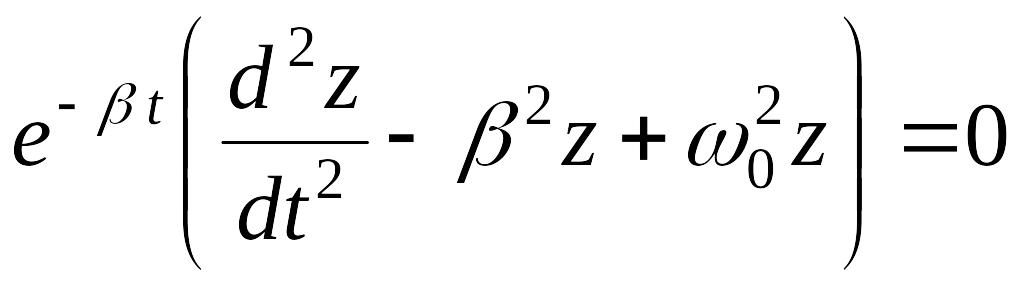и

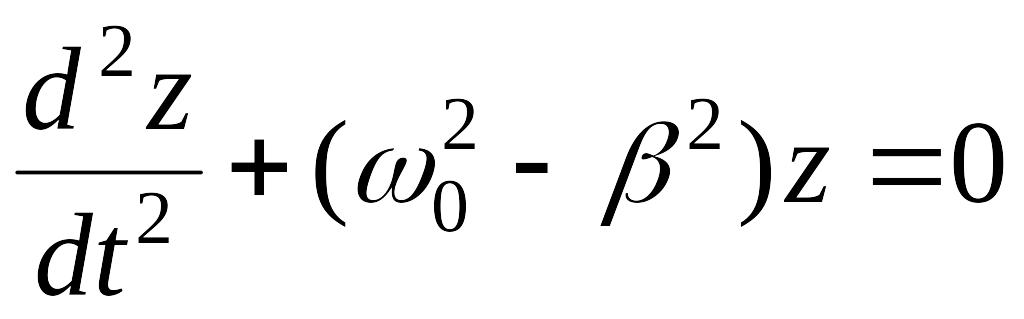. (3.7)

Это уже близко к (2.3). Решение уравнения (3.7) существенно зависит от знака выражения в скобках .

Пусть трение достаточно мало, так чтобы выполнялось условие:

. (3.8)

Обозначим:

. (3.9)

Уменьшение частоты при трении следовало ожидать заранее, так как трение вообще задерживает движение. Имеем:

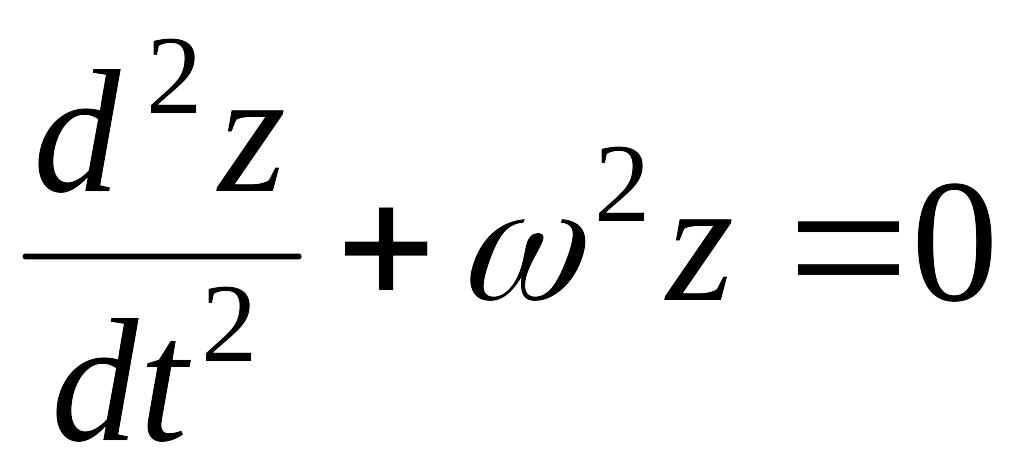. (3.10)

Уравнение (3.10) совпадает с (2.3). Его решение – (2.7):

, (3.11)

где – амплитуда колебаний в начальный момент времени. Величина колеблется гармонически с периодом , где частота колебаний определяется из (3. 9), так что

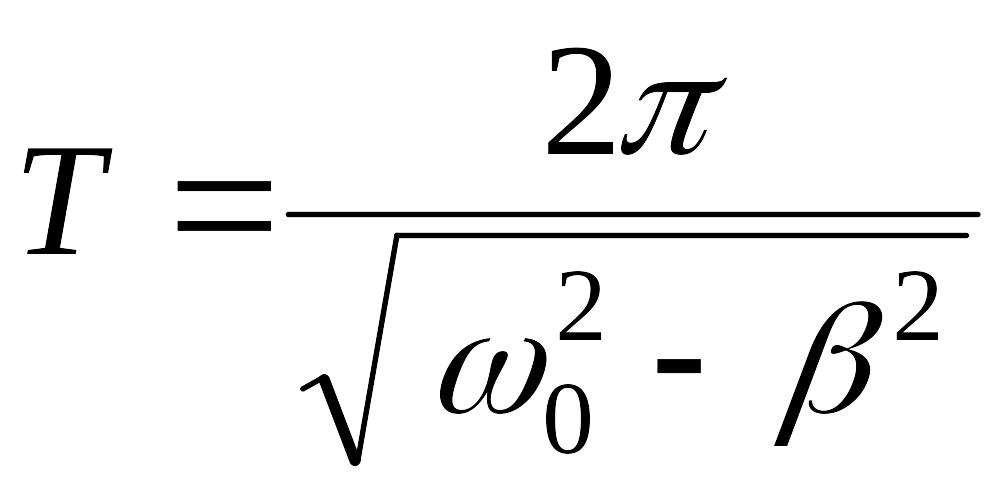. (3.12)

Вернемся к прежней переменной и подставим (3.11) в (3.6):

. (3.13) Эта функция является произведением убывающей показательной функции и синусоидальной функции . Описываемое ею движение представляет собой затухающие колебания (рис. 3.1а) Это движение можно рассматривать, как гармонические колебания с экспоненциально убывающей амплитудой , уменьшающейся от периода к периоду (рис. 3.1б).

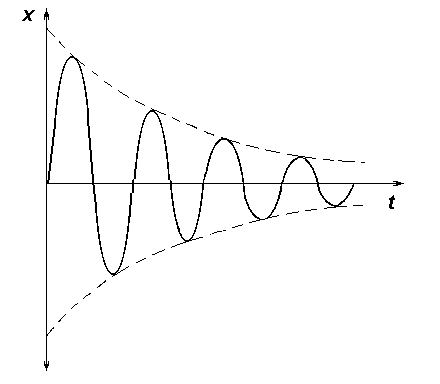
Рис. 3.1а. График затухающих колебаний

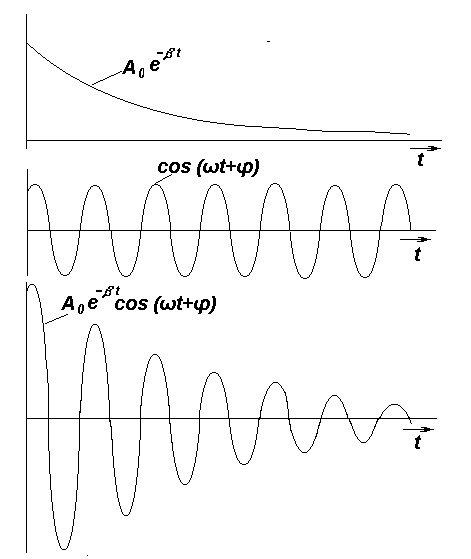
Рис. 3.1б. График затухающих колебаний

Строго говоря, (3.13) – уже отнюдь не гармоническое колебание; не является периодической функцией. Однако расстояние во времени между двумя последовательными прохождениями системы через положение равновесия (в одном и том же направлении) постоянно и равно (3.12). Точно так же постоянно и равно той же самой величине расстояние во времени между двумя последовательными максимальными отклонениями. Этот промежуток времени мы будем называть условным периодом затухающего осцилляторного процесса.

3.2.2. Логарифмический декремент затухания. Натуральный логарифм отношения значений двух последовательных амплитуд колебаний называется логарифмическим декрементом затухания :

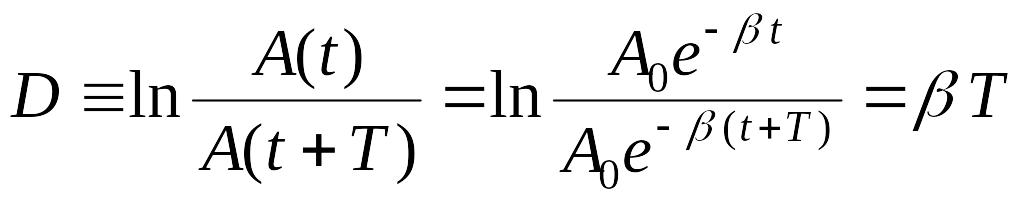. (3.14)

Логарифмический декремент характеризует затухание колебаний за период, в то время как коэффициент затухания характеризует затухание колебаний за единицу времени. Каков физический смысл : обозначим через число колебаний, по прошествии которых амплитуда уменьшается в раз, а  промежуток времени, соответствующий этому уменьшению. Тогда: и

С другой стороны , но, по определению и

. (3.15)

– есть величина, обратная числу колебаний, по истечении которых амплитуда спадает в раз. Пусть . Это значит, что амплитуда колебаний уменьшается в раз по истечении 100 колебаний.

3.2.3. Добротность. Для характеристики колебательных систем часто (особенно в радиотехнике) употребляется еще величина, называемая добротностью и обычно обозначаемая буквой . Она определяется как:

. (3.16)

Добротность системы есть умноженное на число полных колебаний, по истечении которых амплитуда уменьшается в раз.

3.2.5. Затухающие колебания в электрическом колебательном контуре. Примем во внимание сопротивление катушки.

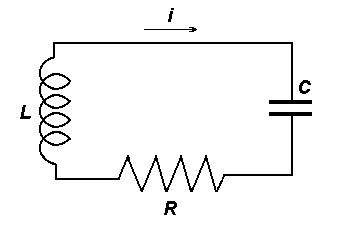
Рис. 3.2. Электрический колебательный контур с затуханием

Согласно второму правилу Кирхгофа сумма падений напряжения в контуре равна сумме действующих в нем ЭДС:

.

Слева стоит сумма разностей потенциалов на конденсаторе и на сопротивлении, справа – ЭДС самоиндукции. Учитывая, что , получим дифференциальное уравнение:

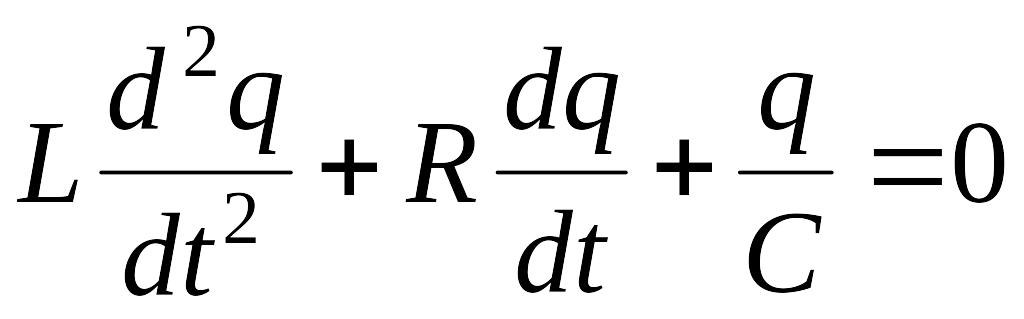. (3.17)

Разделим обе части этого уравнения на и введем обозначения:

, (3.18)

. (3.19)

Тогда окончательно:

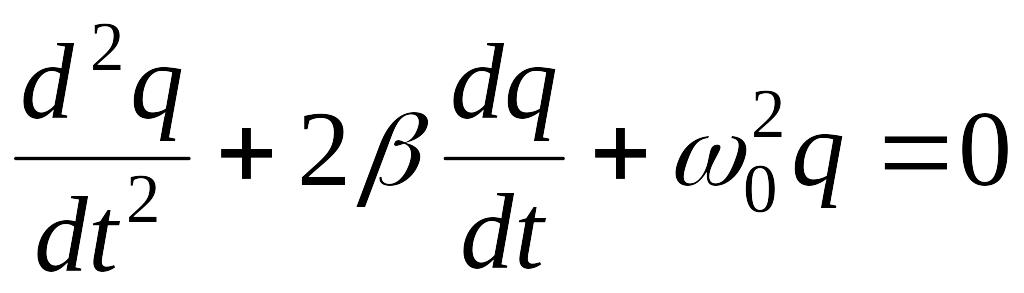. (3.20)

Уравнение (3.20) полностью аналогично (3.5). Его решение, так же как и решение (3.5), имеет различный характер в зависимости от соотношения между коэффициентами. Предположим, что частота собственных электрических колебаний велика, т. е. . Тогда, полагая, как и в случае механических колебаний , мы можем записать решение (3.20) в виде, аналогичном (3.13):

. (3.21)

Частота электрических колебаний зависит от коэффициента затухания :

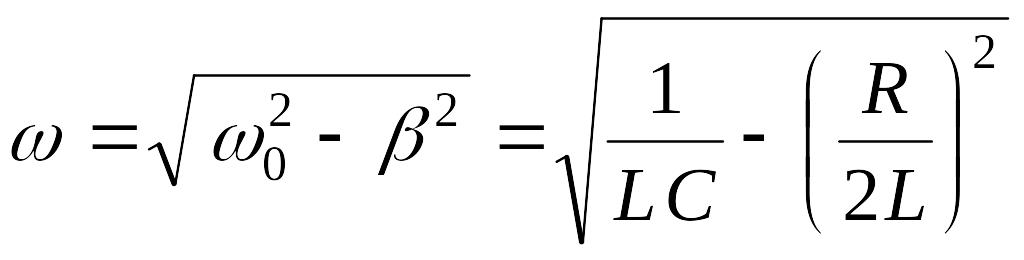. (3.22)

С увеличением сопротивления контура частота уменьшается, а период колебаний 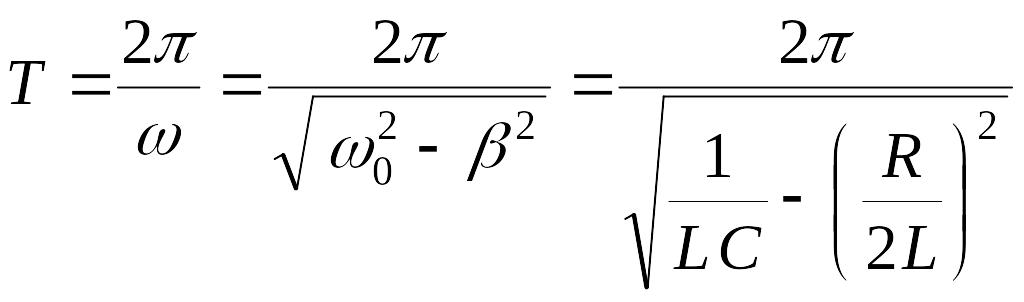увеличивается.

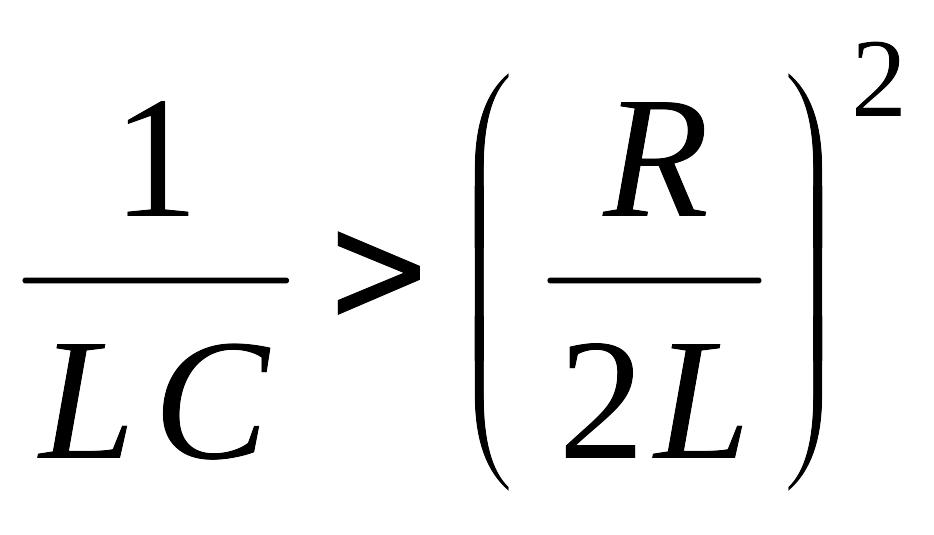Формулы (3.21) и (3.22) имеет непосредственный физический смысл только в том случае, если – действительная величина, т. е. если выполнено условие или , или ,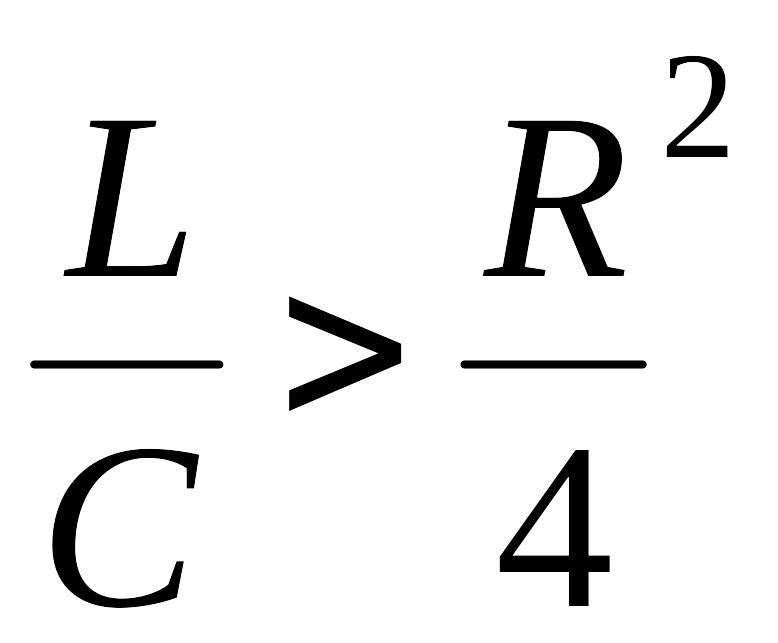

или еще 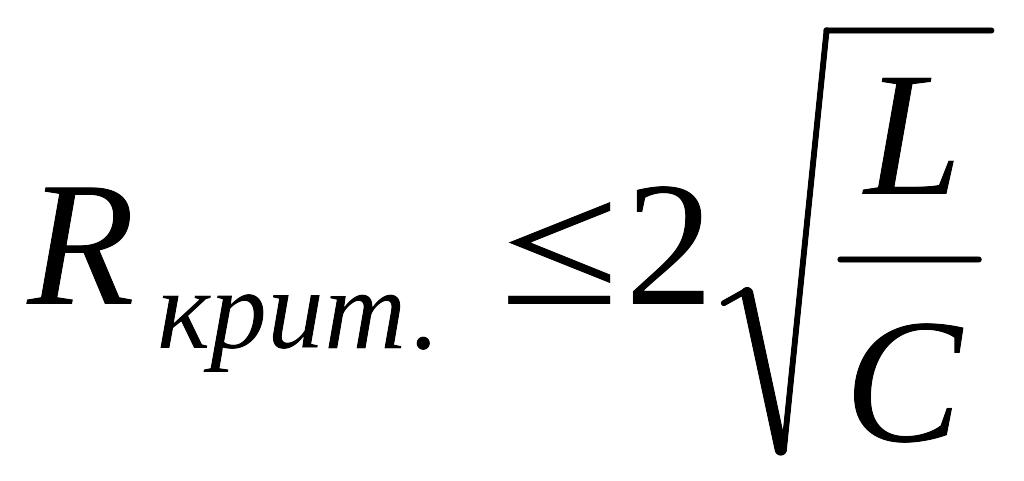. (3.8б)

Для возможности электрических колебаний необходимо, чтобы сопротивление контура было меньше критического сопротивления . При условии мы имеем апериодический разряд.