36

1. Кинематика гармонических колебаний

1.2. Основные понятия и определения

1.2.1. Колебательное движение. Общие условия возникновения и существования колебаний. Движение веток в ветреную погоду, маятника часов, смычка скрипача, крыльев птиц повторяется через определенные промежутки времени. Такие многократно повторяющиеся движения называют колебательными движениями, или, кратко, колебаниями.

Колебания свойственны всем явлениям природы: пульсирует излучение звёзд, внутри которых происходят циклические ядерные реакции; с высокой степенью периодичности вращаются планеты Солнечной системы; движение Луны вызывает приливы и отливы на Земле; ветры возбуждают колебания и волны на поверхностях водоёмов. Внутри любого живого организма  от одиночной клетки до высокоорганизованных их популяций  непрерывно происходят разнообразные, ритмично повторяющиеся процессы: биение сердца, колебания психических состояний и др. В виде сложнейшей совокупности колебаний частиц и полей (электронов, фотонов, протонов и др.) можно представить «устройство» микромира.

В физике особо выделяются колебания двух видов  механические и электромагнитные. Это обусловлено той исключительной ролью, которую играют гравитационные и электромагнитные взаимодействия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большую часть прямой информации об окружающем мире.

Колебания любых физических величин почти всегда сопровождаются попеременным превращением энергии одного вида в энергию другого вида. Так, оттягивая маятник от положения равновесия, мы увеличиваем потенциальную энергию груза, запасённую в поле тяжести; при отпускании он начинает падать, вращаясь около точки подвеса как около центра, и в крайнем нижнем положении вся потенциальная энергия превращается в кинетическую. Поэтому груз проскакивает это равновесное положение, и процесс перекачки энергии повторяется, пока рассеяние энергии, обусловленное, например, трением, не приведёт к полному прекращению колебаний.

Для того чтобы совершалось колебательное движение необходимо 1) чтобы одним из возможных положений тела было положение его устойчивого равновесия; 2) после того как тело выведено из положения устойчивого равновесия, должна появиться сила, возвращающая его в исходное состояние.

1.2.2. Параметры колебательного движения. Самый характер движений определяет и те вопросы, которыми обычно интересуются при изучении колебаний. При изучении неповторяющихся движений мы чаще всего интересуемся положением, скоростью и ускорением движущихся тел в какой-то момент времени. В колебательном движении нас главным образом интересует уже не состояние системы в данный момент времени, а признаки, характеризующие повторяемость движения. Это  закон, по которому повторяется движение, время, через которое система снова приходит к тому же самому состоянию, наибольшие отклонения, которых достигает движущееся тело.

Для рассмотрения колебательного процесса удобен геометрический способ представления, который сводится к следующему (рис. 1.1).

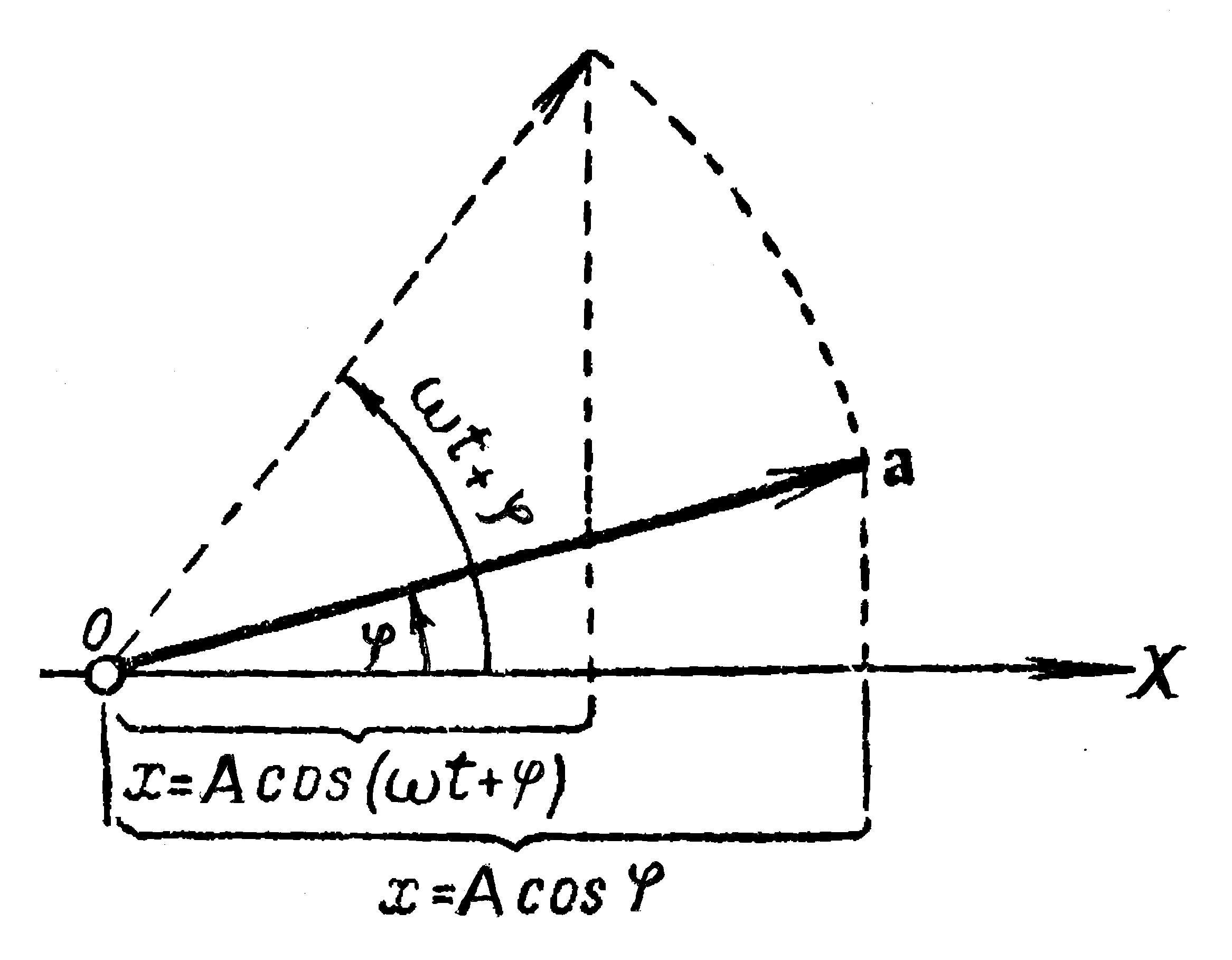
Рис. 1.1. Представление гармонического колебательного движения как движения проекции вектора , вращающегося с постоянной угловой скоростью

Возьмем ось, назовем ее осью и выберем на ней произвольную точку . Из этой точки под углом отложим вектор , величина которого . Спроецируем конец вектора на ось . Из рисунка видно, что координата точки, в которую спроецировался конец вектора , равна

. (1.1)

Будем равномерно вращать вектор с угловой скоростью против часовой стрелки. Тогда координата конца вектора будет изменяться в пределах от до . Для произвольного момента времени вектор образует с осью угол, равный , при этом координата конца вектора будет равна

. (1.2)

Мы видим, что координата конца вектора или, что то же самое, величина проекции вектора на некоторую ось будет совершать колебательное движение, т. к. время входит в (1.2) через периодическую функцию. Это значит, что существует такой интервал времени , что

. (1.3)

Промежуток времени, в течение которого совершается одно полное колебание, называется периодом колебаний . Обратная величина периода

(1.4)

называется линейной частотой. Линейная частота измеряется в герцах; 1 Гц – частота такого периодического процесса, период которого равен 1 с. Из (1.3) следует, что

. (1.5)

Величина называется круговой (циклической) частотой колебаний. Она измеряется в радианах в секунду . Сравнивая (1.4) и (1.5), получим связь между и

. (1.6)

Множитель в (1.2) определяет максимальное значение колеблющейся величины и называется амплитудой колебаний, аргумент косинуса - фазой, а постоянная - начальной (в момент времени фазой колебания. Можно сказать, что фазой колебания называют величину, определяющую в данный момент времени (совместно с амплитудой) значение колеблющейся величины и измеряемую промежутком времени (в долях периода), истекшим от начала колебательного процесса.

1.2.3. Гармонические колебания. Колебательное движение, при котором физическая величина изменяется с течением времени по закону синуса или косинуса, называется гармоническим колебательным движением или просто гармоническим колебанием. Ни в природе, ни в технике никогда не встречаются строго периодические гармонические колебания. Тем не менее, изучение гармонических колебаний очень важно по двум основным причинам: 1) в природе и в технических устройствах часто возникают колебания, мало отличающиеся на протяжении достаточно большого промежутка времени от гармонических; 2) существует очень широкий класс физических систем (т. н. спектральные приборы), которые преобразуют произвольные (негармонические) колебания в набор колебаний, близких к гармоническим, осуществляя гармонический анализ.

1.2.4. Скорость и ускорение при гармоническом колебательном движении. Если точка совершает гармонические колебания, то ее смещение равно:

. (1.7)

Скорость численно равна производной по времени от смещения:

. (1.8)

Ускорение точки можно получить, взяв производную от скорости по времени:

. (1.9)

Из формул (1.8) и (1.9) видно, что скорость и ускорение точки, совершающей гармонические колебания, также изменяются по гармоническому закону с той же частотой. При этом амплитуда скорости , а амплитуда ускорения . По фазе скорость сдвинута на , а ускорение – на относительно смещения.

Равенство (1.9) на основании (1.7) может быть переписано:

.

Мы видим, что ускорение при гармоническом колебании пропорционально смещению и направлено к положению равновесия. Уравнение

(1.10)

носит название дифференциального уравнения гармонических колебаний.