5. Косвенное измерение – измерение, при котором значение физической величины определяют на основании результатов прямых измерений других физических величин, функционально связанных с искомой.

Обработка косвенных измерений

В лабораторной практике большинство измерений – косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин:

N = ƒ (x, y, z, ...)  (13)

Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (13) средних значений непосредственно измеряемых величин, т.е.

¯N = ƒ (¯x, ¯y, ¯z, ...)  (14)

Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных.

Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам

   (15)  или

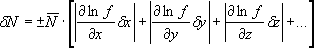,   (16)

где 

частные производные функции N = ƒ(x, y, z, ...) по аргументу x, y, z..., найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные; δx, δy, δz – систематические ошибки аргументов.

Формулой (15) удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (16) применять целесообразно, если функция имеет вид произведения или частного аргументов.

Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:

  (17)   или

, (18)

где Δx, Δy, Δz, ... – доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов x, y, z, ... . Следует иметь в виду, что доверительные интервалы Δx, Δy, Δz, ... должны быть взяты при одинаковой доверительной вероятности P₁ = P₂ = ... = P_n = P.

В этом случае надежность для доверительного интервала ΔN будет тоже P.

Формулой (17) удобно пользоваться в случае, если функция N = ƒ(x, y, z, ...) имеет вид суммы или разности аргументов. Формулой (18) удобно пользоваться в случае, если функция N = ƒ(x, y, z, ...) имеет вид произведения или частного аргументов.

Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:

.

При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений.

Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения ΔN = ε ¯N найти абсолютную погрешность.

Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий.

При обработке результатов косвенных измерений предлагается следующий порядок операций:

1. Все величины, находимые прямыми измерениями, обработайте в соответствии с правилами обработки результатов прямых измерений. При этом для всех измеряемых величин задайте одно и то же значение надежности P.

2. Оцените точность результата косвенных измерений по формулам (15) – (16), где производные вычислите при средних значениях величин. Если ошибка отдельных измерений входит в результат дифференцирования несколько раз, то надо сгруппировать все члены, содержащие одинаковый дифференциал, и выражения в скобках, стоящие перед дифференциалом взять по модулю; знак d заменить на Δ (или δ).

3. Если случайная и систематическая ошибки по величине близки друг к другу, то сложите их по правилу сложения ошибок. Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.

4. Результат измерения запишите в виде:

N = ƒ (¯x, ¯y, ¯z, ...) ± Δƒ.

5. Определите относительную погрешность результата серии косвенных измерений

_{ε =}   Δƒ  _{· 100%.} ¯¯ƒ¯

5. сбор априорной информации при планировании эксперимента

Началом экспериментального исследования является сбор, изучение и анализ всех имеющихся данных об объекте. Априорная информация может быть скупой или обширной, но именно она является той базой, на которой строятся первые шаги исследования. В результате проведения предварительного этапа (априорного) исследователь должен:

1. Составить полный список факторов, исходя из того, что лучше назвать несколько малозначащих факторов, чем пропустить один существенно значимый.

2. Задать ориентировочные приделы изменения факторов с учётом требований их совместимости (процесс может быть реализован при этих сочетаниях пределов).

3. Выбрать параметры оптимизации в соответствии с поставленной задачей.

Если список факторов большой (более 7) необходимо выполнить отсеивание малозначащих факторов. На этом завершается предварительная подготовка к эксперименту.

В соответствии с идеей шагового поиска эксперимент проводится в несколько этапов. Число этапов и действия на каждом из них зависят от результатов предыдущего этапа и конечной цели исследования.

Всё многообразие конечных целей исследования можно обобщённо разделить на 2 типа:

1. Найти адекватное описание функций отклика в заданной части факторного пространства.

2. Найти оптимальные условия протекания процесса.

6. Статистические характеристики выборки

Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.

При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборка подразделяется на повторную и бесповторную.

Повторной называют выборку, при которой отобранный объект возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть представительной.

Выборка будет представительной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.

Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть, то различия между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает.

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, x₂-n₂ раз, х_k-n_k раз и Σni=n-объем выборки. Наблюдаемые значения xi называют вариантами, а последовательность вариант, записанных в общем в возрастающем порядке,- вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборку - относительными частотами.

Размах варьирования:

R=X_max-X_min

Среднее значение:

СКО -

Коэффициент вариации (показывает относительное колебание отдельных значений около средней арифметической):

: