Введение

Важнейшей характеристикой современного строительства являются качество изготовления конструкций, их установка и монтаж. Большую роль играет соблюдение проектных размеров как всего сооружения в целом, так и отдельных его элементов. Но размеры конструкций и сооружения после их изготовления и монтажа могут в значительной степени отличаться от проектных. Отклонение действительных параметров может быть как положительным (в сторону увеличения), так и отрицательным (в сторону уменьшения). Отсюда следует, что все размеры имеют свои предельные значения: наибольший xmax и наименьший xmin (рис.1). На рис.1. рассматривается в качестве объекта рельсовый путь мостового полярного крана. Разность между экстремальными значениями составляют допустимую величину положения объекта δ, т.е.

δ= xmax- xmin (1)

Необходимо подразделить все размеры и допуски на конструкционные и производственные. К конструкционным относятся те, которые удовлетворяют оптимальным эксплуатационным требованиям, предъявляемым к сооружениям. К производственным допускам относятся такие, которые необходимо соблюдать в процессе изготовления конструкций, при выполнении строительно-монтажных работ. Необходимо, чтобы эти допуски соответствовали всем требованиям, предъявляемым проектом к качеству сооружения. Все допуски устанавливаются исходя из расчета точности конструкций. Установленная проектом точность определяется допуском, а полученная точность оценивается ошибками, возникшими при производстве строительно-монтажных работ, и в процессе производства геодезических измерений.

Границы максимальных отклонений

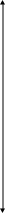
X

Номинальный параметр сооружения

Рис.1.

Применение геодезических методов ставит ряд задач, которые необходимо решать на различных этапах. На предварительном этапе, включающем в себя предварительную оценку состояния объекта, и всех последующих, заключающихся в проведении работ по определению полной геометрии сооружения с учетом его напряжно-деформационных нагрузок, необходимо установить достаточную точность геодезических измерений. В дальнейшем появляются вопросы, связанные с устранением отклонений параметров объекта от номинальных. В таких случаях требуется особый подход к оценке как самого состояния сооружения, так и к точности геодезических работ, при этом их можно увязать друг с другом, т.е. техническое состояние влияет на производство геодезических работ и точность геодезических измерений, что позволяет оценить состояние объекта.

1. Основные положения по анализу точности.

Точность и допуски необходимо рассматривать как качественную оценку, характеризующую конструкции, сооружения в целом, подготовительные работы, строительство и монтаж. При этом система допусков представляет собой стандартизацию точности технологических процессов при возведении сооружения, опирающуюся на предельные ошибки. Исходя из вероятностного подхода к теории ошибок измерений было установлено, что случайные ошибки результатов измерений подчиняются нормальному закону распределения. Знание функции плотности распределения таких ошибок дает возможность для решения целого ряда задач, возникающих в ходе геодезических работ:

1)определение наиболее вероятного значения измеряемой величины;

2)установление предельных значений (допусков) для конкретно вида работ;

3)вычисление вероятности появления случайной ошибки в

определенном интервале;

4)выявление предельных значений, после которых ошибки можно квалифицировать как грубые.

Для этого воспользуемся функцией Лапласа, имеющей следующий вид: 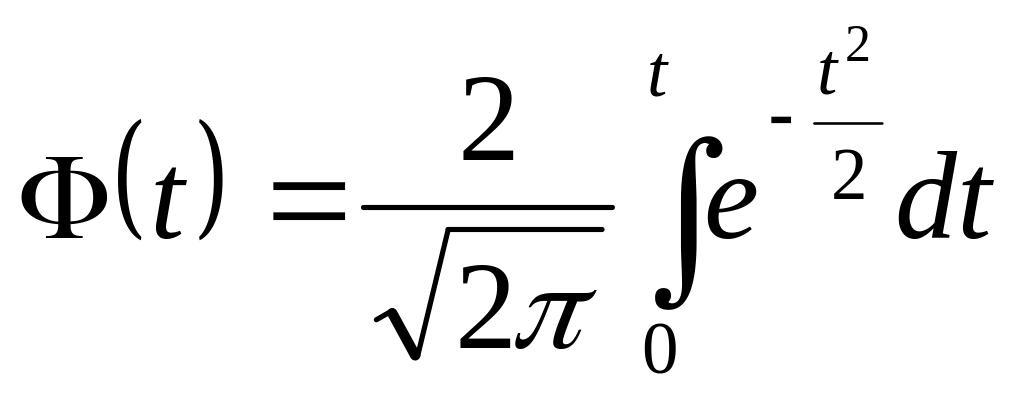(2)

Где t- нормированный параметр функции Лапласа.

Вероятность того, что случайная величина х примет значение, принадлежащее интервалу (α;β), можно выразить через функцию распределения:

Р(α<x<β)=F(β)-F(α). (3)

Переходя к нормированной случайной величине t, имеем:

Р( tα < t < t β ) = Ф(tβ )-Ф( t α) (4)

где tα = ; t β= ;

а-математическое ожидание случайной величины;

σ-среднее квадратическое отклонение случайной величины.

Определим вероятность того, что нормально распределенная величина х отклоняется от своего математического ожидания на величину, меньшую чем ε , т.е. найдем вероятность осуществления неравенства:

a - ε < x < a+ ε.

Так как t=ε/σ, то:

Р( tα < t < t β )=Ф . (5)

Окончательно имеем:

Р(/ х – а / < ε )=Ф . (6)

Или

Р(/ х – а / < tσ )=Ф(t). (7)

Таким образом, значение Ф(t) при заданном t определяет вероятность того, что отклонение нормально распределенной величины по абсолютному значению меньше tσ. Доверительная вероятность:

Р( / х – а / < σ )=Ф(1)=0,6827 при t= 1;

Р( / х – а / < 2σ )=Ф(2)=0,9545 при t= 2;

Р( / х – а / < 3σ )=Ф(3)=0,9973 при t= 3.

Из последнего равенства следует, что практически рассеивание случайной величины укладыватся на участке М ± 3σ. Можно считать, что предельным значением ошибки является величина 3σ , а в качестве допуска – ее удвоенное значение, т.е. δ= 6 σ .

2. Методика расчета оптимальных параметров сооружения

Рассмотрим данный вопрос на примере определения расстояния рельсового пути мостового полярного крана, проектная ось которого показана на рис.1. По результатам геодезической съемки определялось фактическое положение оси, при этом для определения координат Xi,, Yi, Zi использовался электронный тахеометр SET 6F. Местом стояния тахеометра является маркированная точка (СТ) с координатами:

Хст= 100.0000 м.

Yст= 100,0000 м.

Наблюдения точек в других поясах выполняются лазерной рулеткой и оптическим теодолитом 3Т5КП. Результатами измерений являются расстояния, вертикальные и горизонтальные углы, по значениям которых вычисляются координаты исследуемых точек. При этом станции стояния прибора выбираются на раме полярного крана в зависимости от условий видимости и их координаты будут определены методом обратной угловой засечки. В качестве исходных принимаются точки подкранового пути с известными координатами.

Для обработки результатов измерений применяют метод, заключающийся в том, что по координатам точек в каждом поясе вычисляются длины хорд:

. (8)

По величинам l определяют радиусы описанной окружности треугольника, заданного координатами вершин 1(Xi’-1,Yi-1), 2(Xi’,Yi), 3(Xi+1,Yi+1) (рис.2.):

Ri= (9)

При этом число радиусов Ri , полученных путем вычисления по образованным вариантам треугольников, будет соответствовать числу этих треугольников к , вершинами которых являются исследуемые точки поясов. Значение к вычисляется по формуле:

k=(n/3)-(n /2)+(n /6), (10)

где n – число точек, образующих пояс (рис.2).

Для анализа технического состояния сооружения необходимо использовать все возможные варианты определения радиусов при решении треугольников. На рис.3 показано висло треугольников для 11 определяемых точек окружности, по которым вычислялись радиусы.

Оптимальный радиус Rопт окружности пояса будет равен арифметической средине из совокупности вычисленных значений:

Rопт = (11)

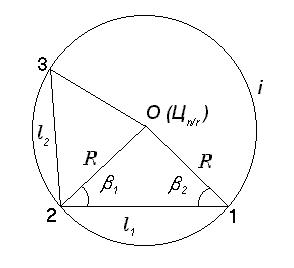
Рис.2 Схема элементов оптимальной окружности.

Величина оптимального радиуса Rопт является характерным геометрическим параметром исследуемого сечения.

Координаты центра оптимальной окружности определяют следующим образом. В треугольниках находят углы β1 и β2 (рис.2).

β1= β2= β=arccos (12)

Координаты центра (X0;Y0) будут получены по формулам полярной засечки. Для этого вычисляют дирекционные углы направлений радиусов:

α0-i=αi-(i+1)+180-β, (13) , где

αi-(i+1) =arctg , (14)

Вычисленные координаты (Х0(i);Y0(i)) определяется по известным формулам:

Х0(i)=Xi+Rопт cosα0-i; (15)

Y0(i)=Yi+Rопт sinα0-i.

Вероятнейшие значения координат центра (Х0;Y0) будут определены согласно нижеследующих выражений:

Х0=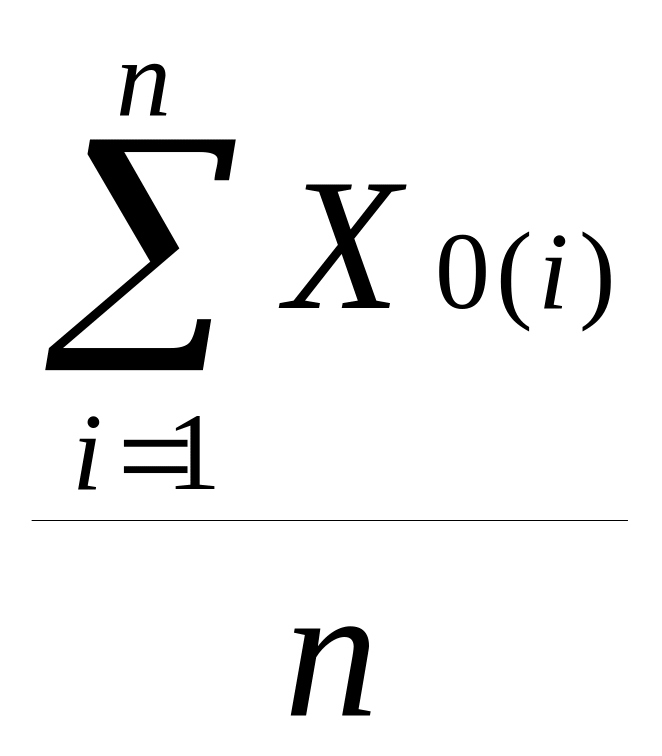 , (16)

Y0= .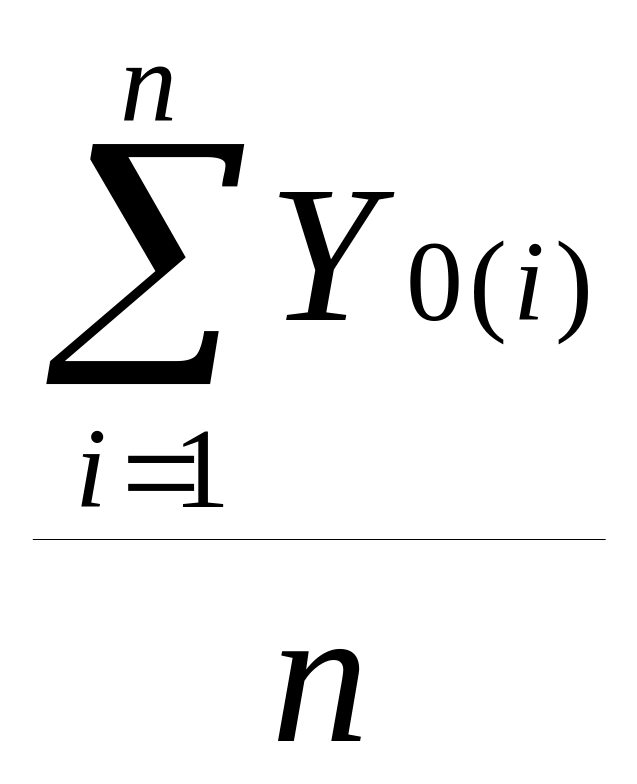

Используя координаты текущих точек (Хi;Yi) и координаты центра оптимальной окружности, находим фактические радиусы:

RФ= . (17)

Затем вычисляем уклонения фактического радиуса RФ от оптимального Rопт в горизонтальной плоскости:

νx=RФ-Rопт., (18)

где νx – отклонения пути от номинального (оптимального) положения по оси Х;

νy=(RФ) . (19)

где Xij,Yij – координаты исследуемых точек в смежных циклах наблюдений;

νy – отклонения пути от номинального положения по оси Y .

3. Вычисление эмпирических характеристик распределения.

Практически при многократных измерениях полученные результаты х1,х2,…,хn группируют по классам (интервалам), определяя частоту n1,n2,…,nk появления этих результатов в соответствующем классе и вычисляя эмпирические (приближенные) значения вероятностей – частости:

(20)

где j=1,2,…,k и

(21)

Применение систем классов необходимо при обработке больших рядов распределения случайной величины. Для определения шага интервала используют формулу Г. Стерджесса:

(22)

где xmax , xmin - соответственно максимальное и минимальное значения случайной величины;

n – число наблюдени.

Вычисляют накопленные частоты согласно

Nj=n1+n2+…+nj. (23)

Затем определяют накопленную частость или эмпирическую функцию распределения Fn(x)

Fn(x)= (24)

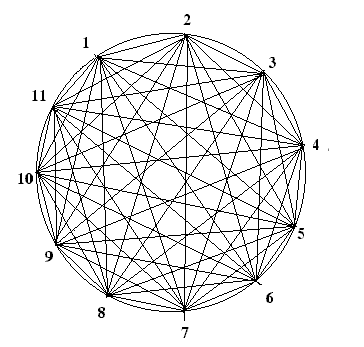
Рис. 3

Для решения поставленной задачи необходимо подвергнуть данный ряд распределения статистическому анализу. При этом определяют эмпирические числовые характеристики распределения: математическое ожидание, дисперсию, среднее квадратическое отклонение, асимметрию и эксцесс. В дальнейшем проводится оценка точности параметров распределения. Для выявления случайного характера распределения значений горизонтального угла проверяется гипотеза близости данного ряда нормальному закону распределения.

Для проведения группирования сначала нужно установить шаг интервала:

м