1.12. Геометричні характеристики плоских перерізів

До основних геометричних характеристик плоских перерізів відносяться площа поперечного перерізу, статичні моменти площі, моменти інерції, радіуси інерції, моменти опору. Ці величини використовують при розрахунках на міцність, жорсткість і стійкість конструкцій.

1.12.1. Площа поперечного перерізу.

Розглянемо плоский переріз довільної форми (рис.1.12.1). Виділимо на цьому перерізі елементарну площадку dS. Тоді площа перерізу буде дорівнювати:

, [ м²].

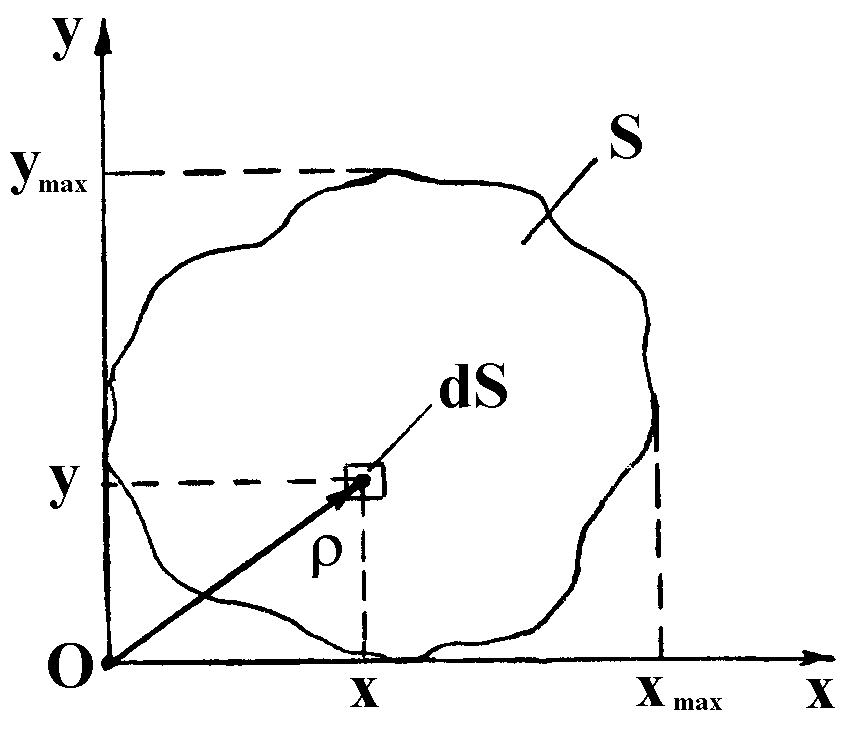
Рис.1.12.1. Схема для визначення геометричних характеристик плоского перерізу.

1.12.2. Статичні моменти площі.

Статичні моменти площі визначають за формулами:

, , [ м³] .

Якщо відомі координати центра тяжіння фігури, то статичні моменти визначаються так:

S_x = y_c· S , S_y = x_c· S ,

де x_c , y_c – координати центра тяжіння фігури.

1.12.3. Моменти інерції площі поперечного перерізу.

Розрізняють осьові моменти інерції, а також полярний та відцентровий моменти інерції:

a) осьові моменти інерції:

, [ м⁴] ;

, [ м⁴] .

б) полярний момент інерції:

, I_p = I_x + I_y , [ м⁴];

в) відцентровий момент інерції:

; [ м⁴] .

Дві взаємноперпендикулярні осі, щодо яких відцентровий момент інерції дорівнює нулю, називаються головними.

Дві взаємоперпендикулярні осі, одна з яких є віссю симетрії фігури, завжди є головними.

Якщо головні осі проходять через центр тяжіння фігури, то вони називаються головними і центральними.

1.12.4. Осьові моменти опору.

Осьовим моментом опору називають відношення моменту інерції відносно даної осі до відстані до найбільш віддаленої точки перерізу:

W_x= І_х /у_max , W_y = І_у /х_{max ,} [м³].

1.12.5. Геометричні характеристики простих фігур.

Допустимо балка має прямокутний переріз (рис.1.12.2.).

Т оді осьовий момент інерції буде дорівнювати:

І_х = = ²dy = 2b ²dy =

= │ = 2b · (h/2)³ / 3 = bh³ / 12 .

Аналогично:

І_y = hb³ / 12 .

Осьовий момент опору для прямокутного перерізу:

.

Рис.12.2.Розрахункова схема.

Осьовий момент опору для прямокутного перерізу:

.

Аналогічно:

.

Провівши аналогічні розрахунки для круглого поперечного перерізу отримаємо:

- осові моменти інерції:

І_x = І_y = d ⁴ / 64 , де d – діаметр круглого перерізу;.

- полярний момент інерції:

І_p = І_x + І_y = d ⁴ /32;

- осьові моменти опору:

W_x = W_y = І_x/(d/2) = d ³ /32;

- полярний момент опору:

W_P = І_p/(d/2) = d ³ /16 .

Моменти опору прокатних профілів (кутників, швелерів, двутаврів) наводяться в спеціальних довідкових таблицях.

1.13. Види навантажень та види деформацій

Прикладені до тіла зовнішні сили викликають різні внутрішні зусилля в поперечних перерізах цього тіла. В результаті тіло деформується. Існує п’ять видів навантажень (а також п’ять видів деформацій з такими ж назвами):

1. Розтяг - в поперечних перерізах тіла діє тільки подовжня сила N, що спрямована від перерізу. Стиск - сила N спрямована до перерізу.

2. Зсув (зріз) - в поперечних перерізах тіла діє тільки поперечна сила Q_x або Q_y.

3. Кручення - в поперечних перерізах тіла діє тільки крутний момент Т.

4. Згин - в поперечних перерізах тіла діє тільки згинаючий момент M_x або M_y.

5. Складна деформація - в поперечних перерізах тіла діє декілька зусиль (наприклад згинаючий і крутний моменти).