Найбільші дотичні напруження виникають в точках зовнішнього контура поперечного перерізу і обчислюються за формулою:

_max= T/ W_p ,

де W_p – полярний момент опору поперечного перерізу, м³ .

Для круглого поперечного перерізу: W_p = 2I_p / d = d³ / 16 ≈ 0,2 d³.

1.15.3. Епюри поперечних сил та згинаючих моментів при плоскому

поперечному згинанні.

Прямий брус, що підлягає плоскому вигину, називається балкою. При плоскому вигині в будь-якому перерізі балки усі внутрішні силові фактори дорівнюють нулю, крім згинаючого моменту і поперечної сили.

M ≠ 0; Q_y ≠ 0.

При побудові епюр поперечних сил та згинаючих моментів діють такі правила:

• поперечна сила Q_y в будь-якому перерізі балки чисельно дорівнює алгебраїчній сумі проекцій на вісь, перпендикулярну до осі балки, усіх зовнішніх сил, розташованих по одну сторону перерізу:

Q_y = ,

де n – кількість сил, що діють по одну сторону від перерізу;

P_i – проекція і-тої сили на вісь, перпендикулярну до осі балки;

- поперечна сила додатня, якщо вона обертає відсічену частину балки за годинниковою стрілкою, і від’ємна – якщо проти годинникової стрілки (рис.17.1.а);

- згинаючий момент M в будь-якому перетині балки чисельно дорівнює алгебраїчній сумі всіх зовнішніх згинаючих зосереджених моментів та згинаючих моментів від зовнішніх сил m_i, що прикладені по одну сторону перерізу:

М = ,

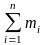де n – кількість зовнішніх зосереджених згинаючих моментів та згинаючих моментів від зовнішніх сил, що прикладені по одну сторону від перерізу;

m_i – і-тий зовнішній згинаючий момент;

• згинаючий момент від зовнішніх зусиль m_i вважають додатнім, якщо він вигинає відсічену частину балки відносно перерізу опуклістю вниз, і від’ємним – якщо опуклістю вверх (рис.1.15.1.б).

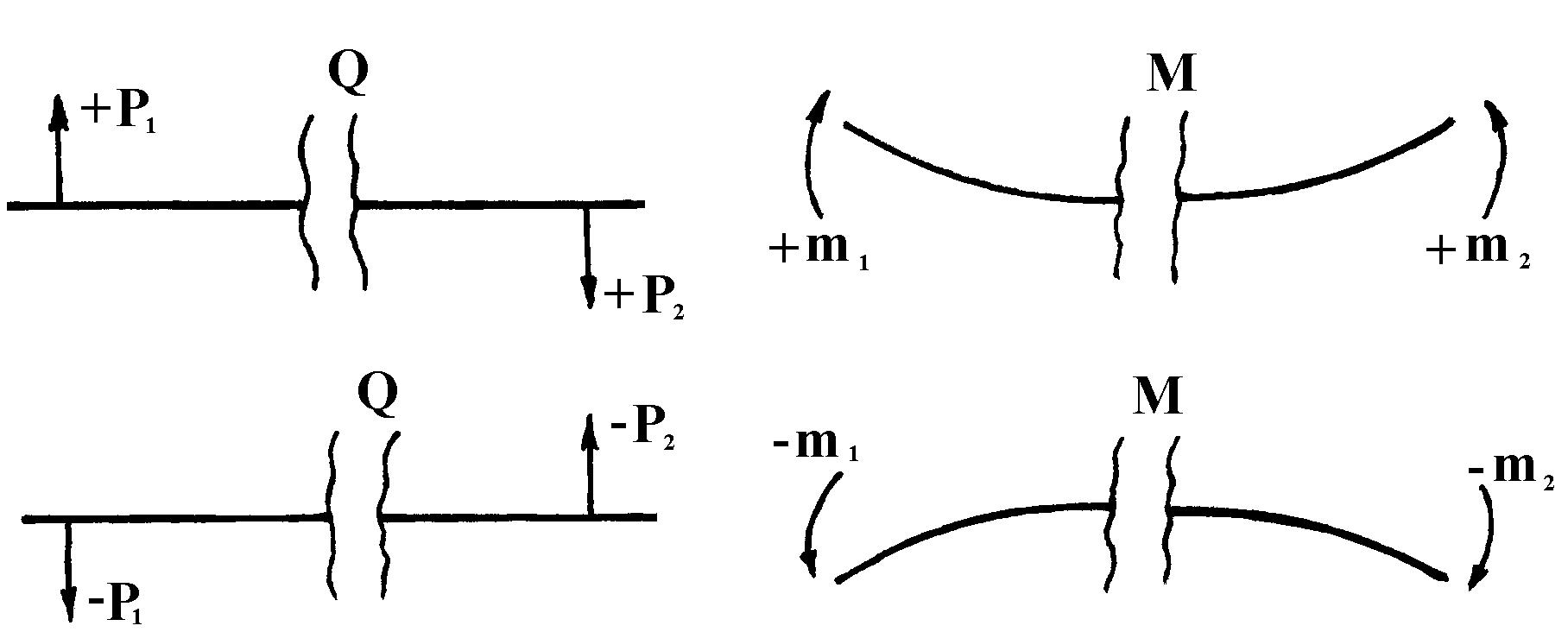
а б

Рис.15.1. Правило знаків при побудові епюр.

Використовуючи метод перерізів та розглянувши рівновагу відсіченої частини балки (лівої або правої) можна скласти рівняння залежності поперечних сил та згинаючих моментів від зовнішнього навантаження и абсцис перерізів. Отримані рівняння дозволяють побудувати епюри поперечних сил та згинаючих моментів.

16. Диференціальні та інтегральні залежності при

поперечному згинанні

Розглянемо двохопорну балку з довільним навантаженням (рис.1.16.1.).

На ділянці, де діє розподілене навантаження, виділимо нескінченно малий елемент довжиною dz. Цей елемент під дією поперечних сил Q і Q + dQ і згинальних моментів M і M + dM знаходиться в рівновазі.

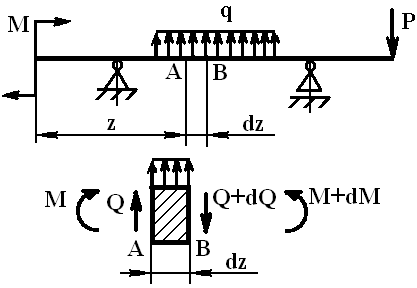
Рис.1.16.1. Схема навантаження двоопорної балки.

Складемо рівняння рівноваги:

- сума проекцій всіх сил на вертикальну вісь:

Y = 0 ; Q + q · dz - (Q + dQ) = 0;

звідси: q = dQ / dz ; (1.16.1)

- сума моментів відносно точки В :

M_B = 0 ; M + Q · dz - (M + dM ) + q · dz · dz / 2 = 0;

звідси: Q = dM / dz; (1.16.2)

Підставивши 1.16.2 в 1.16.1 отримуємо:

Q = d²M / dz² (1.16.3.)

Таким чином, похідна від згинаючого моменту по напрямку осі поперечного переріза дорівнює поперечній силі, а перша похідна від поперечної сили (друга похідна від згинаючого моменту) дорівнює інтенсивності розподіленого навантаження.

З формул (1.16.1) і (1.16.2) випливають наступні інтегральні залежності:

M =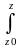 Q · dz ; (1.16.4)

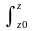Q = q · dz ; (1.16.5)

де z₀ - координата початку ділянки, z - координата довільного перерізу, що розглядається. Отже, знаючи закон зміни згинаючого моменту на ділянці, можна знайти закон зміни поперечної сили на цій ділянці і навпаки.