7.1.1 Алгоритм ручного рахунку

1. Обчислити коефіцієнт температуропроводності .

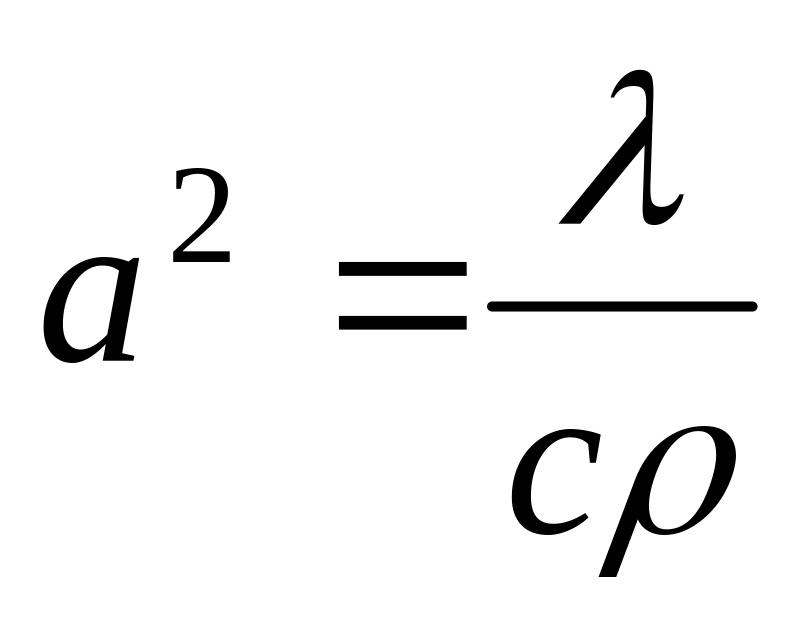2. Вибрати число 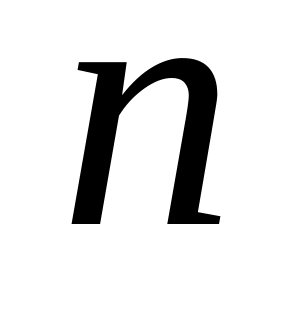поділу відрізка .

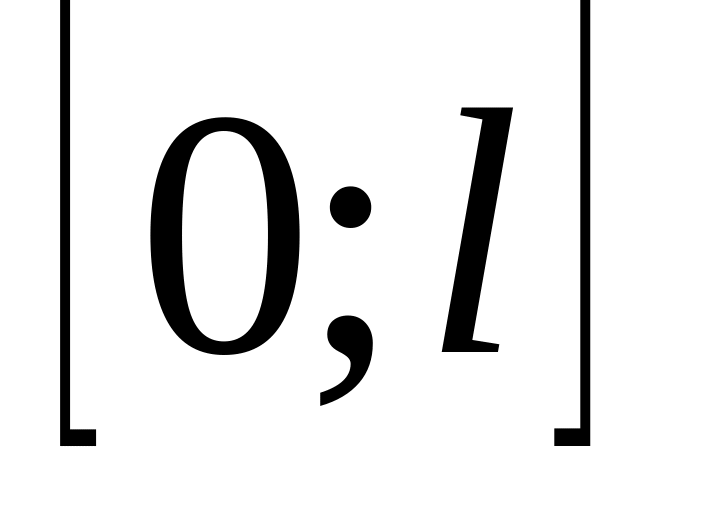3. Обчислити розбиття відрізка .

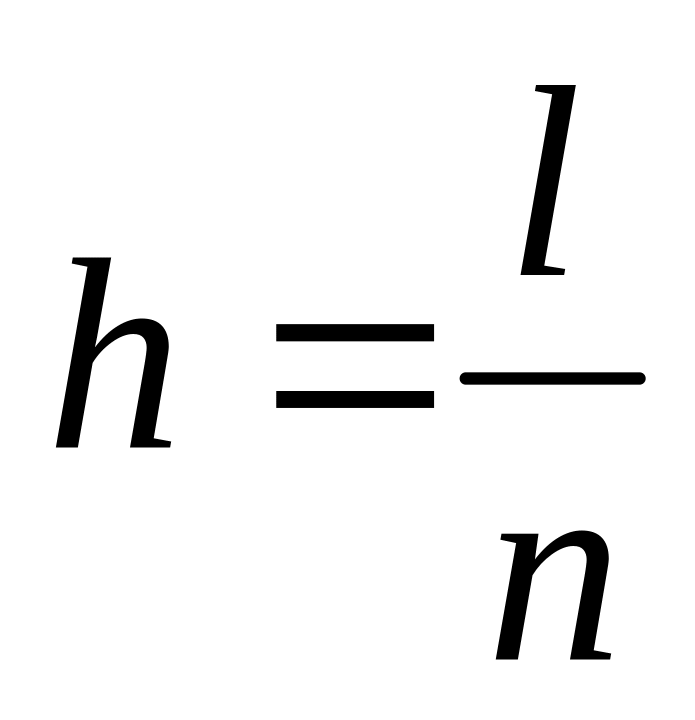4. Користуючись умовою стійкості (14) обчислити крок по 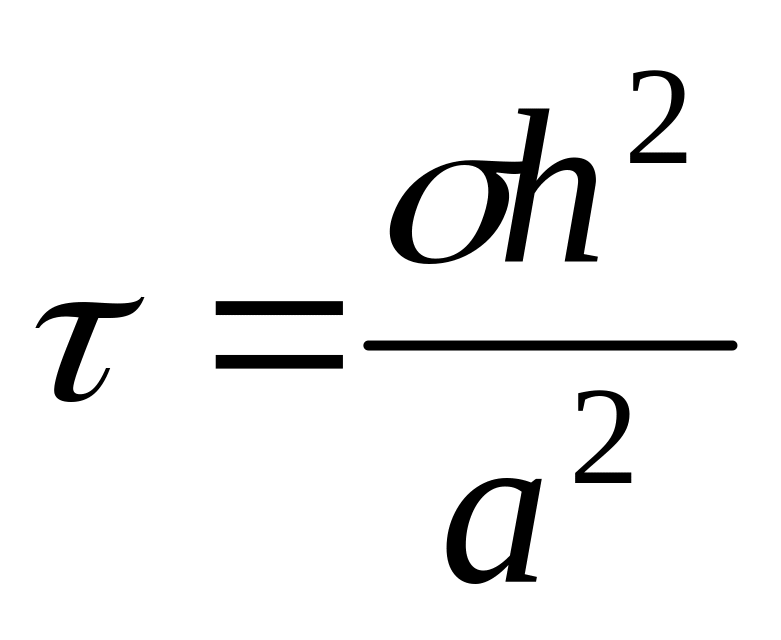поклавши .

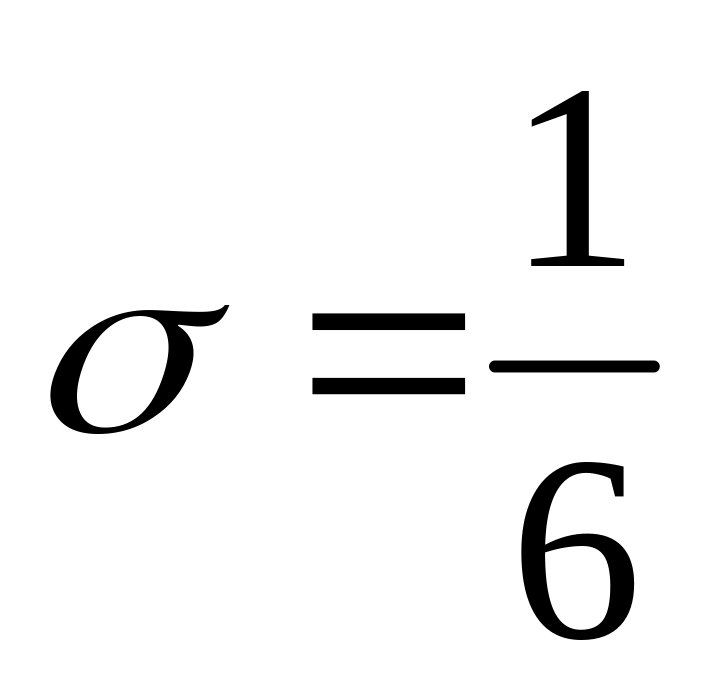5. При заданому 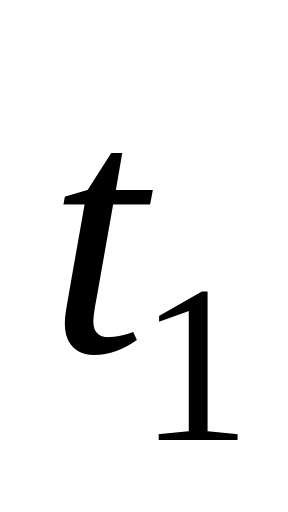обчислити кількість кроків по часу .

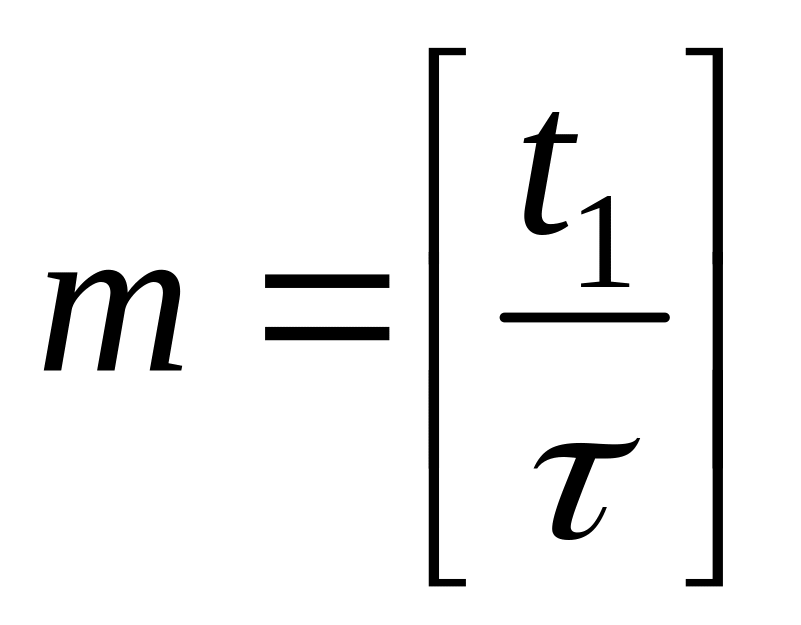6. Покрити область 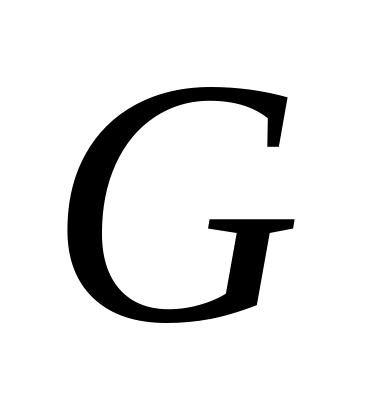прямокутною сіткою з кроками h і .

7. Користуючись початковою умовою обчислити 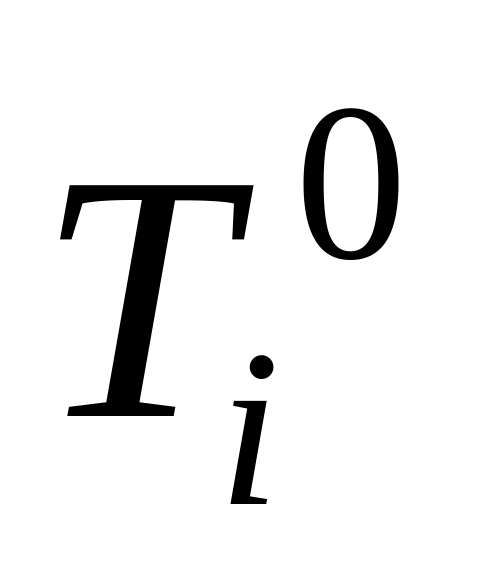(обчислити температуру на нижній основі прямокутної області).

8. Використовуючи граничні умови обчислити 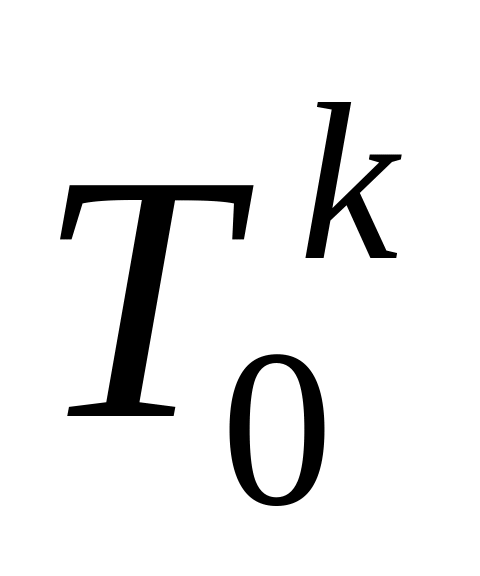, 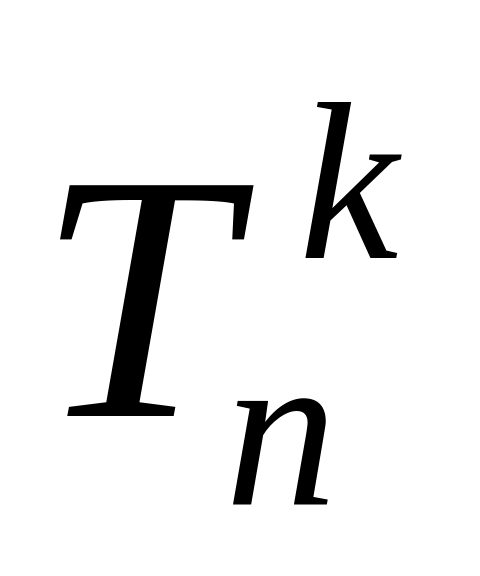де - температура на лівій межі, а - температура на правій межі.

9. Використовуючи MS Excel обчислити по явній різницевій схемі по функції (15) чи (16).

10. Обчислити розподіл температури у вузлах сітки.

Результати числових розрахунків занести в таблицю. Побудувати сімейство графіків.

7.2 Неявна різницева схема

Розглянемо неявну різницеву схему для І-ї крайової задачі для рівняння теплопровідності.

Як вже зазначалося, явна різницева схема досить проста для розуміння, але володіє істотними недоліками по відношенню до стійкості і при чисельних розрахунках прикладних задач в даний час майже не використовується спеціалістами.

По відношенню до стійкості, явну різницеву схему називають умовно стійкою, оскільки вона стійка при певному обмеженні на відношення просторово-часових кроків h і а саме: де В той же час, неявна різницева схема вільна від таких обмежень.

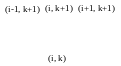
Як вже відмічалось раніше, неявну різницеву схему отримують шляхом апроксимації (заміни) похідної лівостороньою скінченою різницею по відношенню до вузла ( ), де апроксимують тільки на шарі, тобто шаблон неявної різницевої схеми має вигляд літери “Т” (рис.2.). Отже,

після апроксимації похідних , і підставляючи їх в рівняння теплопровідності (7.2), апроксимуючи початкові і граничні умови (7.4) отримаємо неявну різницеву схему

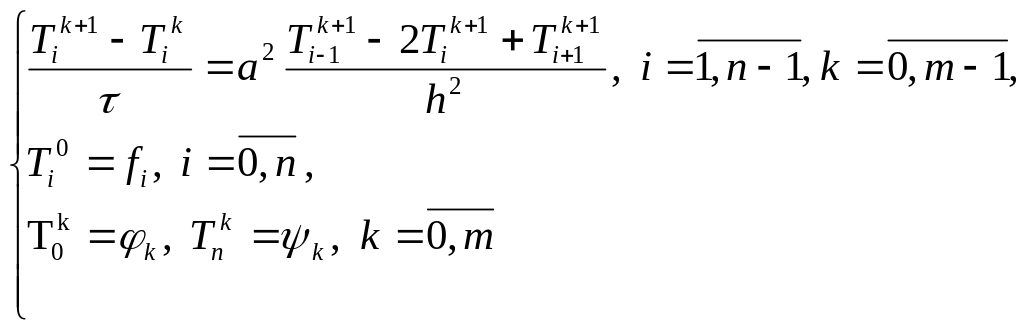
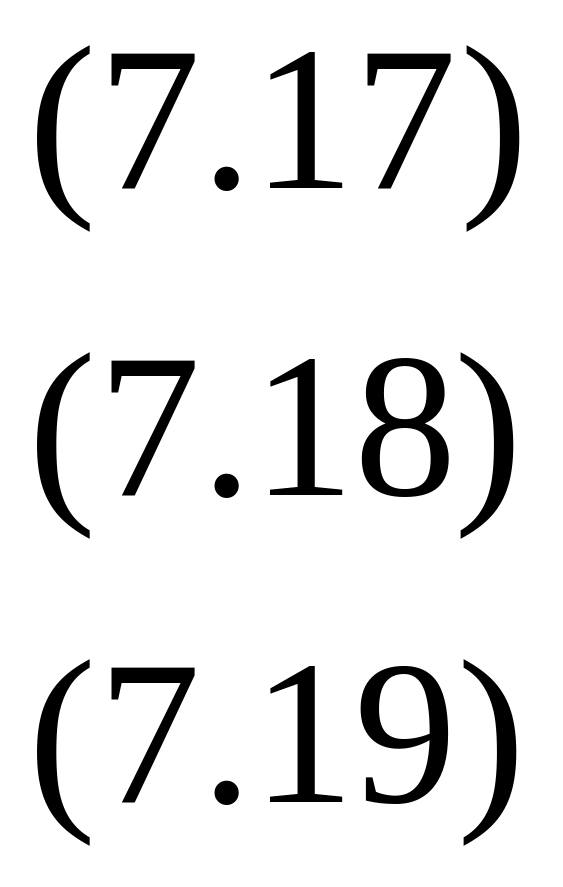
В теорії різницевих схем доведено, що дана неявна різницева схема (7.17) - (7.19) є стійкою при будь-яких кроках h і і називається абсолютно стійкою. Порядок її апроксимації , тобто 1-й по і 2-й – по h. Розв’язок даної різницевої схеми знаходиться послідовним обчисленням температури на часових шарах, починаючи з першого ( ). При цьому розв’язок на кожному часовому шарі знаходять методом прогонки, який є однією з модифікацій методу Гаусса розв’язування системи лінійних алгебричних рівнянь. В (7.17) невідомою є температура на шарі, і відомою на k-му шарі. Для цього приведемо схему (7.19) до так званого прогоночного вигляду:

де

Різницева схема (7.20)-(7.21) називається неявною різницевою схемою.

Розглянемо спеціальні методи розв’язання систем з трьохдіагональною матрицею. Цей метод називається методом прогонки. Тут - прогоночні коефіцієнти обчислені на часовому шарі .

(7.22)

Згідно цього методу розв’язок даної різницевої схеми пов’язаний з розв’язком СЛАР і набагато складніший, ніж розв’язок явної різницевої схеми, але якщо розглянути (7.20) неважко показати, що матриця буде трьохдіагональною. І розв’язок будемо шукати у вигляді

. (7.23)

Справа в тому, що на кожному часовому шарі доводиться виконувати свою прогонку, тобто розв’язувати СЛАР на кожному шарі по часу. Підставивши (7.23) в (7.20), отримаємо:

,

звідси отримаємо

.

Остання рівність можлива лише в тому випадку, коли

,

Звідки легко знаходимо прогоночні коефіцієнти

Формули (7.22) є рекурентними. Щоб обчислити значення прогоночних коефіцієнтів користуючись формулами (7.22), потрібно мати значення коефіцієнтів , які легко знаходяться із граничних умов (7.21). Використовуючи (7.23) і (7.21) маємо

Таким чином розв’язок неявної різницевої схеми (7.20)-(7.21) використовує метод прогонки і він дає формули (7.22), (7.23), (7.25). Для інших краєвих задач розв’язок дається формулами (7.22), (7.23), але інші. Тобто маємо

,

Прогоночні коефіцієнти обчислюються в результаті прямого ходу прогонки. В результаті зворотного ходу прогонки, обчислюємо по формулі (7.23) в кожній точці стержня на даному часовому шарі (в певний момент часу).

Зауваження 1. На кінцях стержня можуть задаватися різні граничні умови (І-ІІІ роду).

В зв’язку з цим неявна різницева схема (7.20) – (7.22) в більш загальному вигляді запишеться так:

де коефіцієнти ₁, ₂, , визначаються тим чи іншим чином в залежності від задання граничних умов І роду, коли задано розподіл температури на кінцях стержня

маємо

для граничних умов ІІ роду, коли на кінцях стержня задано теплові потоки,

(7.28)

маємо

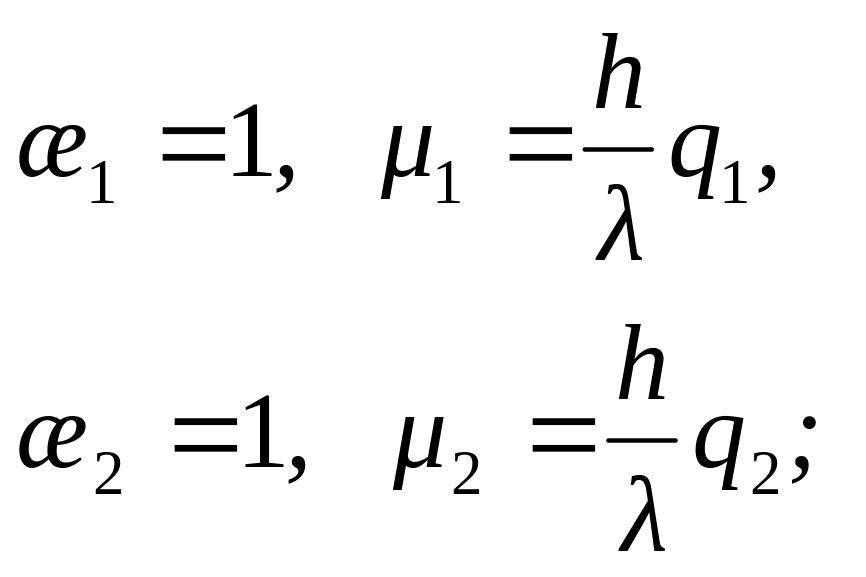(7.29)

Якщо співставити (7.27) і (7.28), то про гоночні коефіцієнти

(7.30)

Ці формули справедливі для задання будь-яких граничних умов.

для граничних умов ІІІ роду, тобто коли наявний теплообмін між стержнем і навколишнім середовищем

де - температура оточуючого середовища, маємо

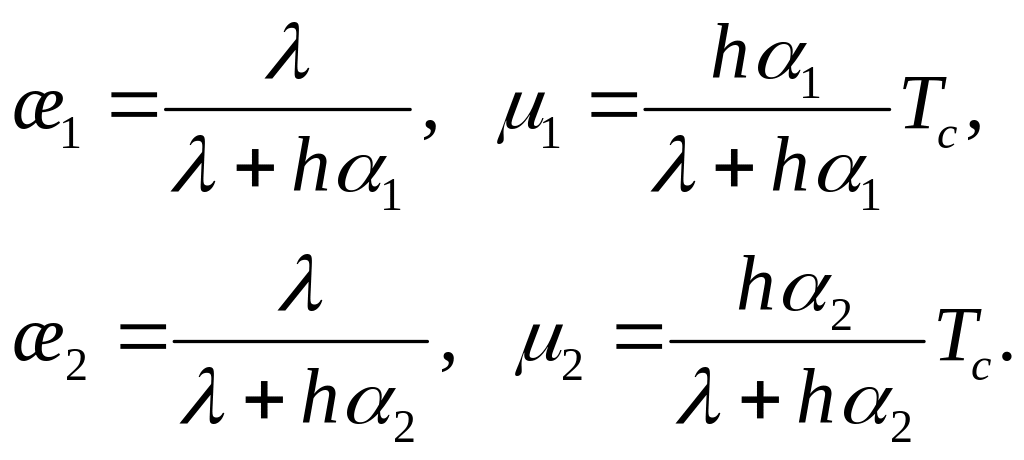(7.31)

Прогоночні коефіцієнти для всіх випадків граничних умов, обчислюються за формулами (7.23), причому

(7.32)

У випадку задання граничної умови ІІ або ІІІ роду на правому кінці стержня для проведення прогонки по формулах (7.22) потрібно знайти температуру . З формул (7.22) і (7.20), (7.27) маємо

Звідки знаходимо :

(7.32)

Зауваження 2. З теорії відомо, що для можливості застосування методу прогонки, достатньо, щоб виконувались умови