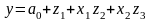- •1.Методи побудови моделей. Параметри об’єкта.
- •2.Оператор об’єкта. Визначення поняття ідентифікації.
- •3. Поділ моделей за способом їх побудови.
- •4. Класифікація моделей за видом оператора.
- •5.Класифікація об’єктів за числом потоків
- •6 Аналітичний метод побудови опису об'єкта.
- •7. Модель ідеального перемішування
- •8. Модель ідеального витіснення
- •9.Дифузійна модель
- •10.Побудова емпіричної лінії регресії
- •11.Коефіцієнти кореляції
- •12.Оцінка зв’язку між параметрами
- •13. Нелінійна регресія.
- •14. Мнк для ідентифікації об’єктів.
- •15. Застосування мнк до нелінійної регресії та багатомірного об’єкта.
- •16. Побудова лінії регресії засобами MatLab.
- •17. Процедура ідентифікації Ident програми Mat Lab.
- •18. Повний та дробовий факторні експерименти ідентифікації об’єктів.
- •19. Планування експериментів засобами MatLab.
- •20.Апроксимація та інтерполяція даних в MatLab.
- •21. Метод Брандона ідентифікації об’єкта
- •22.Перевірка адекватності моделі за методом Фішера
- •23.Загальна характеристика методів оптимізації моделі
- •24.Аналітичні методи оптимізації. Оптимізація об’єктів за методом Лагранжа
- •25. Загальна схема динамічної ідентифікації параметрів моделі.
- •26. Ідентифікація моделі динамічногго об’єкта.
- •27. Ідентифікація з використання моделей Вольтера.
- •28. Загальна характеристика активної ідентифікації.
- •29.Планування активного експерименту.
- •30. Ідентифікація об’єкта за перехідною характеристикою.
- •31.Визначення параметрів передаточної функції об’єкта за кривою розгону логарифмічним методом
- •32. Ідентифікація об’єкта за імпульсною перехідною характеристикою.
- •33.Індентифікація об’єктів за частотними характеристиками
- •34.Індентифікація перехідної характеристики з використанням методів площ.
- •35.Ідентифікації моделей об’єктів третього порядку за їх часовими характеристиками
- •36.Індентифікація об’єктів за загальною передаточною функцією
- •37. Моделювання теплообмінників.
- •38. Моделювання котельної установки
- •39. Функції та графіки середовища MatLab
- •40. Побудова та аналіз моделей в MatLab
- •41 Створення м-файлів в середовищі Matlab.
- •42 Блоки Matlab дослідження динамічних об’єктів.
- •43. Моделювання об’єктів автоматизації в Матлаб.
- •44. Моделі електричних машин в Матлаб.
10.Побудова емпіричної лінії регресії
У
випадку одномірного об’єкта за
експериментальними даними будується
графічна залежність між вхідним Х і
вихідним У параметрами, яка наз. емпірична
лінія регресії.Метожика побудови такої
лінії наступна: Наносимо точкі х і у в
сист. координат. Сис. Кординат з нанесеними
експериментальними даними наз. полем
кореляції.Розбиваємо по осі х на рівні
інтервали
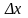 .
В кожному з
інтервалів знаходимо середнє значення
у за співвідношенням
.
В кожному з
інтервалів знаходимо середнє значення
у за співвідношенням
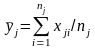 де k
— число інтервалів розбивки,
де k
— число інтервалів розбивки,
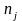 — число точок в інтервалі.
— число точок в інтервалі.
В результаті в кожному з інтервалів отримаємо по одній точці
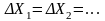 Отриманы
точки зєднуємо відрізками прямої,
отримана крива наз. Емпіричною лінією
регресії. За формою даної лінії роблять
попередні припущення чи може бути модель
обєкта задана лін. або нелін. рівнянням.
Проводять оцінку ступення звязку між
параметрами обєкта Х і У методом
кореляційного аналізу.
Отриманы
точки зєднуємо відрізками прямої,
отримана крива наз. Емпіричною лінією
регресії. За формою даної лінії роблять
попередні припущення чи може бути модель
обєкта задана лін. або нелін. рівнянням.
Проводять оцінку ступення звязку між
параметрами обєкта Х і У методом
кореляційного аналізу.
11.Коефіцієнти кореляції
Для оцінки ступення лінійного зязку між вх. вих. параметрами використовують коефіцієнт кореляції. Величина такої залежності між 1 вх. і 1 вих параметром вимірюється через простий коеф. кореляції, а між декількома вх. і 1 вих через множинний коеф. кореляції. Для визначення коеф. корел. необхідно на об’єкті провести деяку кількість експериментів. У випадку 1 вх. і 1 вих параметрів застосовують формулу для простого коеф. кореляції.
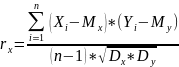
Mx і Mу – матем. середні по х і у
Dx і Dy –дисперсія
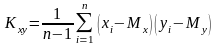 - другий
змішаний момент
- другий
змішаний момент
Тоді
простий коеф. корел.
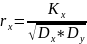
Множинний коеф. корел
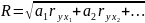
12.Оцінка зв’язку між параметрами
Коефіцієнт кореляції rxy Rxy можуть приймати значення від 0 до 1
Якщо дорівнює 0 то це вказує на відсутність лінійного зв’язку між вх. і вих. параметрами, якщо rxy Rxy близькі до 1то між вх. і вих. Параметом існує лінійна залежність.
Тобто для встановлення існування лінійної залежності між вх. вих. Параметром необхідно на об’єкті провести експерименти, та застосувати формули для простого або множиного коеф. кореляції.
13. Нелінійна регресія.
Якщо
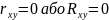 ,
то між вхідним та вихідним параметром
існує нелінійна залежність, тоді
емпірична лінія регресії носить
нелінійний характер і називається
нелінійною
регресією.
Тоді функціональна залежність y=f(x)
носить нелінійний характер: подальше
дослідження такої залежності є
трудомістким. У даному випадку цю
залежність необхідно перетворити до
лінійної за допомогою певних підстановок,
наприклад, якщо маємо залежність
,
то між вхідним та вихідним параметром
існує нелінійна залежність, тоді
емпірична лінія регресії носить
нелінійний характер і називається
нелінійною
регресією.
Тоді функціональна залежність y=f(x)
носить нелінійний характер: подальше
дослідження такої залежності є
трудомістким. У даному випадку цю
залежність необхідно перетворити до
лінійної за допомогою певних підстановок,
наприклад, якщо маємо залежність
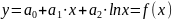 , тоді можна ввести наступні підстановки:
, тоді можна ввести наступні підстановки:
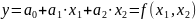
В
даному випадку від функцій з 2 змінними
прийняли за функції 2 змінних. Основна
трудність у випадку нелінійної регресії
полягає у підборі підстановок. Такий
перехід використовують перестановки
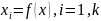 перетворюють початкову функцію у лінійну
і відповідає переходу під вихідних
змінних
перетворюють початкову функцію у лінійну
і відповідає переходу під вихідних
змінних
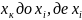 -
називається лінеаризуючими змінними,
а весь процес – лінеаризацією. На
практиці підстановки для переходу до
лінеаризуючих змінних шукають, як
правило, виходячи з фізики процесу.
Наприклад, при дослідженні швидкості
деякої хімічної реакції від концентрації
компонентів та температури, отримаємо
наступну функціональну залежність:
-
називається лінеаризуючими змінними,
а весь процес – лінеаризацією. На
практиці підстановки для переходу до
лінеаризуючих змінних шукають, як
правило, виходячи з фізики процесу.
Наприклад, при дослідженні швидкості
деякої хімічної реакції від концентрації
компонентів та температури, отримаємо
наступну функціональну залежність:
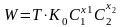
Для переходу до лінійного співвідношення треба про логарифмувати:
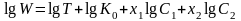
Введемо підстановки:

В результаті отримаємо ДР для дослідження: