7. Модель ідеального перемішування

Дана модель відноситься до типової двополюсної моделі.

Модель ідеального перемішування відповідає реальним потокам у проточних апаратах з мішалкою, у яких висота мало відрізняється від діаметра, а саме: . У даному випадку у всіх точках апарата концентрація є однаковою, що надходить в апарат, миттєво перемішується за допомогою мішалки і концентрація в апараті та на виході є однаковою.

Позначимо через х, у, y_ап відповідно об'ємний вміст речовини на вході, виході й всередині апарата. Через витрати. В загальному випадку в апараті буде акумулюватися наступна кількість речовини:

. (1)

Віднесемо дану кількість до всього об’єму апарата :

. (2)

Продиференціюємо ліву та праву частини рівняння зміни такого параметра:

. (3)

Дане рівняння описує динаміку зміни речовини в апараті. Аналогічно за формулою отримується р-ння якщо розгл. зміну іншого параметра, а саме розподіл температури у потоці теплоносія і структурою ідеального перемішування, таке р-ння має вигляд:

,

де Т_x — температура на вході апарата.

Т – температура в будь-якій точці апарата.

8. Модель ідеального витіснення

Дана модель відноситься до типової двополюсної моделі. Модель ідеального витіснення описує апарати трубчасті в яких l/d > 20 при цьому приймається для руху рідини, що Re > 2320, Re – число Рейнольдца. При даній умові буде наявний турбулентний рух оскільки за умови l/d > 20 поздовжнє перемішування є незначне, а при турбулентному русі за перерізом апарата відбувається рівномірний розподіл концентрації речовини.

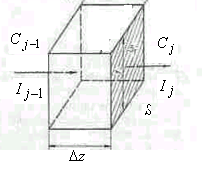
Рис.1

Рис.2

Розгл. рух деякої речовини в апараті довжиною l (рис.1) на перерізі

Z концентрація приймається однакова. Для складання математичного опису розглянемо деяку елементарну ділянку апарата за перерізом z довжиною (рис.2). Приймаємо, що площа перерізу S₁ =1, , де - лінійна швидкість речовини, -витрата

Об єм ділянки . При цьому в даному об ємі буде постійно знаходитись деяка кількість речовини ∆ М, яку можна записати у вигляді:

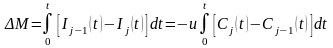
Розділимо ліву і праву частину на об єм даної зони:

,

=∆

Проінтегруємо даний вираз в результаті матимемо:

Оскільки _то (1)

_{В результаті отримали р-ння моделі ідеального витіснення. Дане р-ння виводилось на основі умови, що зміна концентрації} рівна змінні концентрації на відстані

9.Дифузійна модель

Більш складна - дифузійна модель широко застосовується при оцінці реальних потоків в апаратах, де відбувається подовжнє перемішування. Розрізняють одно - параметричну і дво - параметричну дифузійні моделі. Якщо враховують тільки поздовжнє перемішування, а в радіальному напрямку приймають рівномірний розподіл концентрації речовини, таку модель називають одно - параметричною дифузійною. Параметром, що характеризує одно - параметричну дифузійну модель, служить коефіцієнт подовжнього перемішування . У дво – параметричній є коефіцієнт радіального перемішування , визначається лише експериментальним шляхом. Тому на практиці використовують одно параметричну модель рівняння дифузійної моделі має вид:

Коли = 0, одно параметрична модель переходить у модель ідеального витіснення.