36.Індентифікація об’єктів за загальною передаточною функцією

Нехай передаточна функція об’єкта має вигляд:

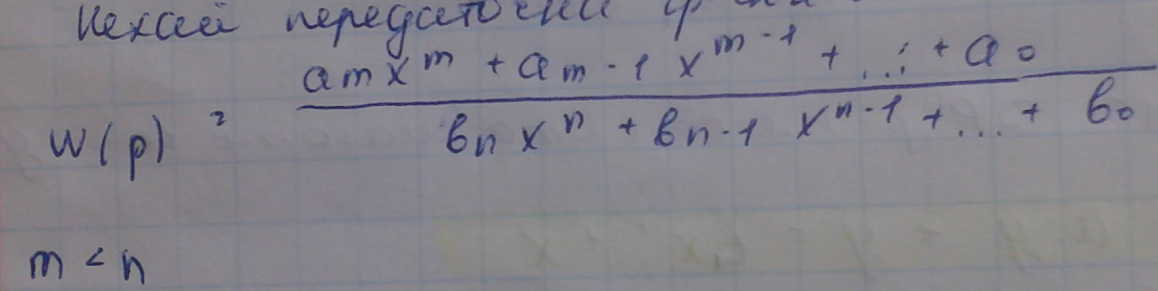
В задачах ідентифікації полягає у визначені коеф: a_i,b_j ;

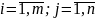
Для цього на початку як відомо по отриманій кривій розгону проводять її нормування коеф a_i,b_j встановлюються із наступної с-ми рівнянь:

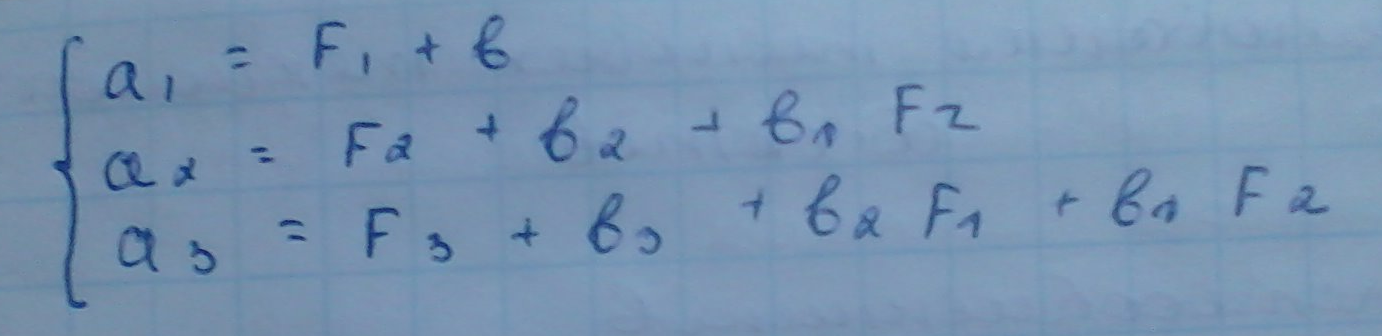
Інші коефіцієнти a_i,b_j що не увійшли в дану систему визначаються за аналогічними співвідношеннями, однак на практиці для об’єктів автоматизації обмежуються передаточними функціями максимально 3-тього роду.

Функції F₁ ,F₂ ,F_3, розраховуються за методом площ і визначаються за співвідношеннями:

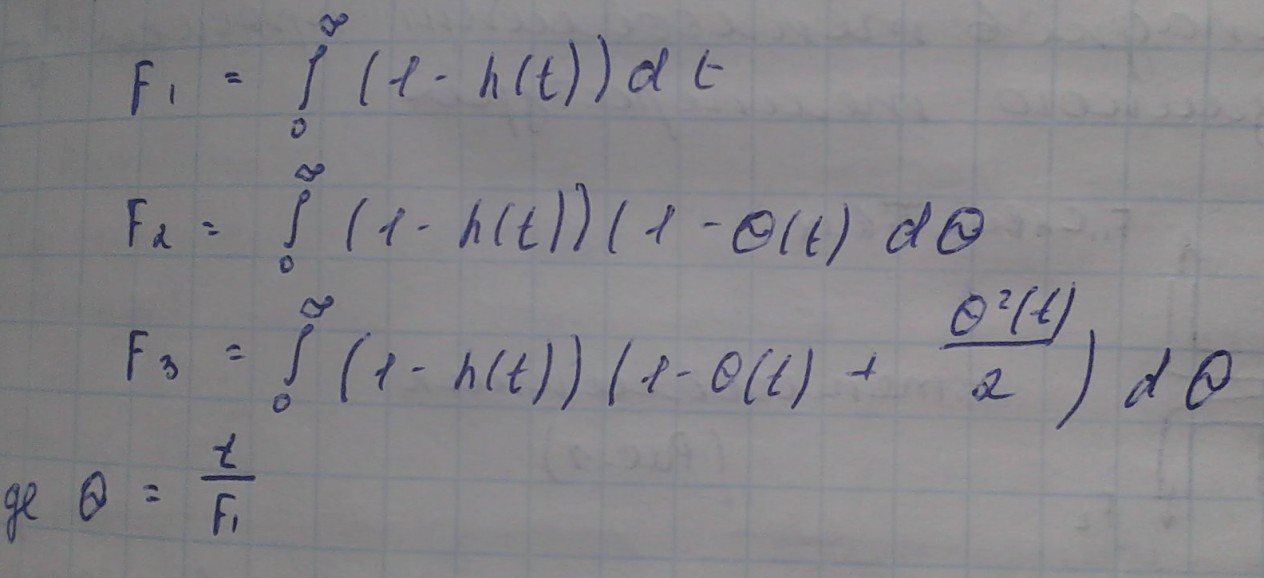
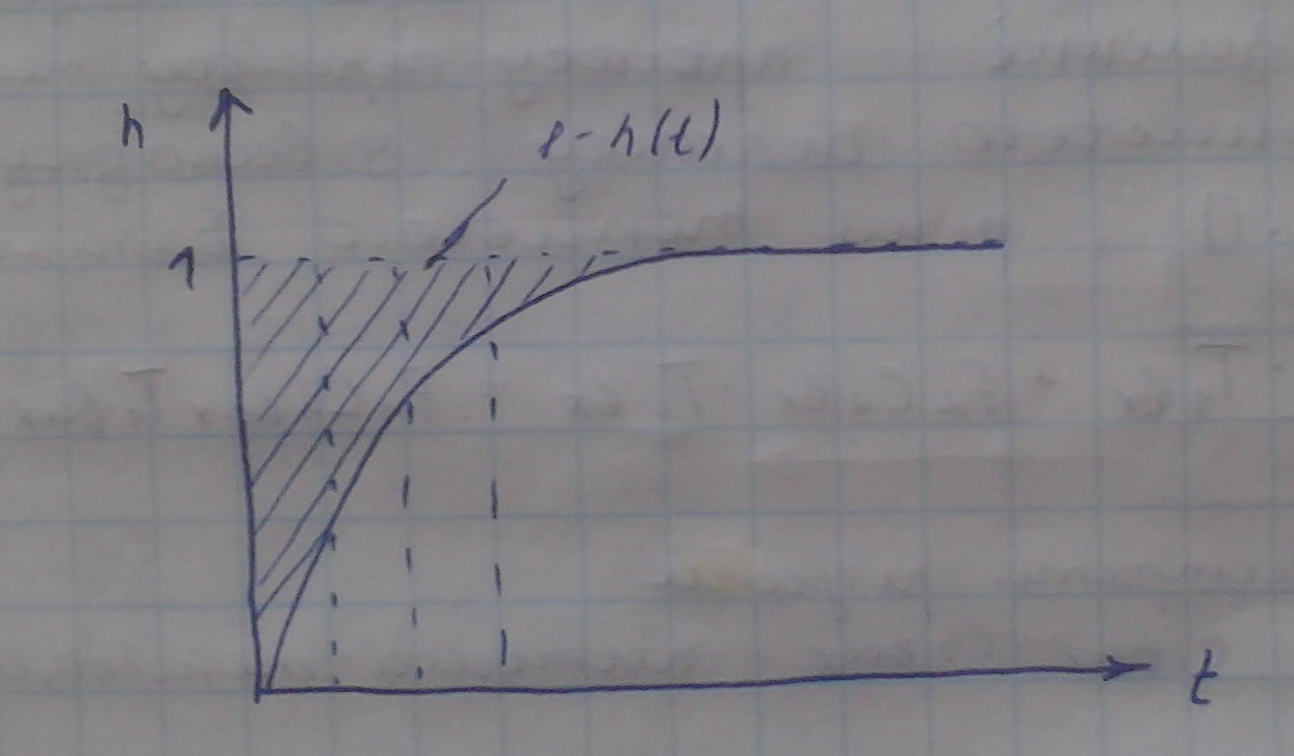
Для більш простого і точного розрахунку інтеграли замінюють сумами, а саме вісь х розбивають на рівні проміжки і обраховуються загальна площа, кожної з ділянок, при чому на кожній із ділянок відрізок перехідної х-ки замінюється прямою, тобто вводиться якась к-сть проміжків і така лінія замінюється кривою

37. Моделювання теплообмінників.

Моделі тепло- і масообмінних процесів створюються на основі окремих блоків, кожен з яких характеризується своїми параметри. Кожен блок моделі може мати різну ступінь деталізації, але параметри всіх блоків повинні знаходитися у взаємній відповідності. В більшості випадків тепломасообмінні процеси супроводжуються зміною температури.

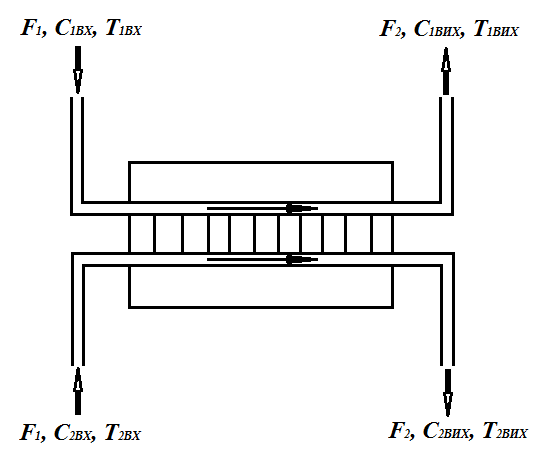
Основні змінні процесу переносу тепла зв’язані рівнянням теплового балансу. У випадку двох теплоносіїв (як на малюнку), рівняння теплового балансу:

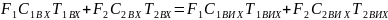
F₁ i F₂ – витрати рідини;

С₁ і С₂ – питома теплоємність на вході і виході.

Крім рівняння теплового балансу для опису теплообмінних процесів використовують рівняння теплопередачі від одного носія до іншого:

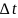– час перебування рідини в теплообміннику;

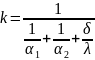
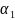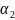і – коефіцієнти теплопередачі першого і другого теплоносія;

λ – коефіцієнт теплопровідності;

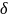– товщина стінок;

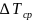– середня рівзниця температур, яка називається рушійною силою теплообмінного процесу.

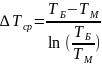
– різниця більших температур;

– різниця менших температур.

Дане рівняння показує яка кількість тепла передається від гарячого теплоносія до холодного за певної рушійної сили теплообмінного процесу.

За вказаними вище рівняннями теплового балансу та рівняннями теплопередачі не можна безпосередньо визначити як зміниться температура на виході із теплообмінника, якщо змінилась температура одного із теплоносіїв. У випадку двох теплоносіїв:

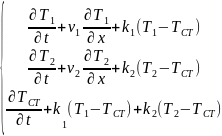
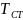– температура стінки площі теплопередачі;

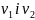- швидкості теплоносіїв;

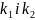- коефіцієнти, що пропорційні коефіцієнтам теплопередачі.

Дане рівняння є досить складним для отримання аналітичного розв’язку, а тому для їх розв’язку використовують числові методи.

38. Моделювання котельної установки

В загальному падку котел має три параметри і один вихідний:

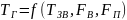
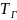– температура гарячої води;

– температура зворотної води;

– витрата води через котел;

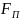– витрата палива.

При цьому будемо розглядати котел, як об’єкт з трьома незалежними вхідними параметрами – 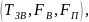і одним вихідним параметром – .

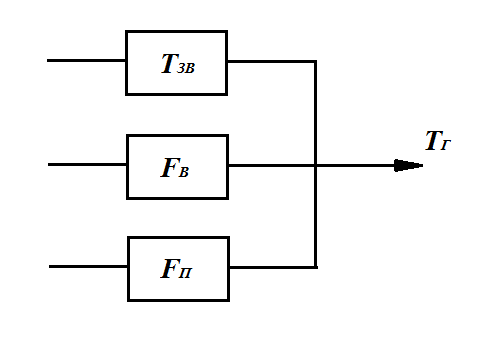
Побудуємо статичну характеристику котла – залежність виділеної з топки котла кількості тепла від кількості палива:

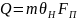(1)

m – ККД топки котла;

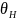- нижча теплотворна здатність палива (теплота згорання, яка не враховує виділення від конденсації).

- кількість палива, яка йде на підігрів води.

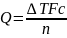(2)

n – ККД котла.

Прирівнюємо (1) та (2):

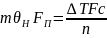
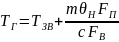
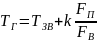(3)

Де .

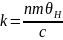Рівняння (3) – статична характеристика котла за трьома вхідними параметрами.

Як бачимо, температура гарячої води прямопропорційна температурі зворотньої води, а також прямопропорційна витраті палива і обернено пропорціна витраті води при сталій температурі зворотньої води.

Для побудови динамічної характеристики котла необхідно знайти повний диференціал від рівняння (3):

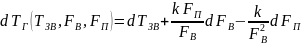
Температура води на виході із котла буде різнитися від температури на вході на час деякого запізнення, тому:

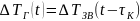
Як відомо, передаточна функція для такої ланки має вигляд:

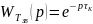(4)

Передаточні функції за ланками по витраті палива та витраті води можуть бути знайдені лише експериментальним шляхом. Як відомо з результатів експериментів, передаточна функція по витраті палива є аперіодичною ланкою ІІ порядку, а по витраті поди – аперіодичною ланкою І порядку, і відповідно мають вигляд:

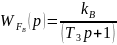
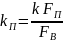
Отже, загальна передаточна функція котла матиме вигляд:

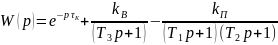
Сталі часу можуть бути знайдені за методами, описаними вище. (де блять?)