4. Эффективные физико-механические характеристики волокнистых композитов. Численные результаты, сравнительный анализ

4.1. Макроскопически ортотропная трехфазная гетерогенная среда. Эффективные модули Юнга, коэффициенты Пуассона, коэффициенты линейного температурного расширения и модули сдвига

4.1.1. Свойства компонентов. Эффективный модуль Юнга в направлении волокон. Рассмотрим однонаправленный волокнистый упругий композит с двоякопериодической структурой, компоненты которого идеально связаны между собой. Представительный элемент объема (ячейка периодичности) рассматриваемой гетеро­генной среды изображен на рис.2.1. Гетерогенная среда состоит из трех фаз (компонентов) матрицы m и включений f₁, f₂ ; в роли включений f₂ выступают каналы. Свойства матрицы m и волокон f₁ (модуль Юнга E, коэффициент Пуассона n и ко­эффициент линейного температурного расширения a) приведены в таблице 4.1; объемные концентрации компонентов: . Заметим, что среда является существенно гетерогенной:

Таблица 4.1

Свойства компонентов

		m	f1
E	МПа
n	–	0,4000	0,3500
a	K–1

Используя данные таблицы 4.1, определим эффективный модуль Юнга в направлении волокон (3.1.3):

МПа (4.1.1)

4.1.2. Основные параметры конечно-элементных моделей и систем конечно-элементных уравнений. Для решения задач микромеханики композиционных материалов согласно алгоритму 1.4 применим метод конечных элементов. При решении задач использу­ется различные конечно-элементные модели, каждая из которых имеет наименование:

, (4.1.2)

где – количество узлов конечного элемента, используемых для аппроксимации неизвестного поля ( – линейный, – квадратичный четырехугольные изопараметрические [36] элементы);

– общее количество элементов;

– общее количество узлов.

Важнейшим моментом конечно-элементного анализа является решение системы линейных алгебраических уравнений. Поэтому в дальнейшем, наряду с основными параметрами конечно-элементных моделей , приводятся и основные характеристики систем конечно-элементных уравнений:

n – количество уравнений;

– максимальная ширина ленты (b_i – локальная ширина ленты – число элементов в i-ой строке матрицы, начиная с первого ненулевого и кончая диагональным);

– профиль матрицы.

4.1.3. Эффективные модули Юнга и кoэффициeнты Пуассона. Для конечно-элементного решения задач (1) и (2) о поперечном растяжении ячейки периодичности при задании кинематико-статических граничных условий (3.1.4), (3.1.5) используем две конечно-элементные модели:

М–8/40/153 – КЭ-модель 1-го уровня;

М–8/160/545 – КЭ-модель 2-го уровня, полученная из КЭ-модели 1-го уровня делением каждого конечного элемента на четыре конечных элемента.

В таблице 4.2 представлены основные параметры используемых конечно-элементных моделей и соответствующих им систем ко­нечно элементных уравнении. На рис.4.1 изображена конечно-элементная модель М–8/160/545 части ячейки периодичности.

Таблица 4.2

Основные параметры конечно-элементных моделей и систем конечно-элементных уравнений

Модель	n	b	p
М–8/40/153	306	120	12 111
М–8/160/545	1090	428	82 199

Решим указанные задачи, принимая . Компоненты средних тензоров микронапряжений представлены в табли­це 4.3.

Таблица 4.3

Средние напряжения в задачах о поперечном растяжении (МПа)

Задача	Модель
(1)	М–8/40/153	32,27	12,64	16,27
(1)	М–8/160/545	32,26	12,66	16,27
(2)	М–8/40/153	12,64	36,21	17,62
(2)	М–8/160/545	12,66	36,19	17,62

Из приведенных результатов следует:

1. Средние напряжения практически не изменились при пере­ходе от КЭ-модели 1-го уровня к КЭ-модели 2-го уровня (так называемое сгущение конечно-элементной сетки, “h”-сходимость)

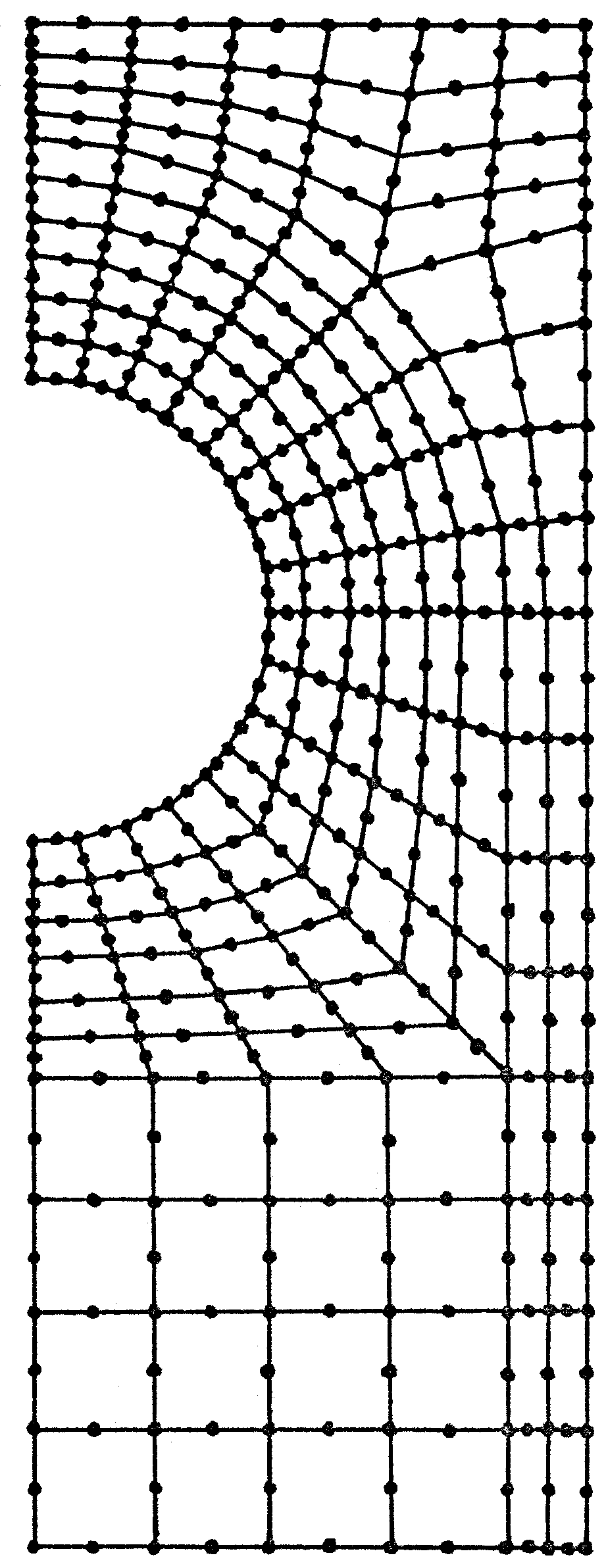
Рис. 4.1. Конечно-элементная модель

2. Выполняется теорема взаимности Бетти:

Определим эффективные модули Юнга и коэффициенты Пуас­сона, используя соотношения (3.1.9), (3.1.10), (4.1.1) и средние напряжения из таблицы 4.3 (модель M-8/160/545);

4.1.4. Эффективные коэффициенты линейного температурного расширения. Решим задачу о равномерном нагреве ячейки периодичности при задании кинематико-статических граничных условий (3.2.3). Используем КЭ-модель 2-го уровня – M–8/160/545. Компоненты среднего тензора микро­напряжений имеют следующие значения:

Используя соотношения (3.2.5), определим эффективные коэффициенты линейного температурного расширения:

4.1.5. Эффективные модули сдвига. Для определения эффективного модуля сдвига решим задачу о поперечном сдвиге ячейки периодичности, находящейся в плоском деформированном состоянии, при задании кинематико-статических гра­ничных условий (3.4.12). Используя соотношение (3.4.15), определим эффективный модуль сдвига :

Для определения эффективных модулей сдвига решим две задачи о продольном сдвиге ячейки периодичности (антиплоская деформация) при задании смешанных граничных условий (3.4.16) и (3.4.20). Используя соотношения (3.4.19) и (3.4.21), определим эффективные модули сдвига :

Отметим, что при решении указанных задач о попереч­ном сдвиге и продольном сдвиге использовались две конечно-элементные модели: M–8/40/153 и М–8/160/545; средние напряжения при переходе от КЭ-модели 1-го уровня к КЭ-модели 2-го уровня изменяются лишь в четвертой значащей цифре.

4.2. Макроскопически трансверсально-изотропная двухфазная гетерогенная среда. Эффективные модули Юнга, коэффициенты Пуассона, коэффициенты линейного температурного расширения и модули сдвига

4.2.1. Представительный элемент объёма. Свойства компонентов. Эффективный модуль Юнга в направлении волокон. Рассмотрим однонаправленный волокнистый упругий композит с двоякопериодической структурой, компоненты которого идеаль­но связаны между собой. Представительный элемент объема (ячейка периодичности) рассматриваемой гетерогенной среды изображен на рис.4.2. Гетерогенная среда состоит из двух фаз (компонентов): матрицы m и включений (волокон) f. Свойства матрицы m и волокон f приведены в таблице 4.1; объемные концентрации компонентов: .

Отметим, что гетерогенная среда двоякопериодической структуры, составленная из ячеек периодичности, изображен­ных на рис.4.2, является макроскопически трансверсально-изотропной средой.

Используя данные таблицы 4.1, определим эффективный модуль Юнга в направлении волокон (3.1.3):

4.2.2. Эффективные модули Юнга и коэффициенты Пуассона. Для конечно-элементного решения задачи (1) о поперечном растяжении ячейки периодичности при задании кинематико-статических условий (3.1.4) используем две конечно-элементные модели:

M–8/64/221 – КЭ-модель 1-го уровня;

М–8/256/825 – КЭ-модель 2-го уровня.

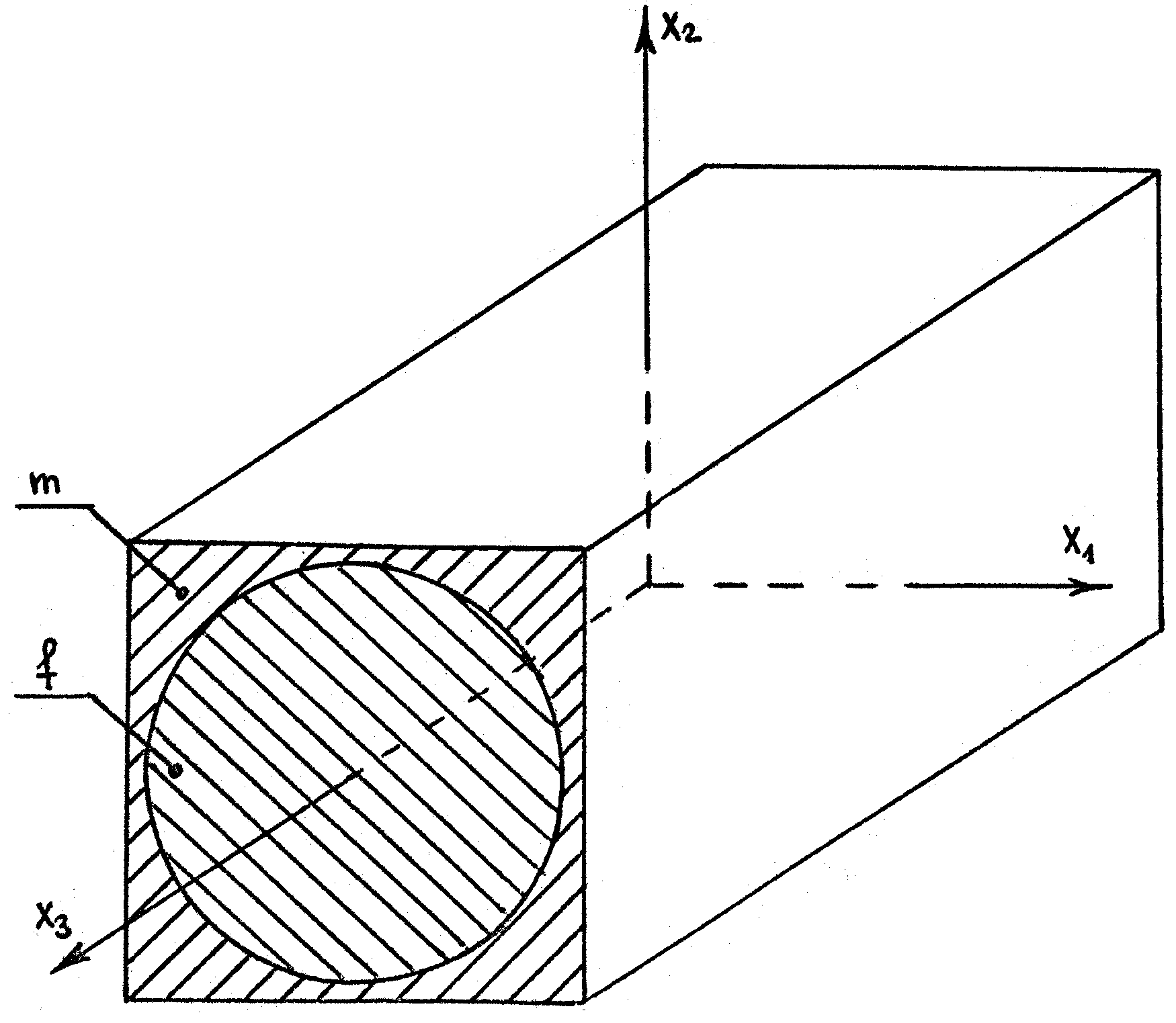
Рис. 4.2. Представительный элемент объема (ячейка периодичности)

В таблице 4.4 представлены основные параметры используемых конечно- элементных моделей и соответствующих им систем конечно-элементных уравнений. На рис.4.3 представлена конечно-элементная модель М–8/256/825 части ячейки периодичности.

Таблица 4.4