
- •31.Параметричні і канонічні рівняння прямої у просторі. Рівняння прямої ,що проходить через дві точки.
- •32 . Кут між прямими . Умови паралельності і перпендикулярності двох прямих у просторі. .
- •33.Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини.
- •34.Криві другого порядку. Рівняння кола.
- •35. Еліпс. Вивід канонічного рівняння еліпса, ексцентриситет та директриси еліпса. Найпростіші властивості еліпса
- •Директриса та ексцентриситет
- •36. Гіпербола . Вивід канонічного рівняня гіперболи, ексцентриситет , директриси та асимптоти гіперболи.
- •37. Парабола. Вивід канонічного рівняння.
- •38.Числова послідовність. Означення границі послідовності. Нескінченно малі та нескінченно великі величини. Зв’язок між нескінченно малими і нескінченно великими величинами.
- •39.Означення границі функції. Односторонні границі. Леми про нескінченно малі величини.
- •Односторонні границі. Ліва та права границя функції
- •40. Арифметичні дії над функціями , що мають скінченні границі. Важливі границі.
39.Означення границі функції. Односторонні границі. Леми про нескінченно малі величини.
Визначення границі функції
Нехай
функція
![]() визначена
на деякій підмножині
визначена
на деякій підмножині
![]() множини
дійсних чисел
множини
дійсних чисел
![]() ,
і
,
і
![]() –
гранична точка множини
.
Нагадаємо, що у будь-якому
–
гранична точка множини
.
Нагадаємо, що у будь-якому
![]() –околі
–околі
![]() граничної
точки
міститься нескінченне число точок
множини
, проте сама точка
може
й не належати
.
граничної
точки
міститься нескінченне число точок
множини
, проте сама точка
може
й не належати
.
Визначення
1.
(Гейне).
Число
![]() називається
границею функції
називається
границею функції![]() при
при![]() (або в точці
),
якщо для довільної послідовності
(або в точці
),
якщо для довільної послідовності
![]() ,
збіжної до
,
відповідна послідовність значень
функції
,
збіжної до
,
відповідна послідовність значень
функції
![]() збіжна
до
.
збіжна
до
.
Якщо
число
–
границя функції в точці
,
то пишуть
![]() або
або
![]() при
.
при
.
Нехай функція має границю , тоді вона, очевидно, єдина. Це випливає з того, що збіжна послідовність може мати лише одну границю (див. гл.5, §1).
Визначення
2.
(Коші). Число
називається
границею функції
при
(або
в точці
),
якщо для будь-якого
![]() можна
знайти таке число
можна
знайти таке число
![]() ,
що при всіх
,
що при всіх
![]() ,
які задовольняють нерівність
,
які задовольняють нерівність
![]()
виконується нерівність
![]()
Визначення границі функції в точці за Гейне і за Коші еквівалентні.
Відзначимо
геометричний зміст визначення 2,
скориставшись графіком функції
(рис.40
). Який би малий
–окіл
точки А не взяти, повинен існувати такий
![]() –окіл
точки
,
що коли
–окіл
точки
,
що коли
![]() змінюється між
змінюється між
![]() і
і
![]() ,
графік функції
знаходиться у смузі шириною
,
графік функції
знаходиться у смузі шириною
![]() між прямими
між прямими
![]() .
Підкреслимо, що в точці
функція
може
набувати значення, яке не дорівнює А,
або навіть бути невизначеною. Тому в
визначенні 2 йдеться саме про нерівність
.
Підкреслимо, що в точці
функція
може
набувати значення, яке не дорівнює А,
або навіть бути невизначеною. Тому в
визначенні 2 йдеться саме про нерівність
![]()
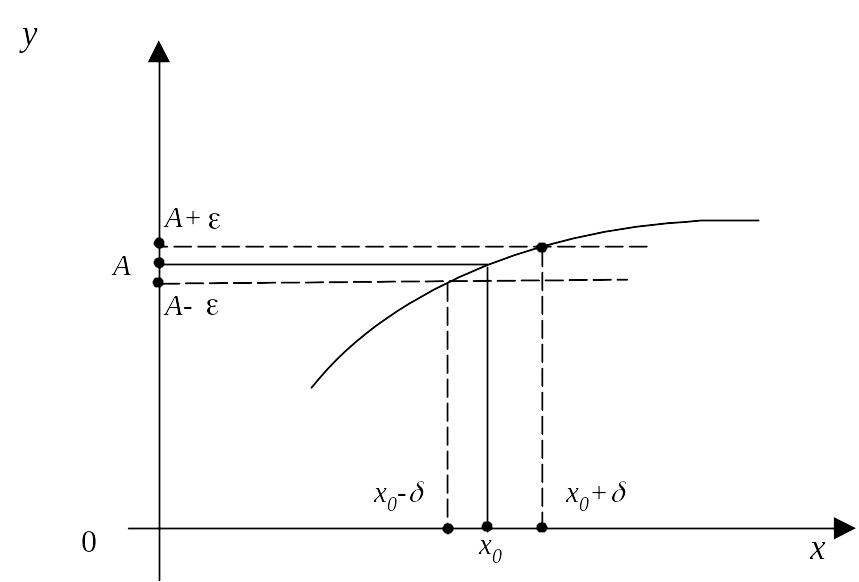
Рис.43
Односторонні границі. Ліва та права границя функції
Нехай
функція
![]() визначена
на проміжку
визначена
на проміжку
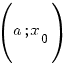 .
Число
.
Число
![]() називають
лівою
границею функції
в
точці
називають
лівою
границею функції
в
точці
![]() і
пишуть
і
пишуть
![]() ,
,
якщо для
будь-якого числа
![]() знайдеться
додатнє число
знайдеться
додатнє число
![]() ,
яке залежить від
,
яке залежить від
![]() ,
таке, що для всіх
,
таке, що для всіх
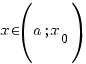 ,
які задовільняють нерівність
,
які задовільняють нерівність
![]() ,
виконується нерівність
,
виконується нерівність
![]() .
.
Аналогічно визначається права границя функції . Для позначення правої границі функції в точці використовується позначення
![]() .
.
Ліва і права границі функції називаються односторонніми границями.
40. Арифметичні дії над функціями , що мають скінченні границі. Важливі границі.
Деякі важливі границі:
- Границя частки одиниці і х дорівнює нулю, якщо х прямує до нескінченності.
- Границя частки синуса х і х дорівнює одиниці, якщо х пярмує до нуля.
