35. Еліпс. Вивід канонічного рівняння еліпса, ексцентриситет та директриси еліпса. Найпростіші властивості еліпса

Властивість 1. Еліпс має що найменше дві осі симетрії і центр симетрії.

□ Дійсно,  якщо точка  належить еліпсу в канонічній системі координат, тобто , то і точки ,  і  належать еліпсу. А це означає, що осі координат канонічної системи координат є осями симетрії еліпса, а її початок координат – центром симетрії. ■

Зауваження. Можна показати, що еліпс, який не є колом має рівно дві осі симетрії.

 

Властивість 2. Еліпс перетинає осі симетрії у чотирьох точках.

□ В канонічній системі координат точки перетину еліпса з осями симетрії знаходяться з рівнянь  і  і мають, відповідно, координати , , , . ■

Означення. Точки перетину еліпса з осями симетрії називаються вершинами еліпса.

Властивість 3. Еліпс є обмеженою фігурою, він міститься у прямокутнику зі сторонами  і .

З рівняння еліпса маємо:  і , або  і . Останні нерівності визначають прямокутник зі сторонами  і . ■

Отриманої інформації достатньо, щоб зобразити еліпс у канонічній системі координат, користуючись його властивостями. У I чверті дуга еліпса визначається рівнянням 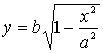, тобто є графіком деякої функції (рис. 19).

Скористувавшись наявністю двох осей симетрії, побудуємо увесь еліпс (рис. 20 і рис. 21). Параметри  і  називають півосями ( ‑ більшою,  ‑ меншою). Вони дорівнюють половинам відстаней між відповідними протилежними вершинами еліпса.

Форму еліпса характеризує параметр . Він є коефіцієнтом стиснення кола, з якого можна отримати еліпс шляхом стиснення або розтягування. Більш зручним у дослідженнях є параметр 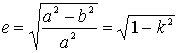. Він називається ексцентриситетом еліпса. Ексцентриситет кола дорівнює 0.

Канонічне рівняння еліпса

Директриса та ексцентриситет

Число це ексцентриситет еліпса, величина, що характеризує його витягнутість; для еліпсу . Прямі, рівняння яких називаються директрисами еліпса; співвідношення відстані від будь-якої точки еліпса до найближчого фокусу до відстані до найближчої директриси стале і дорівнює ексцентриситету.

Зауважимо, що величинами, які характеризують еліпс, є велика і мала півосі і , відстань фокуса від центру, ексцентриситет . Залежність між ними виражається формулами: . Тому, щоб скласти рівняння еліпса, досить знати або півосі і , або одну піввісь і ексцентриситет і т.д.

Якщо точки і збігаються, то еліпс стає колом радіуса . При цьому . Отже, коло є окремим випадком еліпса.

36. Гіпербола . Вивід канонічного рівняня гіперболи, ексцентриситет , директриси та асимптоти гіперболи.

Найпростіші властивості гіперболи

Властивість 1. Гіпербола має щонайменше дві осі симетрії і центр симетрії.

Властивість 2. Гіпербола перетинає одну з осей симетрії в двох точках, які називаються вершинами; з другою віссю симетрії гіпербола не перетинається.

Точки перетину знаходяться з рівнянь , . Тому вершинами гіперболи в канонічній системі координат є точки , .

Властивість 3. Гіпербола має асимптоти, тобто прямі, до яких гіпербола необмежено наближається.

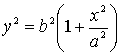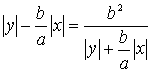Розглянемо гіперболу в канонічній системі координат: . Тоді , а . Якщо  набуває великі значення, то  мало відрізняється від . Тому відстань від точок гіперболи до прямої , або до прямої , прямує до нуля, якщо точки гіперболи прямують до нескінченності.

Побудуємо гіперболу, скориставшись її властивостями. У I чверті дуга гіперболи визначається рівнянням 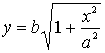 і має вигляд, показаний на рис. 22. Використовуючи осі симетрії гіперболи, отримаємо її повністю (рис. 23  

Параметри  і  також називають півосями гіперболи,  ‑ дійсною,  ‑ уявною.

Канонічне рівняння гіперболи.

Гіпербола є невиродженою кривою другого порядку, яка задається рівнянням

де та  — параметри. Таке рівняння називається канонічним рівнянням гіперболи

Нехай канонічне рівняння кривої другого порядку шляхом переносу центру координат перетворено у вигляд:

В цьому випадку крива проходить через початок координат нової системи; вісь абсцис є віссю симетрії кривої. Це рівняння відображає той факт, що невироджена крива другого порядку є геометричним місцем точок, відношення відстаней яких (ексцентриситет) від заданої точки (фокуса) та від заданої прямої (директриса) незмінна. Крива є гіперболою, якщо Тобто, гіпербола є геометричним місцем точок, абсолютна величина різниці відстаней яких від фокусів дорівнює (фокальна властивість гіперболи). Директоріальна властивість гіперболи полягає в тому, що гіпербола є геометричним місцем точок, відношення відстаней яких від фокуса до одноіменної директриси дорівнює .

Ексцентриситет (позначається лат. e або грец. ε) — числова характеристика конічного перерізу, яка показує ступінь його відхилення від кола, і дорівнює відношенню відстаней:

• від будь-якої точки конічного перерізу до фокусу та

• від цієї точки до директриси.

Два конічні перерізи, які мають однаковий ексцентриситет, є подібними.

• Для кола ексцентриситет вважають рівним нулю;

• Для еліпса ексцентриситет більший нуля та менший за одиницю (що більший ексцентриситет, то «витягнутіший» еліпс);

• Ексцентриситет параболи дорівнює одиниці;

• Ескцентриситет гіперболи більший за одиницю.

Для еліпсу та гіперболи ексцентриситет можна визначити як відношення фокальної відстані до великої або дійсної вісі.

Параметр 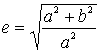 називається ексцентриситетом. Він характеризує форму гіперболи.

Асимпто́та криво́ї (грец. ασυμπτωτος — що не збігається, не дотикається) — це пряма, до якої крива при видаленні в нескінченність наближається як завгодно близько.

Якщо крива, задана рівнянням y = f(x), віддаляється в нескінченність при наближення x до скінченної точки a, то пряма x = a називається вертикальною асимптотою цієї кривої.

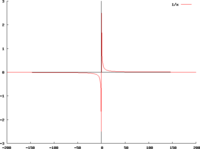
f(x)=1/x

Такими асимптотами є пряма x = 0 для гіперболи y = 1/x кожна з прямих x = kπ (k = 0, ± 1, ± 2, …) для функції у = ctg(x).

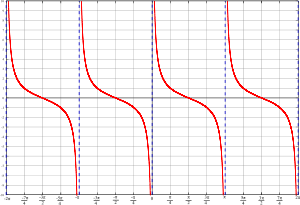
f(x)=ctg(x)

Крім вертикальної асимптоти x = 0 гіпербола y = 1/x має ще й горизонтальну асимптоту у = 0, як і графік функції у = е^-x sin(х), проте він, на відміну від гіперболи, перетинає свою горизонтальну асимптоту нескінченну кількість раз (+графік).

Криві, що описуються рівняннями х³ + у³ — Заху = 0 (декартів лист) (+графік), та у = 1/х + х мають похилу асимптоту.

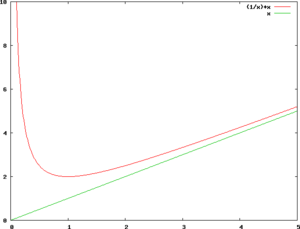
f(x)=1/x+x

Коефіцієнти k і b в рівнянні прямої у = kx + b — похилої асимптоти кривої у = f(x) при віддаленні до плюс чи мінус нескінченності, знаходять як границі:

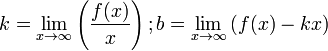
Горизонтальна асимптота є частковим випадком похилої при k = 0. Дослідження асимптот дозволяє чіткіше уявити поведінку графіка функції, оскільки властивості функції поблизу її асимптоти дуже близькі до властивостей асимптоти — лінійної функції, властивості якої добре вивчені. Систематичне використання цієї властивості породило напрямок у сучасній математиці — «асимптотичні методи дослідження».

Не всі криві мають асимптоти. Наприклад парабола асимптот не має.