- •31.Параметричні і канонічні рівняння прямої у просторі. Рівняння прямої ,що проходить через дві точки.
- •32 . Кут між прямими . Умови паралельності і перпендикулярності двох прямих у просторі. .
- •33.Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини.
- •34.Криві другого порядку. Рівняння кола.
- •35. Еліпс. Вивід канонічного рівняння еліпса, ексцентриситет та директриси еліпса. Найпростіші властивості еліпса
- •Директриса та ексцентриситет
- •36. Гіпербола . Вивід канонічного рівняня гіперболи, ексцентриситет , директриси та асимптоти гіперболи.
- •37. Парабола. Вивід канонічного рівняння.
- •38.Числова послідовність. Означення границі послідовності. Нескінченно малі та нескінченно великі величини. Зв’язок між нескінченно малими і нескінченно великими величинами.
- •39.Означення границі функції. Односторонні границі. Леми про нескінченно малі величини.
- •Односторонні границі. Ліва та права границя функції
- •40. Арифметичні дії над функціями , що мають скінченні границі. Важливі границі.
33.Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини.
Кутом
між прямою та площиною
називається кут між цією прямою і її
проекцію (ортогональною) на площину.
Якщо
пряма перпендикулярна до площини, то
кут між нею й площиною вважається таким,
що дорівнює
,
а між паралельними прямою та площиною
таким, що дорівнює
![]() .
Кут
між прямою та площиною і кут між цією
прямою й перпендикуляром до площини в
сумі дорівнюють
.
На
рисунку
.
Кут
між прямою та площиною і кут між цією
прямою й перпендикуляром до площини в
сумі дорівнюють
.
На
рисунку
![]() .
.
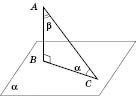
Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.
Теорема
2. Якщо
пряма паралельна площині, то на цій
площині знайдеться пряма, яка паралельна
даній прямій. Зверніть
увагу:
паралельність прямої і площини не
означає, що ця пряма паралельна будь-якій
прямій на цій площині. Кожна пряма цієї
площини буде або паралельна даній, або
мимобіжна з нею.
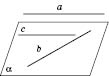
На рисунку:
![]() ;
;
![]() ;
;
![]() ;
a і b — мимобіжні;
;
a і b — мимобіжні;
![]() .
.
Теорема
3. Через
точку, що не лежить на площині, можна
провести безліч прямих, паралельних
даній площині, причому всі вони лежать
в одній площині (паралельній даній).
Теорема 4. Якщо площина перетинає одну
з двох паралельних прямих, то вона
перетинає й другу пряму (див. рисунок).
На рисунку
![]() .
.
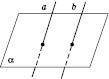 Дві
площини називаються паралельними, якщо
вони не перетинаються.
Дві
площини називаються паралельними, якщо
вони не перетинаються.
Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, що лежить у площині і проходить через точку перетину.
Теорема 1. Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.
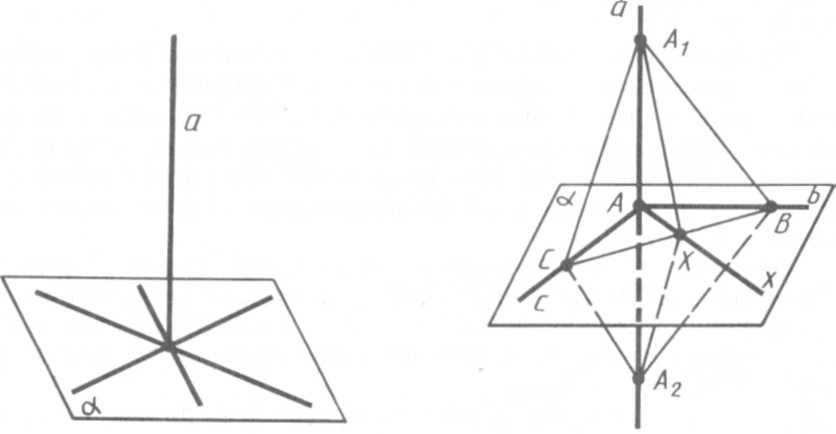
Мал. 3 Мал. 4
Доведення.
Нехай а
—
пряма,
перпендикулярна до прямих бісу
площині ![]() .
.
Тоді пряма а проходить через точку А перетину прямих b і с (мал. 4). Доведемо, що пряма а перпендикулярна до площини .
Проведемо
довільну пряму х
через
точку А
у
площині а
і
покажемо, що вона перпендикулярна до
прямої а.
Проведемо
у площині
довільну
пряму, яка не проходить через точку А
і
перетинає прямі
b,
с
і
х.
Нехай
точками перетину будуть В,
С
і
X. Відкладемо
на прямій а
від
точки А
в
різні боки рівні відрізки: ![]() і
АА2.
Трикутник
і
АА2.
Трикутник
![]() рівнобедрений,
оскільки відрізок АС
є
висотою за умовою теореми і медіаною —
за
побудовою (
=АА2).
З
тієї ж причини трикутник
рівнобедрений,
оскільки відрізок АС
є
висотою за умовою теореми і медіаною —
за
побудовою (
=АА2).
З
тієї ж причини трикутник ![]() теж
рівнобедрений. Отже, трикутники
теж
рівнобедрений. Отже, трикутники ![]() і
А2ВС
рівні
за третьою ознакою рівності трикутників.
і
А2ВС
рівні
за третьою ознакою рівності трикутників.
З
рівності трикутників
і
А2ВС
випливає
рівність кутів ![]() ВХ,
А2ВХ
і,
отже, рівність трикутників
ВХ
i
А2ВХ
за
першою ознакою рівності трикутників.
З рівності сторін
Х
і
А2Х
цих
трикутників робимо висновок, що трикутник
ХА2
рівнобедрений.
Тому його медіана ХА
є
також висотою. А це означає, що –
пряма
х
перпендикулярна
до
.
За
означенням пряма а
перпендикулярна
до площини а
.
Теорему
доведено.
ВХ,
А2ВХ
і,
отже, рівність трикутників
ВХ
i
А2ВХ
за
першою ознакою рівності трикутників.
З рівності сторін
Х
і
А2Х
цих
трикутників робимо висновок, що трикутник
ХА2
рівнобедрений.
Тому його медіана ХА
є
також висотою. А це означає, що –
пряма
х
перпендикулярна
до
.
За
означенням пряма а
перпендикулярна
до площини а
.
Теорему
доведено.
34.Криві другого порядку. Рівняння кола.
Лінія другого порядку – це множина точок, координати яких задовольняють рівняння вигляду
![]()
![]() ,
,
де
![]() –
дійсні числа, причому хоча б одне з чисел
–
дійсні числа, причому хоча б одне з чисел
![]() відмінне
від нуля. Зокрема, до ліній другого
порядку належать такі лінії: коло, еліпс,
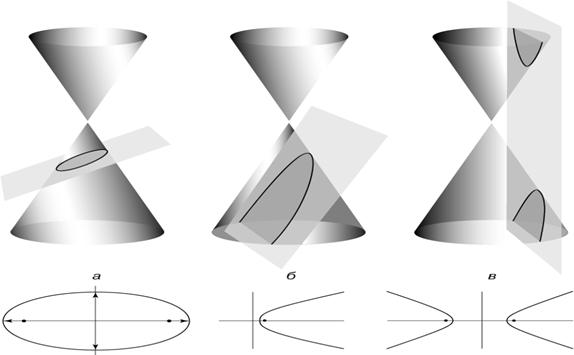
гіпербола і парабола. Лінії другого
порядку називають також конічними
перетинами через те, що їх можна дістати
як лінії перетину кругового конуса з
площиною (рис. 27).
відмінне
від нуля. Зокрема, до ліній другого
порядку належать такі лінії: коло, еліпс,
гіпербола і парабола. Лінії другого
порядку називають також конічними
перетинами через те, що їх можна дістати
як лінії перетину кругового конуса з
площиною (рис. 27).
|
Алгебраїчне означення
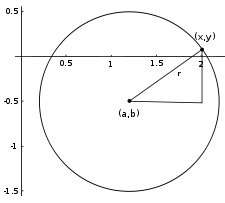
![]()
Коло радіуса r = 1, з центром (a, b) = (1.2, -0.5)
Коло
на площині, даного радіуса
![]() ,
у певній вибраній декартовій
системі координат
,
у певній вибраній декартовій
системі координат
![]() і
і
![]() ,
з центром в точці (a,
b)
описується стандартним рівнянням:
,
з центром в точці (a,
b)
описується стандартним рівнянням:
![]()
Це рівняння випливає з теореми Піфагора, при її застовуванні до кожної точки кола, як показано на рисунку справа, де радіус це гіпотенуза прямокутного трикутника, катети якого x − a та y − b. Якщо центр кола знаходиться в початку координат (0, 0), тоді рівняння спрощується до такого вигляду:
![]()
Загальне рівняння кола:
![]()
Якщо
відомі координати трьох точок на площині
![]()
![]() і
і
![]() ,
то рівняння кола, яке проходить через
ці точки можна записати через визначник:
,
то рівняння кола, яке проходить через
ці точки можна записати через визначник:
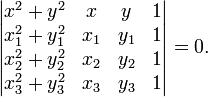
Параметричне означення
Коло на площині, даного радіуса , у певній вибраній декартовій системі координат і , описується системою рівнянь:
![]()
![]()
де
параметр
![]() —
пробігає значення від
—
пробігає значення від
![]() до
до
![]() .
З геометричної точки зору це кут до осі
x,
променя проведеного з початку координат
до точки (x, y).
Якщо записати x
та y
через параметр t,
отримаєм:
.
З геометричної точки зору це кут до осі
x,
променя проведеного з початку координат
до точки (x, y).
Якщо записати x
та y
через параметр t,
отримаєм:
![]()
![]()
Полярні координати
Рівняння кола в полярних координатах:
![]()
де a – радіус кола, r0 - відстань від початку координат до центру кола та φ – кут відкладений проти годинникової стрілки від додатньої осі x до лінії що з’єднує початок координат з центром кола. Для кола, центр якого знаходиться в початку координат r0 = 0, це рівняння спрощується до вигляду r = a. Якщо r0 = a або якщо початок координат лежить на колі, тоді отримуєм рівняння:
![]() .
.
В загальному випадку, рівняння можна розв’язати для r:
![]() ,
,
Розвязок із знаком мінус перед коренем дає ідентичну криву.
Комплексна площина
Рівняння кола на комплексній площині:
![]()
або в параметричному вигляді
![]()