8.4. Цикл Карно

Рис. 8.4.1

Круговой процесс или цикл – это совокупность процессов, в результате которых система возвращается в исходное состояние. Если в круговом процессе совершается положительная работа, то цикл называется прямым (по часовой стрелке), если отрицательная – обратным (против часовой стрелки рис. 8.4.1).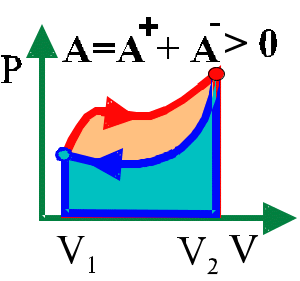

Рис. 8.4.2

 Принцип действия тепловых двигателей.

Тепловой двигатель превращает внутреннюю энергию топлива в механическую энергию (работу). Примеры: паровой или турбинный двигатель, двигатель внутреннего сгорания, двигатель Дизеля.

Тепловой двигатель состоит из нагревателя (котел, камера сгорания), холодильника (теплообменник, атмосфера) и рабочего тела (газ, пар). В рабочем цикле (рис.8.4.2) протекают следующие процессы:

 Рабочее тело получает от нагревателя теплоту Q₁ при температуре Т₁.

 Рабочее тело, расширяясь, совершает работу А₁.

 Для возвращения в начальное состояние, остаток теплоты Q₂ рабочее тело отдает холодильнику при температуре Т₂ < Т₁.

 Внешние силы доводят температуру и давление рабочего тела до начальных значений, совершая над ним работу .

КПД теплового двигателя  определяется отношением полезной работы (энергии) к затраченной. Применяя для рабочего тела закон сохранения энергии, получаем , тогда

_.

Тепловые двигатели с обратными циклами называются холодильниками. Для них , и . Противоестественный ход тепла (от холодного к горячему) обеспечивается внешней работой.



Рис. 8.4.3

Цикл Карно – идеальная модель кругового цикла.

Цикл Карно состоит из двух изотерм (1–1^/ , 2–2^/) и двух адиабат (1^/–2, 2^/ –1). Каждый из этих процессов идеален потому, что теплота и изменение внутренней энергии в них полностью превращаются в работу (рис.8.4.3).

Рассмотрим изменение энтропии рабочего тела.

Общее изменение энтропии в цикле . Так как мы рассматриваем только обратимые процессы, общее изменение энтропии .

—изменение энтропии при изотермическом расширении 1–1^/,

— адиабатное расширение с охлаждением до температуры холодильника ,

— изотермическое сжатие в контакте с холодильником тело отдает теплоту,

— адиабатное сжатие до начального состояния .

Общее изменение . Поэтому,

максимальный кпд теплового двигателя — .

 Следствия:

1. КПД цикла Карно не зависит от рода рабочего тела.

2. КПД определяется только разницей температур нагревателя и холодильника.

3. КПД не может быть равен 100% даже у идеальной тепловой машины, так как при этом температура холодильника должна быть , что запрещено законами квантовой механики.

4. Невозможно создать вечный двигатель второго рода, т.е. двигатель, работающий в тепловом равновесии без перепада температур при .

Глава 9 реальные газы

9.1. Уравнение состояния реальных газов (уравнение Ван–дер–Ваальса).

 Силы межмолекулярного взаимодействия.

а) Молекулы идеального газа (упругие материальные точки) не взаимодействуют друг с другом. Их внутренняя энергия не зависит от расположения молекул и определяется только их кинетической энергией. Такая модель описывает поведение весьма разряженных реальных газов и плохо работает в области больших давлений и фазовых переходов газ—жидкость.

Рис. 9.1.1

б) Изучение упругих свойства твердых тел и жидкостей показывает, что на близких расстояниях ( диаметров) молекулы отталкиваются, на расстояниях ( диаметров) — притягиваются, на расстояниях >9 диаметров взаимодействием молекул можно пренебречь. Силы межмолекулярного взаимодействия имеют электромагнитную квантовую природу. Примерная зависимость сил взаимодействия от межмолекулярного расстояния представлена на верхнем рисунке 9.1.1.

Рис. 9.1.2

На нижнем рисунке 9.1.2 представлена зависимость потенциальной энергии двух молекул ( ) от расстояния между ними ( ). Пунктирной линией отмечено положение равновесия, в котором потенциальная энергия достигает минимума.

Соотношение между потенциальной и кинетической энергией молекулы определяет агрегатное состояние вещества.

— газ, — жидкость, — твердое тело.

 Уравнение состояния реальных газов.

Уравнение состояния одного моля любого идеального газа справедливо для газов, в которых можно пренебречь размерами и взаимодействием молекул, что подходит для реальных разряженных газов. Однако, при относительно больших давлениях и низких температурах это не так.

1. Учтем конечный объем реальных молекул, обозначив его .

Тогда свободный молярный объем уменьшится: , следовательно . Так как, при , — собственный объем молекул.

2. Учтем взаимодействие молекул. За счет взаимного притяжения молекул давление на стенки сосуда уменьшится на : или

.

О

Рис. 9.1.3

пределим . Для этого представим объем газа в виде двух объемов

Рис. 3.2.3

(рис.9.1.3) с концентрациями . Силы притяжения первой и второй частей пропорциональны концентрации молекул в поверхностном слое на левой и правой поверхности границы раздела, поэтому , где параметр, зависящий только от природы газа, тогда:

— Уравнение Ван–дер–Ваальса.