15 Динамика механика

изучает механическое движение, то есть перемещение одних тел относительно других.

Глава 1. Кинематика

раздел механики, в котором изучается движение тел без выяснения причин этого движения.

1.1. Закон движения материальной точки

Материальная точка – тело, размером которого можно пренебречь в данной задаче (размеры тел намного меньше расстояний между ними; тела движутся поступательно).



Рис. 1.1.1

Система отсчета выбирается для описания движения тел. Система отсчета включает тело отсчета (относительно которого рассматривается движение), связанную с ним систему координат и способ отсчета времени (часы) (рис. 1.1.1).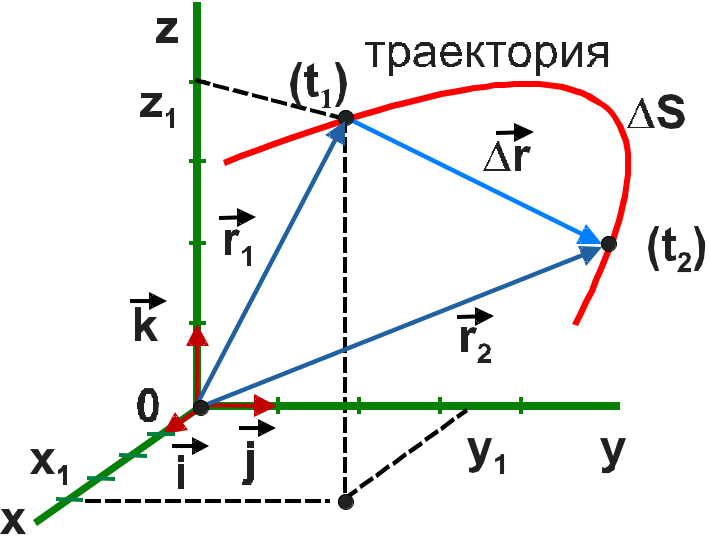

Положение материальной точки в пространстве задается радиусом–вектором , или его проекциями на оси (координатами ). Связь этих величин определяет формула , где – единичные векторы (орты) осей (рис. 1.1.1), причем, (теорема Пифагора).



или .

Закон движения представляет зависимость радиуса-вектора ( или координат ) от времени t и позволяет определить положение движущейся материальной точки в любой момент:

Эти соотношения связаны принципом суперпозиции движений: любое сложное движение в пространстве можно представить суммой трех независимых прямолинейных движений вдоль осей

Траектория – линия, по которой движется тело (рис. 1.1.1).

Путь (м) – расстояние, пройденное телом по траектории за время .

Перемещение (м) – вектор, соединяющий начальную и конечную точки пути: .

1.2. Скорость определяет быстроту движения.

 Математика.

Средней скоростью изменения функции называется отношение приращения функции к приращению аргумента :

.

Мгновенной, истинной скоростью изменения называется предел, к которому стремиться средняя скорость при :

. Таким образом,

Чтобы определить скорость изменения функции, надо взять производную этой функции по времени.

 Скорости движения определяют быстроту движения.

При движении материальной точки становятся функциями от времени , поэтому, вводится три типа скоростей:



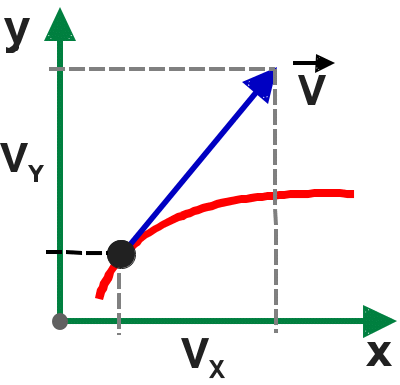Рис. 1.2.1

Мгновенная скорость (м/с) – первая производная радиуса-вектора по времени: .

Вектор мгновенной скорости направлен по касательной к траектории (рис. 1.2.1)

Координатные скорости – проекции вектора скорости на оси координат (рис. 1.2.1) – равны первой производной соответствующей координаты по времени: .

Скалярная, путевая скорость (м/с) – первая производная пути по времени: .

Связи между скоростями.

Дифференцируя принцип суперпозиции, получаем:

.

Так как , то .

Из теоремы Пифагора — .

1.3. Ускорение

определяет быстроту изменения скорости (скорость изменения скорости).

Аналогично скорости, можно ввести три типа ускорений.

Ускорение (м/с²) – первая производная скорости или вторая производная радиуса-вектора по времени :

.

Координатные ускорения – проекции вектора ускорения на оси координат:

.

 Связи между ускорениями.

Дифференцируя принцип суперпозиции два раза, получаем:

.

Из теоремы Пифагора: .



Рис. 1.3.1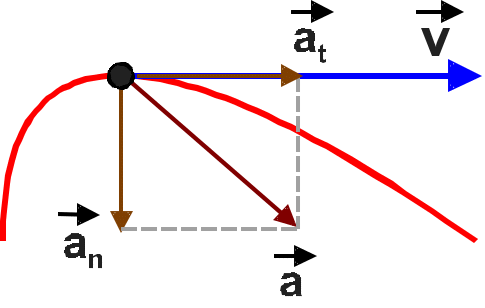

Тангенциальная и нормальная составляющие ускорения.

В общем случае ускорение направлено под любым углом к скорости . Поэтому, его удобно представлять векторной суммой двух ускорений (рис.1.3.1):

.

– тангенциальное ускорение – направлено вдоль (против) направления скорости и определяет изменение скорости движения материальной точки по величине:

.

– нормальное ускорение – направлено перпендикулярно скорости. Определяет изменение скорости материальной точки по направлению:

,

где – радиус кривизны траектории.