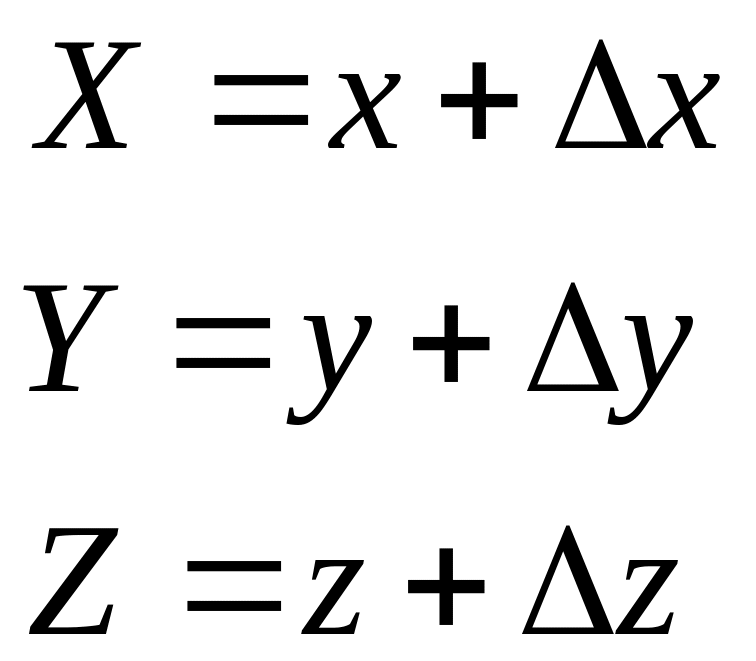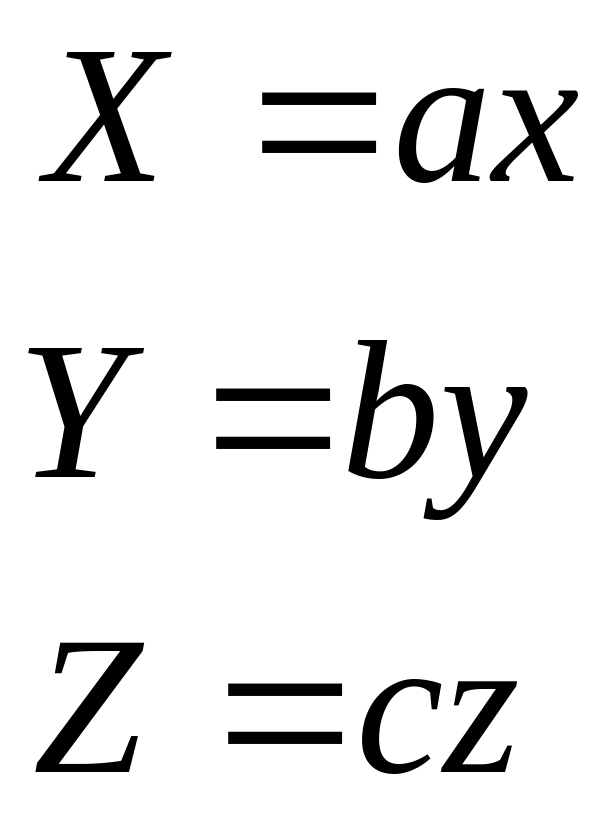Лекция № 8,9 координатные преобразование объектов.

Общие вопросы преобразования.

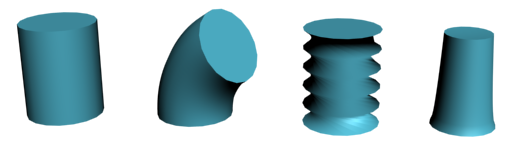
В компьютерной графике часто применяются различные геометрические преобразования над объектами: вращение, сжатие, параллельный перенос и др. С помощью них, однократно описав топологию объекта, мы можем получить много различных его экземпляров. Обычно принято разделять преобразования первого рода (собственные движения, сохраняющие ориентацию углов) и преобразования второго рода (зеркальные движения, меняющие ее). К первым относят параллельный перенос, поворот и др., ко вторым – симметрии (относительно точки, прямой, окружности). Математически эти преобразования описываются матрицами преобразований.

В качестве модели здесь выступает описание поверхности трехмерного объекта в виде некоторого подмножества точек декартова пространства. Поэтому рассматриваемые преобразования тесно связанны с системой координат. Координатный метод был введен в XVII веке французскими математиками Декартом и Ферма. В современ­ной компьютерной графике широко используется координатный метод. Это­му есть несколько причин:

• Каждая точка на экране (или на бумаге при печати на принтере) задается координатами (например, пиксельными).

• Координаты используются для описания объектов, которые будут ото­бражаться как пространственные. Например, объекты микромира, объек­ты на поверхности Земли, объекты космического пространства и тому по­добное.

• При выполнении многих промежуточных действий отображения исполь­зуют разные системы координат и преобразования из одной системы в другую.

Преобразование координат и преобразование объектов.

Сначала рассмотрим общие вопросы преобразования координат. Пусть зада­на n-мерная система координат в базисе (k₁, k₂, ..., k_n), описывающая положе­ние точки в пространстве с помощью числовых значений k_i. В компьютер­ной графике чаще всего используется двумерная (n=2) и трехмерная (n=3) системы координат. Если задать другую, N-мерную, систему координат в базисе (m₁, т₂, .... m_N) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует), можно записать в таком виде:

где f_i – функция пересчета i-й координаты.

Можно поставить и обратную задачу – по известным координатам (m₁, т₂, .... m_N) определить координаты (k₁, k₂, ..., k_n) . Решение обратной задачи запи­шем так:

где F_i – функции обратного преобразования.

В случае, когда размерности систем координат не совпадают (п  N), осуще­ствить однозначное преобразование координат зачастую не удается. Напри­мер, по двумерным экранным координатам нельзя без дополнительных усло­вий однозначно определить трехмерные координаты отображаемых объектов.

Преобразование объектов можно описать так. Пусть любая точка, которая принадлежит определенному объекту, имеет координаты (k₁, k₂, ..., k_n) в n-мерной системе координат. Тогда преобразование объекта можно опреде­лить как изменение положения точек объекта. Новое положение точки про­странства отвечает новым значениям координат (т₁, т₂ .... т_n).

Соотношение между старыми и новыми координатами для всех точек объек­та:

(т₁, т₂ .... т_n) = F(k₁, k₂, ..., k_n) и будет определять преобразование объ­екта,

где F – функция преобразования.

Например, преобразование объектов на плоскости можно определить так:

В трехмерном пространстве:

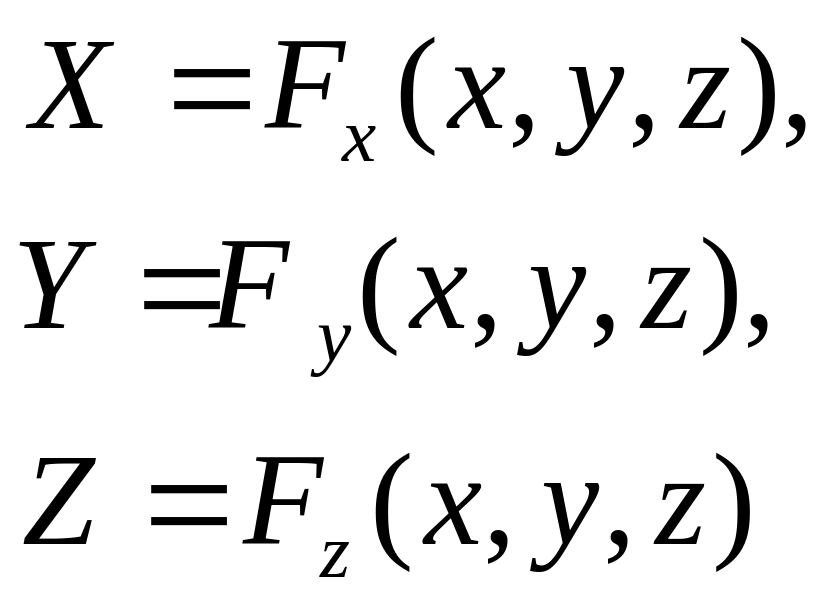
Классификация преобразований.

Преобразования классифицируют:

• по системам координат (например, преобразование из полярной систе­мы в прямоугольную);

• по виду функций преобразования f_i.

По виду функций преобразования различают линейные и нелинейные преоб­разования.

Если при всех i = 1, 2, .... N, функции f_i – линейные относительно аргументов (k₁, k₂, ..., k_n), то есть , где a_ij – константы, то такие преобразования называются линейными, а при п = N – аффинными.

Если хотя бы для одного i функция f_i – нелинейная относительно (k₁, k₂, ..., k_n), тогда преобразование координат в целом не линейно. Например, преобразование – нелинейное, так как в выражении для Y присутствует ху.

Примеры линейных и нелинейных преобразований.

Линейные преобразования (прямые переходят в прямые).

• Линейное преобразование применяется к каждой точке (вершине) модели;

• Не изменяет топологию модели.

Можно описать уравнением:

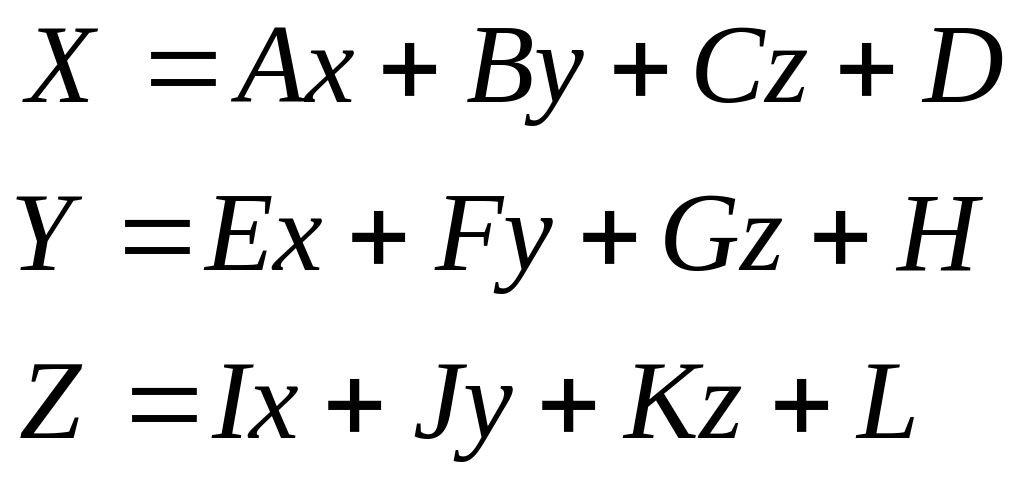
Перенос
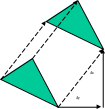
Параллельный перенос есть перемещение каждой точки в одном и том же направлении на фиксированное расстояние. Преобразование параллельного переноса задается следующими формулами:
Поворот (2D)
Поворот – это преобразование плоскости, при котором расстояние от центра поворота до точки сохраняется и каждая точка повернута на определенный ориентированный угол, т.е. движение с единственной неподвижной точкой.
Масштабирование
Преобразование подобия есть преобразование плоскости, при котором расстояния изменяются в некоторое фиксированное число раз (k).
Сдвиг (2D)

Нелинейные преобразования.

Произвольное преобразование точек модели