
- •010400.62 «Прикладная математика и информатика»
- •Введение
- •§1. Классификация интегральных уравнений
- •§2. Решение интегральных уравнений Фредгольма методом последовательных приближений
- •§3. Уравнения с вырожденными ядрами
- •§4. Решение интегральных уравнений Фредгольма с помощью ряда Неймана
- •§5. Итерированные ядра и резольвента интегральных уравнений Фредгольма
- •§6. Решение линейных интегральных уравнений Фредгольма второго рода методом последовательных подстановок
- •§7. Уравнение Фредгольма как предел системы конечного числа линейных алгебраических уравнений. Фундаментальные соотношения Фредгольма
- •§8. Доказательство сходимости рядов Фредгольма
- •§9. Решение интегрального уравнения, данное Фредгольмом при . Первая фундаментальная теорема Фредгольма
- •20…§10. Решение однородных интегральных уравнений. Вторая фундаментальная теорема Фредгольма
- •Вторая фундаментальная теорема Фредгольма
- •И их вычисление
- •§12. Вычисление собственных значений и собственных функций по методу Келлога
- •§13. Сопряжённые однородные интегральные уравнения
- •§23. Перед тем, как перейти к исследованию неоднородного интегрального уравнения при , рассмотрим однородное интегральное уравнение
- •§15. Теорема Адамара
- •§16. Обзор других методов решения. Приближённые методы решения
- •§16. Задачи для самостоятельного решения
- •Примерный вариант тест-контрольной работы
- •Литература
- •Оглавление
- •Тест-контрольная по интегральным уравнениям Вольтерра
- •1 Вариант
- •9.Записать решение уравнения, если резольвента ядра известна
- •Вариант
- •Вариант
- •Вариант
- •Вариант теста по интегральным уравнениям Вольтерра
- •Ответы к тестам по интегральным уравнениям Вольтерра
- •Блок1. Интегральные уравнения Вольтерра
И их вычисление
1.
Определения. Если
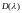 есть определитель Фредгольма для ядра
и
есть определитель Фредгольма для ядра
и
 то
называют собственным
значением
ядра
.
то
называют собственным
значением
ядра
.
Далее,
если
 непрерывна, не обращается тождественно
в нуль в интервале
непрерывна, не обращается тождественно
в нуль в интервале
 и удовлетворяет уравнению
и удовлетворяет уравнению

то называют собственной функцией ядра , принадлежащей собственному значению .
Функции
 образуют полную
систему
собственных функций ядра
принадлежащих собственному значению
,
если каждое другое решение выражается
линейно через эти q
решений. Таким образом, если
образуют полную
систему
собственных функций ядра
принадлежащих собственному значению
,
если каждое другое решение выражается
линейно через эти q
решений. Таким образом, если
 - какие-либо другие q
решений, то должны иметь место
q
соотношений
- какие-либо другие q
решений, то должны иметь место
q
соотношений

………….………………. ,

Если, кроме того,

то функции в свою очередь образуют другую полную систему собственных функций, принадлежащих .
Для строгого доказательства второй фундаментальной теоремы Фредгольма, а также для нахождения фундаментальных функций по формуле (10.4) необходимо определить миноры Фредгольма высших порядков
а) Определение p-го минора для .
P-й минор для , по определению, выражается рядом
, (30)(11.1)
который
при
p=1
приводится к
 где (29)
где (29)


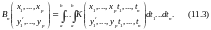
(28)
С помощью теоремы Адамара можно доказать, вполне аналогично тому, как мы делали это раньше, следующую теорему.
Теорема 9. Бесконечный ряд для абсолютно сходится для всех значений и равномерно относительно ; , удовлетворяющих неравенствам , .
Следствие. Если два значения x с различными индексами становятся равными, например , или же два значения y: , то обращается в нуль.
Действительно, тогда в определителе, стоящем в выражении (28) (11.3) для под знаком интеграла, две строки (два столбца) становятся одинаковыми. Поэтому
,
и, следовательно,
На таком же основании, если в переменить местами два или же два с разными индексами, то переменит знак.
§12. Вычисление собственных значений и собственных функций по методу Келлога
Выпишем
линейное интегральное уравнение
Фредгольма первого рода и рассмотрим
линейный интегральный оператор

 (11.4)
(12.1)
(11.4)
(12.1)
 -
вещественная и непрерывная функция,
при этом
-
вещественная и непрерывная функция,
при этом
 ядро симметрическое
ядро симметрическое
 .
.
Ранее
было доказано существование собственных
функций ядра
 удовлетворяющих этим требованиям.
Рассмотрим метод их конструктивного
определения, например, путем последовательных
приближений по методу Келлога.
удовлетворяющих этим требованиям.
Рассмотрим метод их конструктивного
определения, например, путем последовательных
приближений по методу Келлога.
Докажем, что собственные функции и собственные значения могут быть найдены методом последовательных приближений.
Возьмём произвольную непрерывную функцию
 ,
такую,
,
такую,
что
 и пусть
и пусть
 (11.2)
(11.5)
(12.2)
(11.2)
(11.5)
(12.2)
Обозначим
 ,
тогда
,
тогда
 ,
(11.3) (11.6)
(12.3)
,
(11.3) (11.6)
(12.3)
где
 .
.
Доказательство.
Пусть
 ,
а
,
а
 ,
тогда в силу симметрии оператора
,
тогда в силу симметрии оператора
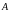 найдём
найдём

Для
нормированных
функций
 тогда из (12.2) имеем
тогда из (12.2) имеем
 откуда положив
откуда положив
 получаем
получаем
 (11.4)
(11.7)
(12.4)
(11.4)
(11.7)
(12.4)
Докажем сходимость последовательности
 .
.
Т.к.
 ,
то в силу неравенства Коши-Буняковского
,
то в силу неравенства Коши-Буняковского
 ,
тогда следует
,
тогда следует
 или
или
 и последовательность
- монотонно невозрастающая и ограничена
снизу, следовательно существует
и последовательность
- монотонно невозрастающая и ограничена
снизу, следовательно существует
 .
.
Покажем,
что
 ,
для этого, соотношение (12.2)
,
для этого, соотношение (12.2)
 умножим на
умножим на
 ,
проинтегрируем по
,
проинтегрируем по
 и воспользуемся неравенством
Коши-Буняковского.
и воспользуемся неравенством
Коши-Буняковского.

 ,
отсюда следует
,
отсюда следует
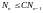 и
и
 где
где

При

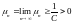 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Убедимся, что
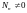 ,
тогда и
,
тогда и

Действительно
 выбрана так, что
выбрана так, что
 и, следовательно,
и, следовательно,
 и
и
 .
Из неравенства
.
Из неравенства
 и т.д.
и т.д.
 для
для
 .
.
Докажем, что чётные итерации
 сходятся в среднем к
сходятся в среднем к
некоторой
функции
 ,
а нечётные
,
а нечётные
 к
к
 .
.
Функции
 непрерывны и нормированы на единицу.
Оператор
непрерывны и нормированы на единицу.
Оператор
 переводит такие функции в последовательность
равномерно ограниченных и
равностепенно-непрерывных функций (см.
теоремы функционального анализа). Т.к.
переводит такие функции в последовательность
равномерно ограниченных и
равностепенно-непрерывных функций (см.
теоремы функционального анализа). Т.к.
 ,
то последовательность
,
то последовательность
 состоит из равномерно ограниченных и
равностепенно-непрерывных функций. По
доказанному,
состоит из равномерно ограниченных и
равностепенно-непрерывных функций. По
доказанному,
 тогда отсюда следует что последовательность
тогда отсюда следует что последовательность
 также состоит из равномерно ограниченных
и равностепенно-непрерывных функций,
что верно в отдельности и для
последовательностей
также состоит из равномерно ограниченных
и равностепенно-непрерывных функций,
что верно в отдельности и для
последовательностей
 и
и
 .
.
По
теореме Арцела существует
подпоследовательность
 последовательности
,
равномерно сходящаяся к некоторой
непрерывной функции
и из равномерной сходимости следует
сходимость
к
последовательности
,
равномерно сходящаяся к некоторой
непрерывной функции
и из равномерной сходимости следует
сходимость
к
 в среднем. Далее можно доказать, что из
этой сходимости следует , что вся
последовательность
сходится к
в среднем. Аналогично, устанавливается
сходимость в среднем последовательности
в среднем. Далее можно доказать, что из
этой сходимости следует , что вся
последовательность
сходится к
в среднем. Аналогично, устанавливается
сходимость в среднем последовательности
 к некоторой непрерывной функции
и
доказывается что из равностепенной
непрерывности и сходимости в среднем
следует её
равномерная сходимость к
рассмотреть
самостоятельно. И так
к некоторой непрерывной функции
и
доказывается что из равностепенной
непрерывности и сходимости в среднем
следует её
равномерная сходимость к
рассмотреть
самостоятельно. И так
 равномерно. Аналогично доказывается,
что
равномерно. Аналогично доказывается,
что
 также
равномерно. Совершая предельный переход
в (12.4) () по последовательности с чётными
и нечётными номерами, получим
также
равномерно. Совершая предельный переход
в (12.4) () по последовательности с чётными
и нечётными номерами, получим
 ,
,
 (11.5)
(11.8)
(12.5)
(11.5)
(11.8)
(12.5)
Откуда
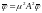 или
или

Последнее равенство возможно в двух случаях:
а)
 ,
т.е.
,
т.е.
 и
и
 является собственным значением уравнения
(12.1), а из (12.5)
является собственным значением уравнения
(12.1), а из (12.5)
 что
что
 .
.
б)
 ,
тогда
,
тогда
 ,
или
,
или
 .
.
Следовательно,
 является собственным значением уравнения
(11.1)
(11.4)
(12.1) . Из (11.5)
(11.8)
(12.5) тогда следует, что
является собственным значением уравнения
(11.1)
(11.4)
(12.1) . Из (11.5)
(11.8)
(12.5) тогда следует, что

Таким
образом, либо
 ,
тогда
,
тогда
 ,
либо
,
либо
 и тогда
и тогда
 являются собственным значением и
собственной функций уравнения (11.4)
(12.1).
являются собственным значением и
собственной функций уравнения (11.4)
(12.1).
Итак, мы доказали существование собственных значений и собственных функций и построили алгоритм их определения.
Пример. Найти собственные значения и функции уравнения
 (11.6)
(11.9)
(11.6)
(11.9)
Возьмем
 и в соответствии с (11.2)
(11.5) при n=1,2,…,n
найдём
и в соответствии с (11.2)
(11.5) при n=1,2,…,n
найдём


……………………………………………………………………
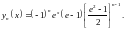
Далее
находим
 и строим нормированные
функции
и строим нормированные
функции
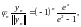 откуда следует
откуда следует

т.е.
 - является собственной функцией данного
интегрального уравнения, соответствующей
собственному значению
- является собственной функцией данного
интегрального уравнения, соответствующей
собственному значению .
.
