Вторая фундаментальная теорема Фредгольма

Теорема 7. Если есть корень уравнения ранга q, то однородное интегральное уравнение

(26)

имеет q линейно независимых решений и каждое другое решение выражается через них линейно и однородно. Эта система независимых решений определяется формулами

К №(26)

_{В формуле (10.4)} для всех i любые, при которых

Пример 7. Найти решение интегрального уравнения

!!!....

_{Дадим далее строгое доказательство второй фундаментальной теоремы Фредгольма} 21!!!...§

Рассмотрим случай , , которому в линейной алгебраической системе соответствует обра­щение в нуль определителя со всеми его первыми минорами. Тогда, как известно, становится необходимым рассмотрение мино­ров высшего порядка. Соответственно этому для случая интеграль­ного уравнения нам необходимо найти предельные выражения, к ко­торым стремятся высшие миноры определителя , когда .

В последующем мы будем употреблять вместе с Хейвудом и Фреше (Heywood — Frechet, L’Equation de Fredholm [Ловит У.В.]) обозначение

а) Определение p-го минора для . Пусть

(28) (13.2) (10.6)

и

. (29) (10.7)

Тогда p-й минор для , по определению, выражается рядом

, (30) (10.8)

который при p= 1 приводится к .

С помощью теоремы Адамара можно доказать, вполне анало­гично тому, как мы делали это раньше, следующую теорему.

Теорема 9. Бесконечный ряд для абсолютно сходится для всех значений и равномерно относительно ; , удовлетворяющих неравенствам , .

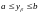
Следствие. Если два значения x с различными индексами становятся равными, например , или же два значения y: , то обращается в нуль.

Действительно, тогда в определителе, стоящем в выражении (28)(10.6) для под знаком интеграла, две строки (два столбца) становятся одинаковыми. Поэтому

,

и, следовательно,

На таком же основании, если в переменить местами два или же два с разными индексами, то переменит знак.

б) Обобщение фундаментальных соотношений Фредгольма. Разложим определитель, стоящий в под знаком интеграла, по элементам столбца

.

В первой сумме множитель , можно вынести за знак инте­грала. Тогда согласно формуле (28)(10.6) эта сумма перейдет в

.

Если мы переменим обозначения во второй сумме и вместо напишем то i-й член этой суммы примет вид

.

Перенесем теперь столбец t на место между столбцами и , на что понадобится перестановок. Тогда для i-го члена второй суммы мы получим выражение

,

которое показывает, что все члены второй суммы равны между собой. Поэтому, если мы проинтегрируем сперва по , эту сумму можно будет записать в виде

что согласно формуле (28)(10.6) приводится к

.

Таким образом, мы пришли к формуле

. (31)(10.9)

Подобным же образом, разлагая определитель, стоящий в выра­жении (28)(10.6) для под знаком интеграла, по элементам строки , мы получим формулу

. (32)(10.10)

Умножая теперь обе части формул (31)(10.9) и (32)(10.10) на 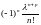и суммируя по от до , мы получаем согласно формуле (30)(10.8) следующие два соотношения, представляющие собой обобщения фундаментальных соотношений Фредгольма (10)(7.11) и (11)(7.10)

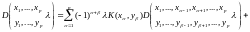
(33)(10.11)

. (34)(10.12)

Отметим аналогию с конечной системой линейных алгебраических уравнений с определителем . Если , то эта система имеет одно и только одно решение. Если все , то единственным решением является тривиальное .

Если ввести определитель являющийся пределом определителя _, то по аналогии с конечной системой линейных алгебраических уравнений можно ожидать, что имеют место аналогичные теоремы и ее следствия для интегральных уравнений Фредгольма.

в) Соотношение между и .

Соотношение (27)(10.3) между и является частным случаем следующего общего соотношения:

(35)(10.13)

Доказательство. Дифференцируя 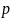раз подряд ряд

мы получаем

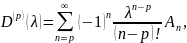
что после замены на принимает вид

Но по формуле (15)(8.2)

Если теперь вместо мы подставим и переменим затем порядок интегрирования, производя сначала интегрирование по , то получим

что согласно формуле (28)(10.6) переходит в

Помножив обе части этого равенства на и суммируя затем по от до , мы получим

Здесь суммирование можно произвести под знаком кратного интеграла. Применяя после этого формулу (30)(10.8), получаем

и формула (35)(10.13) доказана.

Применим этот результат для доказательства того, что не все миноры Фредгольма обращаются в нуль. Пусть будет корень уравнения Тогда , так как . Далее, корень имеет конечную кратность

Конечной кратность корня должна быть потому, что в противном случае мы имели бы

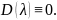
Положим в формуле (35)(10.13) и ; тогда интеграл, стоящий в левой части этой формулы, будет отличен от нуля, ибо согласно нашему предположению правая часть не равна нулю. Так как то отсюда следует, что

и, значит,

Поэтому, рассматривая последовательность

мы должны прийти к некоторому числу называемому рангом корня , такому, что

Последнее неравенство выражает собой, что существует некоторая совокупность значений принимаемых переменными 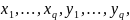при которой имеет место численное неравенство

В ходе наших рассуждений мы попутно доказали следующую теорему.

Теорема 6. Ранг корня уравнения не превосходит кратности этого корня

г) независимых решений однородного уравнения.

Пусть будет корнем уравнения с рангом , так что

но

Напишем второе обобщенное фундаментальное соотношение Фредгольма (34)(10.12) для значений , ,

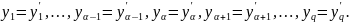
При этих значениях оно примет вид

ибо по предположению

Если мы теперь разделим обе части полученного равенства на

и положим

(36)(10.14)

то будем иметь что выражает, что функции

являются решениями однородного уравнения (26)(10.1). Эти решения непрерывны, причем по формулам (30)(10.8) и (28)(10.6)

(37)(10.15)

Далее, они линейно независимы, т.е. если найдено какое-нибудь соотношение вида

где постоянные, а , то должно быть . В самом деле, положив в этом соотношении , мы получим по формулам (37)(10.15), что

Из однородности уравнения (26)(10.1) следует, что функция

(38)(10.16)

где произвольные постоянные, также является решением уравнения (26)(10.1). Таким образом, мы уже имеем решений.

д) Доказательство полноты.

Остается показать, что каждое решение уравнения (26)(10.1) может быть представлено виде (38)(10.16).

Если есть какое-нибудь решение уравнения (26)(10.1):

то отсюда следует, что для любой непрерывной функции выполняется тождество

Вычитая почленно второе равенство из первого, получаем

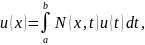(39)(10.17)

где

Положим теперь в формуле (33)(10.11) , , .

Замечая, что перемена местами двух или двух с разными индексами изменяет знак при , мы получим

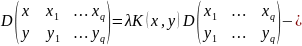
Если мы выберем для 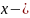ов и значения

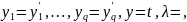разделим обе части этой формулы на

и введем обозначение

(40)(10.18)

то получим:

(41)(10.19)

Так как правая часть этого равенства есть не что иное, как , то мы можем переписать уравнение (39)(10.17) следующим образом:

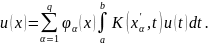
Это показывает, что может быть написано в форме (38)(10.16), если придать постоянным значения

Таким образом, мы получили вторую фундаментальную теорему Фредгольма.

!!! §11. Собственные значения и собственные функции