
- •010400.62 «Прикладная математика и информатика»
- •Введение
- •§1. Классификация интегральных уравнений
- •§2. Решение интегральных уравнений Фредгольма методом последовательных приближений
- •§3. Уравнения с вырожденными ядрами
- •§4. Решение интегральных уравнений Фредгольма с помощью ряда Неймана
- •§5. Итерированные ядра и резольвента интегральных уравнений Фредгольма
- •§6. Решение линейных интегральных уравнений Фредгольма второго рода методом последовательных подстановок
- •§7. Уравнение Фредгольма как предел системы конечного числа линейных алгебраических уравнений. Фундаментальные соотношения Фредгольма
- •§8. Доказательство сходимости рядов Фредгольма
- •§9. Решение интегрального уравнения, данное Фредгольмом при . Первая фундаментальная теорема Фредгольма
- •20…§10. Решение однородных интегральных уравнений. Вторая фундаментальная теорема Фредгольма
- •Вторая фундаментальная теорема Фредгольма
- •И их вычисление
- •§12. Вычисление собственных значений и собственных функций по методу Келлога
- •§13. Сопряжённые однородные интегральные уравнения
- •§23. Перед тем, как перейти к исследованию неоднородного интегрального уравнения при , рассмотрим однородное интегральное уравнение
- •§15. Теорема Адамара
- •§16. Обзор других методов решения. Приближённые методы решения
- •§16. Задачи для самостоятельного решения
- •Примерный вариант тест-контрольной работы
- •Литература
- •Оглавление
- •Тест-контрольная по интегральным уравнениям Вольтерра
- •1 Вариант
- •9.Записать решение уравнения, если резольвента ядра известна
- •Вариант
- •Вариант
- •Вариант
- •Вариант теста по интегральным уравнениям Вольтерра
- •Ответы к тестам по интегральным уравнениям Вольтерра
- •Блок1. Интегральные уравнения Вольтерра
§6. Решение линейных интегральных уравнений Фредгольма второго рода методом последовательных подстановок
Рассмотрим уравнение Фредгольма второго рода
 ,
(6.1)
,
(6.1)
где
функция
 вещественна и непрерывна в прямоугольнике
вещественна и непрерывна в прямоугольнике
 функция
функция
 вещественна и непрерывна в интервале
вещественна и непрерывна в интервале

 – постоянное число.
– постоянное число.
Нетрудно
увидеть, что если существует непрерывное
решение
уравнения (6.1) и функция
 непрерывна, то тогда и функция
непрерывна, то тогда и функция
 должна быть непрерывной.
должна быть непрерывной.
Подставляя
в правую часть уравнения (6.1) вместо
функции
 ее выражение из того же уравнения (6.1),
находим
ее выражение из того же уравнения (6.1),
находим

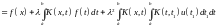 .
.
Снова
подставляя сюда вместо
 его значение из уравнения (6.1), получаем
его значение из уравнения (6.1), получаем
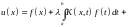


 .
.
После
 –й
подстановки мы будем иметь:
–й
подстановки мы будем иметь:


 (6.2)
(6.2)
где
 .
.
Это приводит нас к рассмотрению следующего бесконечного ряда:


 (6.3)
(6.3)
В
силу непрерывности функций входящих в
уравнение (6.1), ряд (6.3), если он равномерно
сходится в
 ,
представляет в этом интервале некоторую
непрерывную функцию.
,
представляет в этом интервале некоторую
непрерывную функцию.
Так
как
и
непрерывны соответственно в
 и
,то
и
,то
 в
,
в
,
 в
.
в
.
Рассмотрим
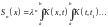
 .
.
Согласно написанным выше неравенствам, имеем
 .
.
Ряд с таким общим членом сходится, лишь если
 .
.
Таким образом, мы видим, что ряд (6.3) сходится абсолютно и равномерно для всех , удовлетворяющих неравенству
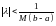 .
.
Если
уравнение (6.1) имеет непрерывное решение,
то оно должно удовлетворять формуле
(6.2). Но так как по предположению
непрерывно в
,
то его абсолютное значение имеет в этом
интервале некоторый максимум:  Тогда
Тогда
 .
.
Если теперь будет выполняться неравенство ,
то
 .
.
Таким образом, мы видим, что функция , удовлетворяющая формуле (6.2) при любом , разлагается в ряд (6.3).
Можно
убедиться путем непосредственной
подстановки, что функция
,
представляющая сумму ряда (6.3), удовлетворяет
уравнению (6.1). К этому же результату
приводит и другой путь: обозначим сумму
ряда (6.3) через
,
помножим обе части полученного равенства
на
 и проинтегрируем ряд почленно, что мы
вправе сделать. Тогда получим
и проинтегрируем ряд почленно, что мы
вправе сделать. Тогда получим

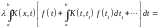
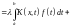

Итак, мы получили следующую теорему.
Теорема 2. Если в уравнении
функция
вещественна и непрерывна в прямоугольнике
и
,
функция
вещественна и непрерывна в интервале
,
– постоянное число и
 ,
,
то уравнение (6.1) имеет одно и только одно решение выражающееся абсолютно и равномерно сходящимся рядом (6.3).
Уравнение (6.1) имеет непрерывные решения, даже если условие
не выполняется. Правильность этого утверждения можно иллюстрировать следующим примером.
Пример 4. Уравнение

имеет
непрерывное решение
 ,
тогда как
,
тогда как
 .
.
§7. Уравнение Фредгольма как предел системы конечного числа линейных алгебраических уравнений. Фундаментальные соотношения Фредгольма
Решение уравнения
 (7.1)
(7.1)
данное в предыдущем параграфе, обладает тем недостатком, что оно имеет силу для ограниченных значений параметра . Желательно же иметь, если это возможно, такое решение, которое было бы справедливо при всех . Такое решение было дано Фредгольмом в форме

где числитель и знаменатель – степенные ряды, сходящиеся при всех значениях .
Система линейных алгебраических уравнений, заменяющих интегральное уравнение. Прежде чем излагать полно и строго полученные Фредгольмом результаты, мы наметим в общих чертах те основания, которые привели к их открытию.
Разделим
интервал
 на
на
 равных частей и
обозначим точки деления через
равных частей и
обозначим точки деления через
 Тогда
Тогда
 . (7.2)
. (7.2)
Если мы заменим определенный интеграл в уравнении (7.1) суммой, соответствующей точкам деления (7.2), пределом которой он является, то получим приближенное уравнение
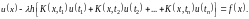 Так
как это уравнение имеет место для всех
значений
Так
как это уравнение имеет место для всех
значений
 ,
то оно должно
удовлетворяться, в частности, и для
,
то оно должно
удовлетворяться, в частности, и для
 Тем самым мы получаем
следующую систему n
линейных уравнений относительно
неизвестных
Тем самым мы получаем
следующую систему n
линейных уравнений относительно
неизвестных

 (7.3)
(7.3)
Разрешив
эту систему относительно
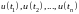 ,
мы сможем нанести найденные значения
как ординаты и провести через вершины
этих ординат интерполяционную кривую
,
мы сможем нанести найденные значения
как ординаты и провести через вершины
этих ординат интерполяционную кривую
 смотри чертёж 2
смотри чертёж 2
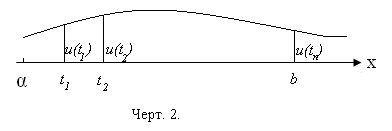 Мы
вправе ожидать, что эта кривая будет
приближенно представлять действительное
решение.
Мы
вправе ожидать, что эта кривая будет
приближенно представлять действительное
решение.
Будем
писать для сокращения

и
обозначим через
 определитель, составленный из
коэффициентов, стоящих при неизвестных
определитель, составленный из
коэффициентов, стоящих при неизвестных
 в написанной выше системе уравнений
(7.3)
в написанной выше системе уравнений
(7.3)

Если
мы обозначим через
 алгебраическое дополнение элемента,
находящегося на пересечении
алгебраическое дополнение элемента,
находящегося на пересечении
 -й
строки и
-й
строки и
 -го
столбца определителя
-го
столбца определителя
![]() , то, разрешая систему уравнений (7.3)
относительно
, то, разрешая систему уравнений (7.3)
относительно
 мы
получим по формулам Крамера
мы
получим по формулам Крамера
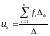
 (7.4)
(7.4)
в
предположении, что
 .
.
Предел определителя . Развертывая по степеням
 ,
получаем
,
получаем

Если теперь мы будем безгранично увеличивать , то каждый член этого ряда будет стремится к определенному пределу. Таким образом, по крайней мере формально, мы получим

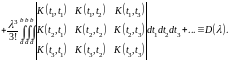 (7.5)
(7.5)
 называют
определителем
Фредгольма
ядра
называют
определителем
Фредгольма
ядра
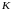 .
.
Предел
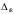 .
Определитель
.
Определитель
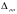 развертывается по степеням
совершенно аналогично
тому, как это имеет место для
развертывается по степеням
совершенно аналогично
тому, как это имеет место для

где
знак
 означает, что сумма
не распространяется на члены с индексом
означает, что сумма
не распространяется на члены с индексом
 .
Переходя к пределу, получаем
.
Переходя к пределу, получаем
 (7.6)
(7.6)
Далее согласно правилам разложения определителей
 Положим
Положим
 .
Если при бесконечном увеличении
мы будем изменять
.
Если при бесконечном увеличении
мы будем изменять
 так, чтобы
так, чтобы
 ,
то, по крайней мере формально, получим
,
то, по крайней мере формально, получим


 .(6.7)
(6.8)
.(6.7)
(6.8)
Это выражение называют первым минором Фредгольма.
Предел
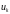 .
Выражение (7.4) можно переписать в форме
.
Выражение (7.4) можно переписать в форме
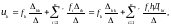
что
в пределе, при
 ,
переходит в
,
переходит в
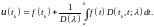
Но
 есть любая точка деления. Поэтому мы
можем заменить
на
есть любая точка деления. Поэтому мы
можем заменить
на
 и написать
и написать
 (7.9)
(7.9)
Путь,
которым мы получили этот результат, не
является строгим математическим путем.
Тем не менее представляется весьма
вероятным, что выражение (7.9) для
 действительно есть решение уравнения
(7.1). Ниже будет показано, что это на самом
деле так.
действительно есть решение уравнения
(7.1). Ниже будет показано, что это на самом
деле так.
Фундаментальные соотношения Фредгольма
Выведем теперь два соотношения, которые нам будут нужны дальше для получения решения интегрального уравнения (7.1).
Напомним одну из фундаментальных теорем теории определителей, которая гласит, что сумма произведений элементов некоторого столбца на алгебраические дополнения соответствующих элементов другого столбца равна нулю. Эта теорема в применении к определителю дает:

где
знак
 означает, что сумма не распространяется
на значения
означает, что сумма не распространяется
на значения
 .
Применяя соотношение
.
Применяя соотношение
 ,
находим:
,
находим:

Разделим
обе части этого равенства на
 ,
что мы можем делать, раз
,
что мы можем делать, раз
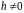 .
При
полученное после деления на
уравнение перейдет согласно формулам
(7.6) и (7.7) в
.
При
полученное после деления на
уравнение перейдет согласно формулам
(7.6) и (7.7) в

Последнее
уравнение имеет место для любых двух
значений
 ,
лежащих в интервале
,
лежащих в интервале
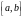 .
Поэтому мы можем положить
.
Поэтому мы можем положить
 ,
,
 и написать:
и написать:
 (7.10)
(7.10)
Это есть второе фундаментальное соотношение Фредгольма.
Применим теорему: сумма произведений элементов некоторой строки на алгебраические дополнения соответствующих элементов любой другой строки равна нулю. Эта теорема в применении к определителю дает

Поступая как выше, находим:
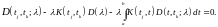
Это
уравнение имеет место для любых двух
значений
 лежащих в промежутке
. Поэтому полагаем
лежащих в промежутке
. Поэтому полагаем
 и пишем
и пишем
 (7.11)
(7.11)
Это есть первое фундаментальное соотношение Фредгольма.
Эти фундаментальные соотношения нетрудно получить из уравнений резольвенты (5.7) и (5.8), если положив

умножить
каждое
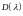 при условии что
при условии что

