
- •010400.62 «Прикладная математика и информатика»
- •Введение
- •§1. Классификация интегральных уравнений
- •§2. Решение интегральных уравнений Фредгольма методом последовательных приближений
- •§3. Уравнения с вырожденными ядрами
- •§4. Решение интегральных уравнений Фредгольма с помощью ряда Неймана
- •§5. Итерированные ядра и резольвента интегральных уравнений Фредгольма
- •§6. Решение линейных интегральных уравнений Фредгольма второго рода методом последовательных подстановок
- •§7. Уравнение Фредгольма как предел системы конечного числа линейных алгебраических уравнений. Фундаментальные соотношения Фредгольма
- •§8. Доказательство сходимости рядов Фредгольма
- •§9. Решение интегрального уравнения, данное Фредгольмом при . Первая фундаментальная теорема Фредгольма
- •20…§10. Решение однородных интегральных уравнений. Вторая фундаментальная теорема Фредгольма
- •Вторая фундаментальная теорема Фредгольма
- •И их вычисление
- •§12. Вычисление собственных значений и собственных функций по методу Келлога
- •§13. Сопряжённые однородные интегральные уравнения
- •§23. Перед тем, как перейти к исследованию неоднородного интегрального уравнения при , рассмотрим однородное интегральное уравнение
- •§15. Теорема Адамара
- •§16. Обзор других методов решения. Приближённые методы решения
- •§16. Задачи для самостоятельного решения
- •Примерный вариант тест-контрольной работы
- •Литература
- •Оглавление
- •Тест-контрольная по интегральным уравнениям Вольтерра
- •1 Вариант
- •9.Записать решение уравнения, если резольвента ядра известна
- •Вариант
- •Вариант
- •Вариант
- •Вариант теста по интегральным уравнениям Вольтерра
- •Ответы к тестам по интегральным уравнениям Вольтерра
- •Блок1. Интегральные уравнения Вольтерра
§2. Решение интегральных уравнений Фредгольма методом последовательных приближений
Рассмотрим линейное уравнение второго рода
 .
(2.1)
.
(2.1)
Теорема 1.
Уравнение (2.1), если свободная функция и ядро
и ядро
 - непрерывные функции при
- непрерывные функции при
 ,
имеет единственное непрерывное решение
при достаточно малом значении параметра
.
Это решение может быть найдено методом
последовательных приближений.
,
имеет единственное непрерывное решение
при достаточно малом значении параметра
.
Это решение может быть найдено методом
последовательных приближений.
Доказательство.
Примем за начальное приближение свободную
функцию
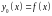 .
.
Выпишем рекуррентную формулу последовательных приближений по методу Пикара
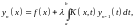
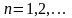 (2.2)
(2.2)
В
соответствии с условием теоремы имеем
ограничения
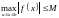 и
и
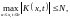 используя которые оценим последовательные
приближения (2.2) по модулю
используя которые оценим последовательные
приближения (2.2) по модулю





……………………………………………………………………………
……………………………………………………………………………

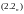
……………………………………………………………………………
Тогда для сходимости метода необходимо выполнение условия
 (2.3)
(2.3)
Так
как при
 получим ряд составленный из членов
геометрической прогрессии который
сходится при условии (2.3), то
получим ряд составленный из членов
геометрической прогрессии который
сходится при условии (2.3), то
 (2.4)
(2.4)
Методом от противного можно доказать единственность полученного решения, аналогично как и для уравнений Вольтерра.
Пример 1. Решить интегральное уравнение применив метод последовательных приближений

Решение. Приняв за начальное приближение к решению свободную функцию, последовательно найдём



 ……………………………………………………………………………
,
……………………………………………………………………………
,

……………………………………………………………………,

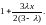
Сделать проверку, подставив полученное решение в исходное уравнение.
§3. Уравнения с вырожденными ядрами
Рассмотрим интегральные уравнения, ядра которых имеют вид

Интегральное уравнение Фредгольма

можно будет теперь написать в виде

 (3.1)
(3.1)
или, если положить
 ,
(3.2)
,
(3.2)
в виде
 (3.3)
(3.3)
Подставляя
в формулу (3.2) значение функции
 из равенства (3.3), мы получим для определения
постоянных
из равенства (3.3), мы получим для определения
постоянных

 уравнений
уравнений

 (3.4)
(3.4)
которые после введения обозначений

примут вид
 (3.5)
(3.5)
Уравнения
(3.5) представляют собой систему
неоднородных линейных алгебраических
уравнений относительно неизвестных
 с определителем
с определителем
 .
.
Из теории линейных алгебраических уравнений мы получаем сразу следующие результаты:
а) Если
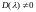 ,
то уравнения (3.4) допускают одну и только
одну систему решений
,
определяемых по формулам Крамера.
Поэтому уравнение (3.1) имеет одно и только
одно решение, представляющееся формулой
(3.3).
,
то уравнения (3.4) допускают одну и только
одну систему решений
,
определяемых по формулам Крамера.
Поэтому уравнение (3.1) имеет одно и только
одно решение, представляющееся формулой
(3.3).
б) Если
 для некоторого
для некоторого
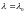 (что имеет место для
значений
(что имеет место для
значений
 ,
вещественных или же комплексных) и
первым минором определителя
,
вещественных или же комплексных) и
первым минором определителя
 ,
не обращающимся в нуль при
,
является какой-либо минор
,
не обращающимся в нуль при
,
является какой-либо минор
 -го
порядка (т.е. определитель
-го
порядка (т.е. определитель
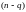 -го
порядка), то общее решение однородной
системы (3.4) при
-го
порядка), то общее решение однородной
системы (3.4) при будет иметь вид
будет иметь вид
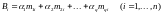 ,
,
где
 -
произвольные постоянные.
-
произвольные постоянные.
Если мы вставим найденные таким образом значения в (3.3), то получим:
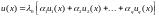 ,
,
где функции

линейно независимы.
Таким образом, мы видим, что при выполнении некоторых условий однородное интегральное уравнение с параметром имеет линейно независимых решений.
Сопряженное уравнение
 (3.6)
(3.6)
получится
из уравнения (3.1) после перемены местами
всех функций
 и
и
 .
Общий член определителя уравнения (3.1)
был:
.
Общий член определителя уравнения (3.1)
был:
.
Поэтому общий член определителя для сопряженного уравнения будет:
 .
.
Эти два определителя равны друг другу, так как один получается из другого путем перестановки столбцов и строк. Поэтому уравнение (3.1) и сопряженное уравнение (3.6) имеют одинаковые собственные значения с одинаковыми рангами.
Из
общей теории мы знаем, что если
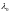 есть корень уравнения
ранга
,
то для того, чтобы неоднородное уравнение
(3.1) могло иметь решение, необходимо,
чтобы выполнялись условия
есть корень уравнения
ранга
,
то для того, чтобы неоднородное уравнение
(3.1) могло иметь решение, необходимо,
чтобы выполнялись условия
 .
.
Пример 2. Решить интегральное уравнение применив метод вырожденных ядер
Решение. Из
под интеграла вынесем x
и положим

тогда
данное уравнение перепишется
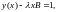 откуда
найдём
откуда
найдём
 и, затем, подставив полученное выражение
для
и, затем, подставив полученное выражение
для
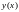 в заданное уравнение
в заданное уравнение

и вычислив интеграл,
найдём
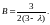
И, затем, подставив это значение В в выражение для
найдём
решение интегрального уравнения

