
- •010400.62 «Прикладная математика и информатика»
- •Введение
- •§1. Классификация интегральных уравнений
- •§2. Решение интегральных уравнений Фредгольма методом последовательных приближений
- •§3. Уравнения с вырожденными ядрами
- •§4. Решение интегральных уравнений Фредгольма с помощью ряда Неймана
- •§5. Итерированные ядра и резольвента интегральных уравнений Фредгольма
- •§6. Решение линейных интегральных уравнений Фредгольма второго рода методом последовательных подстановок
- •§7. Уравнение Фредгольма как предел системы конечного числа линейных алгебраических уравнений. Фундаментальные соотношения Фредгольма
- •§8. Доказательство сходимости рядов Фредгольма
- •§9. Решение интегрального уравнения, данное Фредгольмом при . Первая фундаментальная теорема Фредгольма
- •20…§10. Решение однородных интегральных уравнений. Вторая фундаментальная теорема Фредгольма
- •Вторая фундаментальная теорема Фредгольма
- •И их вычисление
- •§12. Вычисление собственных значений и собственных функций по методу Келлога
- •§13. Сопряжённые однородные интегральные уравнения
- •§23. Перед тем, как перейти к исследованию неоднородного интегрального уравнения при , рассмотрим однородное интегральное уравнение
- •§15. Теорема Адамара
- •§16. Обзор других методов решения. Приближённые методы решения
- •§16. Задачи для самостоятельного решения
- •Примерный вариант тест-контрольной работы
- •Литература
- •Оглавление
- •Тест-контрольная по интегральным уравнениям Вольтерра
- •1 Вариант
- •9.Записать решение уравнения, если резольвента ядра известна
- •Вариант
- •Вариант
- •Вариант
- •Вариант теста по интегральным уравнениям Вольтерра
- •Ответы к тестам по интегральным уравнениям Вольтерра
- •Блок1. Интегральные уравнения Вольтерра
§16. Обзор других методов решения. Приближённые методы решения
§16. Задачи для самостоятельного решения
I. Проверить являются ли данные функции решением интегральных уравнений:
64.
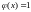 ,
,
 .
Ответ: да.
.
Ответ: да.
65.
 ,
,
 Ответ: да.
Ответ: да.
66.
 ,
,
 Ответ: да.
Ответ: да.
67.
 ,
,

 Ответ:
да.
Ответ:
да.
68.
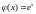 ,
,
 Ответ: нет.
Ответ: нет.
69.
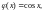
 Ответ: нет.
Ответ: нет.
70.

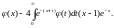 Ответ: да.
Ответ: да.
71.



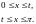 Ответ:
да.
Ответ:
да.
72.
 где
где
 произвольная
постоянная,
произвольная
постоянная,
 Ответ:
да.
Ответ:
да.
II.Решить интегральные уравнения Фредгольма методом последовательных приближений:
Методом последовательных приближений решить следу ющие интегральные уравнения:
319.

320.
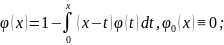 321.
321.

322.
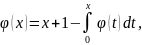
a)
 б)
б)
Метод последовательных приближений
323.
a)
б)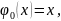 в)
в)
324.

325.

a)
б)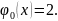
326.

a)
 б)
б)
327.

Метод последовательных приближений решить уравнение
!!!...335.

K(x,t)=
336.

K(x,t)=
III.
Решить
интегральные уравнения Фредгольма
методом для вырожденных ядер если
 ,
где не даны ответы, сделать проверку:
,
где не даны ответы, сделать проверку:
11.
 12.
12.
13. 14.
14.
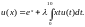
15.
 16.
16.
17. 25.
25.

26. 27.
27.
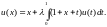 28.
28.
 29.
29.
111.
 .
Ответ:
.
Ответ:

112.
 .
Ответ:
.
Ответ:

113.
 .
Ответ:
.
Ответ:
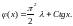
114.
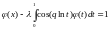 .
Ответ:
.
Ответ:
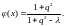
115.
 .
.
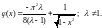
118.
 .
Ответ:
.
Ответ: 
119.
 .
Ответ:
.
Ответ:

120.
 .
Ответ:
.
Ответ: 
121.

Ответ:

122.
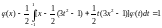 .
.
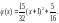
!!!.... IV. Найти итерированные ядра указанных ниже ядер при данных a и b.
92. K(x,t)=x-t; a=-1, b=1.
93.
K(x,t)=sin(x-t);
a=0, b= , (n=2,3)
, (n=2,3)
94. K(x,t)=(x-t)2; a=-1, b=1, (n=2,3)
95. K(x,t)=x+sin(t); a=-π, b=π.
96. K(x,t)=xet; a=0, b=1.
97. K(x,t)=excos(t); a=0, b=π.
В следующих задачах найти K2(x,t):
98. K(x,t)=e|x-t|; a=0, b=1.
99. K(x,t)=e|x|+t; a=-1, b=1.
IV. Решить интегральные уравнения Фредгольма вычислив итерированные ядра и резольвенту:
!!!...... С помощью резольвенты решить следующие интегральные уравнения:
87.

88.
89.

90.
 x-t
x-t x
x
91.
 2
2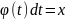
V. Пользуясь определителями Фредгольма, найти резольвенты следующих ядер:
77.

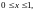

Ответ: 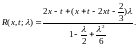
78.

Ответ: 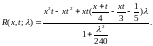
79.
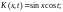



80.



Ответ: 
!!!.....Используя рекуррентные соотношения (8) и (9), найти резольвенты следующих ядер:
81.
K(x,t)=x+t+1;
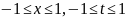
82.
K(x,t)=1+3xt;

83. K(x,t)=4xt-x2;
84. K(x,t)=ex-t;
85.
K(x,t)=sin(x+t);

86. K(x,t)=x-sh(t);
Построить резольвенты для следующих ядер:
100. K(x,t)=ex+t; a=0, b=1.
101. K(x,t)=sin(x)cos(t); a=0, b= .
102. K(x,t)=xet; a=-1, b=1.
103. K(x,t)=(1+x)(1-t); a=-1, b=0.
104. K(x,t)=x2t2; a=-1, b=1.
105. K(x,t)=xt; a=-1, b=1.
VI. Вычислить и для уравнения Фредгольма со следующими ядрами и пределами интегрирования:
1.

Отв.

2.

Отв.
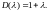
3.

Отв.

4.

Отв.

5.

Отв.

6.

Отв.

7.

Отв.
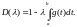
8.
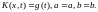
Отв.
9.

Отв.

10.

Отв.

V
II.
Решить
интегральные уравнения Фредгольма
вычислив
и
V III. Решить следующие однородные интегральные уравнения:
18.

22.

19.

23.

20.

24.

21.

IХ. Найти характеристические числа и собственные функции для следующих однородных интегральных уравнений с вырожденным ядром:
123. .
Ответ:
.
Ответ:
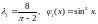
124.
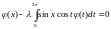 .
Ответ: нет.
.
Ответ: нет.
125.
 .
Ответ:
.
Ответ:
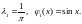
126.
 .
Ответ:
.
Ответ:

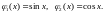
127.
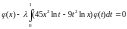 .
Ответ: действительных
нет.
.
Ответ: действительных
нет.
128.
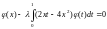 ,
Ответ:
,
Ответ:
 129.
129.
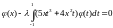 .
Ответ:
.
Ответ:

130.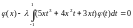 .
Ответ:
.
Ответ:

131.
 .
Ответ:
.
Ответ:

132.
 .
Ответ: нет.
.
Ответ: нет.
133.
 Ответ: действительных
нет.
Ответ: действительных
нет.
По методу Келлога найти наименьшие характеристические числа следующих ядер:
347.
K(x,t) = xt;

348. K(x,t
)=

349.
K(x,t) =
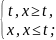
350.
K(x,t) =
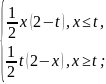
Х. Решить неоднородные интегральные уравнения:
11.
15.
12.
16.
13.
17.

14. 165.
166.
 ,
,
K(x,t)=
167.
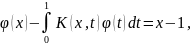
K(x,t)=
168.

K(x,t)=
169.

K(x,t)=
170.

K(x,t)=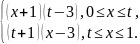
171.

K(x,t)=
172.

K(x,t)=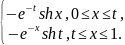
173.

K(x,t)=
174.

Исследовать на разрешимость при различных значениях параметра следующие интегральные уравнения:
175.
 .
.
176.
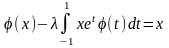 .
.
177.
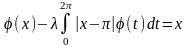 .
.
178.
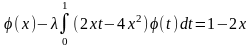 .
.
179.
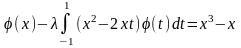 .
.
180.
 .
.
181.
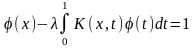 ,
где
,
где
K(x,
t) =

182.
 .
.
183.
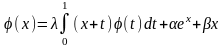 .
.
184. .
.
