6. Циліндричні та конічні поверхні. Поверхні обертання.

О. Поверх. наз. циліндричною, якщо вона разом з кожною своєю т. 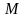містить і пряму, яка проход. через т. паралел. до деякого фіксован. . Ці прямі наз прямолінійними твірними поверхні. Циліндр. пов. можна задати вект. 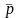її прямол твірних і лінією , вздовж якої рух твірні. Цю лінію наз напрямною лінією.

Вив р-ня. Нехай у пр-рі заф. АСК, напрямна лінія визн. р-ням 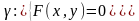, а напрямок твірних визнач 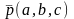, т. . позначимо тт. перетину прямої з лінією через N(x₀;y₀;Z₀), але тоді 1) Nє

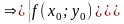
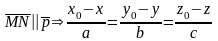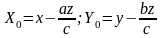
2) Виразимо з цієї пропорції хо та у0, врахувавши, що z₀=0. Пр. 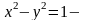гіпербол циліндр 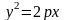-парбол. Цилін.

О. Пов наз конічною з вершин в т. 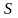, якщо разом з кожною своєю т. 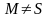вона містить і всю пряму 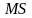. Ці прямі наз прямолінійними твірними конічної поверхні.

Конічну пов. можна задати вершиною і напрямн. Лін. , розглянувши об’єднання всіх прямих, які сполучають т. з т. лінії 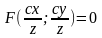–р-ня конічн пов за викл вершини Пр.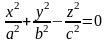 –конус

О: Поверхнею обертання з віссю обертання l наз пов, яка разом з кожною своєю т м містить і все коло, яке описує т м при обертанні навколо вісі l. О. пов. обертання наз. Пов.,яка разом з кожною своєю т. містить і все коло, яке одержане при обертанні цієї т. навколо фіксованої прямої. Ця пряма наз віссю обертання. Пов. оберт задають віссю оберт і лінією яка обертається навколо цієї осі. Якщо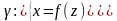 а вісь оберт 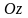то 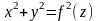– р-ня пов. обертання.

7. Пов ІІ порядку. Еліпсоїди, гіперболоїди, параболоїди. Класиф. О:Еліпсоїдом наз. Пов-ня яка у деяк. ДСК визн. р-ням. . Встивості: 1) Р-ня не змін. При зміні знака біля кожної із змін. Отже корд. площини є площинами симетрії, корд. вісі –осями симетрії, поч..коорд-центр симетрії. 2) З р-ня слідує, що 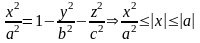, аналог. .

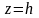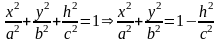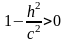3) Для дослідження форми еліпсоїда скористаємося методом перерізу, який полягає в тому, що досліджується перерізи поверхні повними сукупностями площин і на основі інформації про одержані лінії робляться висновки про поверхні. Розглянемо перерізи еліпсоїда площинами, // до координатних площин. .В перетині одерж. Лінію , а). -еліпс; б) 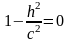-пара уяв. Пр. що перет. В дійсній точ. в) 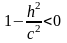- площини еліпсоїд не перетинають.Розрізняють2 типи гіперболоїдів:

О: Однопорожнинним гіперболоїдом наз. Пов-ня. Р-ня якої в деяк. ДСК має виг.

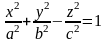
О: Двопорожнинним гіперболоїдом наз. Пов-ня, р-ня якої в деяк. ДСК має вигляд 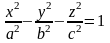. Розрізняють 2 типи параболоїдів:

О: Еліптичним параболоїдом наз. Пов-ня, яка в деяк. ДСК задається р-ням .

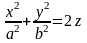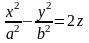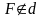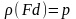О: Гіперболічним параболоїдом наз пов-ня, яка у деяк. ДСК зад. р-ням . О: Параболою наз. гмт площини, рівновіддалених від зад. пр. d і т.F, .F-фокус, d-директриса. -фокальний параметр. -канон. р-ня параб.