
- •1.Пряма на площині.
- •2. Лінії іі порядку.
- •3 Скалярний, век, міш добутки векторів.
- •2) Дистрибутивність. Дов.
- •4.Площина в просторі.
- •5. Пряма в просторі. Способи задання:
- •6. Циліндричні та конічні поверхні. Поверхні обертання.
- •8. Група рухів площини. Задання рухів.
- •9. Група перетворень подібності. Гомотетія.
- •10. Група афінних перетворень. Задання афінних перетворень.
- •11. Проективний простір. Принцип двоїстості. Т. Дезарга
- •12. Група проективних перетворень площини. Аналітичний запис
- •13. Система акс Вейля, повнота і несуперечливість.
- •14. Акс. І площина Лобачевского. Наслідки.
- •15. Многокутники. Площа мн-ка .Th існування та єдиність
- •16. Геометричні побудови на пл. Система постулатів побудов.
- •17. Топологічні простори. Гомеоморфізми. Ейлерова х-ка
- •18. Зображення плоских і простр фігур у парал проекц Теор Польке
- •19. Лінії в евкл просторі кривизна та скрут лінії Френе
- •20. Поверхні в евкл прост дот площина і нормаль до поверх
1.Пряма на площині.
Нехай
на пл. зафікс. АСК(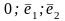 ).Способи
задання пр.:
).Способи
задання пр.:
І.т.
і напрямний вектор: розглянемо пряму,
яка проходить через т. М(х0;у0),
паралельно до р(а;в). Канонічне. р-ня:
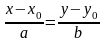 .Параметричне.
р-ня:
.Параметричне.
р-ня:
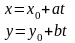 .
.
ІІ.
Дві точ. Парам.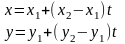 .
Канон.
.
Канон.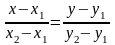 .
.
ІІІ.Точ.
і кутовий коеф.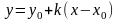 .
.
Розглян.
Р-ня
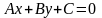 (1)
(1)
Теорема. Будь-яка пр. є лінією І порядку і навпаки, кожна лін. І пор. – пряма.
Дов.1)
Розгл. пр
 ,
доведемо, що
-лін.
І пор. Задамо на пл.. АСК і склад. р-ня
пр.
за
напр. век.
,
доведемо, що
-лін.
І пор. Задамо на пл.. АСК і склад. р-ня
пр.
за
напр. век.
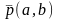 і
т.
і
т.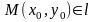
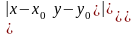 -р-ня
І пор. 2) Нех.
-р-ня
І пор. 2) Нех.
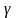 -лін
І пор, тт. її р-ня в деяк. ДСК має вид (1).
Нех.
-лін
І пор, тт. її р-ня в деяк. ДСК має вид (1).
Нех.
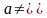 0.
тоді:
0.
тоді:
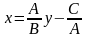 .
З точністю до позначень маємо р-ня
прямої з кутовим коефіцієнтом k=-
.
З точністю до позначень маємо р-ня
прямої з кутовим коефіцієнтом k=-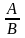 ,
яка проходить через точку
,
яка проходить через точку
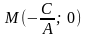 . Отже,
-
пряма. Доведено.
. Отже,
-
пряма. Доведено.
Нех
зад.АСК і пр..
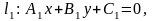
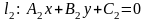 .Визначимо
взаємне розміщення прямих.
.Визначимо
взаємне розміщення прямих.
1)
прямі перетинаються:
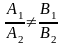
2)
прямі збігаються
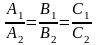
3)
прямі паралельні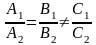
МЕТРИЧНІ ЗАДАЧІ:
1)
знаходження відстані від точки до
прямої
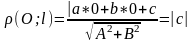
2)
Кут між 2 прямими: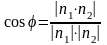
2. Лінії іі порядку.
О:
Еліпсом
наз.
гмт
площини, сума відстаней від яких до 2-х
даних точ.
 є
величина стала і більша ніж
є
величина стала і більша ніж
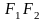 .
.
-фокуси еліпса; -фокальна відстань; відрізки що спол. Точки еліпса з фокусами – фокальні радіуси. Нех. т. М-дов точ. еліпса.F1F2=2c, MF1+MF2=2a. F1(-c;0); F2(c;0); т.М(x;y).
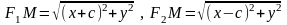
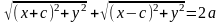
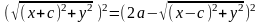
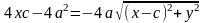
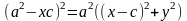 ;
;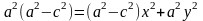
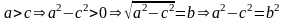
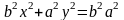 /:
/: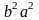
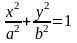 -канон.
р-ня еліпса
-канон.
р-ня еліпса
Властивості
1)
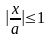 ,
,
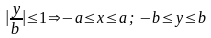 ,
,
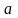 -
велика
піввісь еліпса,
-
велика
піввісь еліпса,
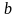 -мала.
Всі точки еліпса містяться в прямокут.
зі стор.
-мала.
Всі точки еліпса містяться в прямокут.
зі стор.
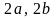 ,
тт. еліпс-фігура обмежена.
,
тт. еліпс-фігура обмежена.
2)еліпс симетричний відносно осей корд.
3)
розглянемо величину
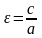 .
Зрозуміло, що
.
Зрозуміло, що
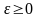 ,
,
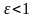 .
– ексцентриситет еліпса.
.
– ексцентриситет еліпса.
4)
Прямі, які мають рівняння х=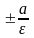 наз.
Директрисами еліпса.
наз.
Директрисами еліпса.
О: Гіперболою наз. Множ. Всіх точок площ, для кожної з яких модуль різниці відстаней до 2 фіксованих точок площини, що наз. Фокусами, є стале додатне число 2а, яке менше за відстань 2с між фокусами.
Канонічне
рівняння
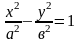 .
.
О: Праболою наз ГМТ площини, які рівновіддалені від заданої точки F та прямої d, при чому Fне належить d. Точка F – фокус, d – директриса. Рівняння у2=2рх – канонічне.
1) Рівняння є парним за змінною у, отже, парабола симетрична відносно осі ОХ, тобто має вісь симетрії.
2) х>=парабола цілком міститься у правій півплощині відносно ОУ.
3) парабола – лінія обмежена. 4) Т(0;0) – вершина параболи, крайня зліва.
3 Скалярний, век, міш добутки векторів.
О: Скалярним доб. 2-х векторів наз. число, що = добутку довжин цих век. на косинус кута між ними.
Зафікс.
У просторі ортонормований базис
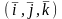 ,
,
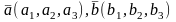 .
.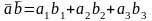
Властивості:
1.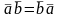 ;2.
;2.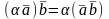 ;3.
;3.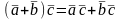 ;4.
;4.
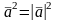 ;5.
;5.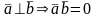
О:
Нех.
в ортонорм. просторі
дано
2 век.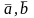 .
.
Век.
Доб.
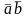 наз.
Такий вектор
наз.
Такий вектор
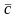 ,
який задов умовам:1)
,
який задов умовам:1)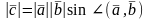 ;
;
2)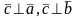 ;3)
;3)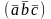 -має
орієнтацію що і базис простору.
-має
орієнтацію що і базис простору.
Властивості:
1).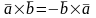 (антикомутативність);Дов.
-ортонорм.
базис;
,
тоді
(антикомутативність);Дов.
-ортонорм.
базис;
,
тоді
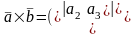 Аналогічно
Аналогічно
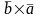 .
.
