
- •9 Клас Пояснювальна записка
- •Зміст програми
- •Література
- •Методичні рекомендації, підбір задач для занять факультативу Заняття 1 – 2
- •Заняття 3 – 4
- •Заняття 5 – 6
- •Заняття 7 – 8
- •Заняття 9 – 10
- •Заняття 11 – 12
- •Заняття 13 – 14
- •Заняття 15 – 17
- •Заняття 18 -20
- •Заняття 21 – 22 Модуль в рівняннях з параметрами
- •Заняття 25 – 26
- •Заняття 27 – 30
- •Заняття 31 – 32
- •Заняття 33 – 34
Заняття 21 – 22 Модуль в рівняннях з параметрами
Відпрацювання навичок розв’язування рівнянь з параметрами, що містять модуль алгебраїчним способом.
Вправа 64. Розв’язати рівняння залежно від параметра а:
а) ![]()
б) ![]()
Розв’язання
а)
,
![]() .
.
![]() ,
,
![]() .
.
![]()
Якщо
, то ![]() .
.
![]() або
або ![]()
![]() або
або ![]()

Якщо ![]() ,
то рівняння немає коренів; якщо
,
то рівняння має один корінь
,
то рівняння немає коренів; якщо
,
то рівняння має один корінь ![]() ;
якщо
;
якщо ![]() ,
то рівняння має два корені
,
то рівняння має два корені ![]() та
та ![]() .
.
Відповідь.
Якщо : немає коренів;
якщо : ;
якщо : , .
б)
Розв’язання
Якщо а=1, то рівняння має безліч
коренів ![]() ;якщо
,
то рівняння матиме один корінь, який
знайдемо із систем
;якщо
,
то рівняння матиме один корінь, який
знайдемо із систем
![]()
Отже, ![]() при
,
при
,
![]() при
при ![]()
Відповідь. якщо а=1: ![]()
якщо : ;
якщо ![]() .
.
Завдання для самоперевірки
Вправа 65. Розв’язати
при всіх а рівняння
![]()
Вибрати правильну відповідь:

Вправа 66. Розв’язати
при всіх р
рівняння:
![]()
Вибрати правильну відповідь:

Вправа 67. Розв’язати
при всіх а
рівняння:
![]()
Вибрати правильну відповідь:

Вправа 68. Знайти
всі а ,
при яких рівняння
![]() має
рівно один розв’язок.
має
рівно один розв’язок.
Вибрати правильну відповідь:

Контрольні завдання
Вправа 69. Розв’язати
при всіх а
рівняння
![]()
Відповідь.

Вправа 70. Знайти
всі значення параметра а, при яких
рівняння
![]() має рівно один розв’язок.
має рівно один розв’язок.
Відповідь.![]()
Розв’язати рівняння з перебором
Вправа 71. Розв’язати
при всіх а рівняння:
![]()
Розв’язання:
В залежності від знака виразу
![]() розглянемо два випадки:
розглянемо два випадки:
Випадок 1.
![]()
Випадок2.
![]()
Відповідь.
Вправа 72. Розв’язати
при всіх b
рівняння:![]()
Розв’язання:
Оскільки в правій частині
параметра немає, то зручно розглянути
два випадки в залежності від знаку
правої частини
![]()
Випадок 1.
![]()
Випадок 2.
![]()
Відповідь.
Вправа 73. Розв’язати
при всіх р
рівняння:![]()
Розв’язання:
В залежності від знаку виразу
![]() розглянемо
2 випадки:
розглянемо
2 випадки:
Випадок 1.
![]()
Випадок 2.
![]()
Відповідь.
Вправа 74.
Знайти всі а, при яких
рівняння
![]() має рівно один розв’язок.
має рівно один розв’язок.
Розв’язання:
В залежності від знаку виразу розглянемо 2 випадки:
В залежності від знаку правої частини рівняння 2х можливі два випадки:
Випадок 1.
![]()
Випадок 2.
![]()
Відповідь.
Тренувальні вправи
Вправа 75. Розв’язати
при всіх а
рівняння
![]()
Вибрати правильну відповідь:

Вправа 76. Розв’язати
при всіх b
рівняння
![]()
Вибрати правильну відповідь:

Заняття 25 – 26
Тема: Раціональні рівняння з параметрами
Вправа 77. В
залежності від значення параметра а
визначити число коренів рівняння ![]() .
.
Розв’язання
Дане рівняння є раціональним
рівнянням четвертого степеня, отже,
може мати не більше 4 коренів. Нехай ![]() ,
перепишемо рівняння у вигляді
,
перепишемо рівняння у вигляді ![]() .
.
Вихідне рівняння має 4 корені, якщо останнє квадратне рівняння має 2 різні додатні корені. Достатні умови цього записані у вигляді системи (вітки параболи направлені в гору):
 звідки слідує:
звідки слідує: ![]() .
.
Якщо один із коренів ![]() а другий корінь
а другий корінь ![]() ,
то вихідне рівняння буде мати 3 корені.
Запишемо умови цього випадку:
,
то вихідне рівняння буде мати 3 корені.
Запишемо умови цього випадку:
 звідки слідує, що
.
звідки слідує, що
.
Вихідне рівняння по змінній
х буде мати 2 корені ![]() , якщо один із коренів
, якщо один із коренів ![]() а другий корінь
.
Умовою цього випадку буде нерівність
а другий корінь
.
Умовою цього випадку буде нерівність
![]() ,
або
,
або ![]() .
.
Крім цього, якщо ![]() , то вихідне рівняння також має 2 корені
, то вихідне рівняння також має 2 корені
![]() .
.
Розглянемо тепер випадок,
коли
а другий корінь ![]() .
Тоді вихідне рівняння по змінній х буде
мати єдинний корінь
.
Тоді вихідне рівняння по змінній х буде
мати єдинний корінь ![]() .
Достатньою умовою цього є система:
.
Достатньою умовою цього є система:
![]()
![]()
І нарешті, вихідне рівняння не буде мати розв’язків в двох випадках: або коли обидва корені від’ємні і другий корінь ; або коли коренів у квадратного рівняння взагалі немає, тобто . Достатня умова відсутності коренів визначається сукупністю
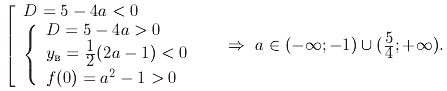
Відповідь. Якщо ![]() : 4 корені;
: 4 корені;
якщо : 3 корені;
якщо ![]() : 2 корені;
: 2 корені;
якщо : 1 корінь;
якщо ![]() : коренів немає.
: коренів немає.
Вправа 78. При яких значеннях параметра а нерівність
![]() немає розв’язків, більших 1?
немає розв’язків, більших 1?
Розв’язання
Приведемо
нерівність до вигляду ![]() .
Оскільки дискримінант чисельника
.
Оскільки дискримінант чисельника ![]() для будь-якого а, запишемо
рівносильну нерівність
для будь-якого а, запишемо
рівносильну нерівність ![]() ,
де
,
де
![]() ;
;
![]() .
.
Розв’язуючи
останню нерівність методом інтервалів,
приходимо до висновку, що умова задачі
буде виконуватися тільки при такому
розміщенні точок ![]() ,
а на осі абсцис, при якому сумісна
система нерівностей:
,
а на осі абсцис, при якому сумісна
система нерівностей:
![]()
![]() .
.
