Устойчивость автоматических систем

У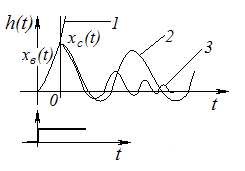 стойчивость АСР является необходимым условием их применения. Пусть система находится в равновесии. Затем она была выведена из этого состояния под действием возмущения. Движение системы под действием возмущения называется вынужденным. Обозначим как x_в(t). В какой-то момент времени эти возмущения были скомпенсированы или устранены. Примем это время за начало отчета (t=0). С этого момента начинается свободное движение системы. Обозначим как x_c(t). Переходный процесс при этом будет являться суммой вынужденных и свободных движений:

h(t) = x_в(t) + x_c(t).

АСР устойчива, если при свободном движении она возвращается к исходному или близкому к нему установившемуся (равновесному состоянию). Неустойчивая система не возвращается к состоянию равновесия. Если система совершает около равновесного состояния недопустимо большие колебания, то такая система находится на грани устойчивости.

lim x (t) = 0 - система устойчива;

lim x (t) = const - система нейтральная (или на грани устойчивости);

lim x (t)   - система неустойчива.

Наглядно это устойчивость можно продемонстрировать на следующем примере:

устойчивая нейтральная неустойчивая

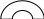
Об устойчивости системы в обобщенном виде можно судить по теореме А.М. Ляпунова. Свободное движение АСР описывается решением ее дифференциального уравнения с правой частью равной 0 (см. полином).

Это уравнение в преобразованном по Лаплассу виде называется характеристическим уравнением АСР:

Решение этого уравнения в общем виде представляет собой сумму экспонент, показатели степени которых равны произведению корней характеристического уравнения на время:

где m - порядок характеристического уравнения

c - постоянные интегрирования;

p - корни характеристического уравнения и отрицательными.

Анализ выражения показывает, что (t)  0 при t  , если p_i  0

Из этого можно сделать следующие выводы:

1) для устойчивости линейной АСР необходимо и достаточно, чтобы все действительные корни и вещественные части комплексных корней характеристического уравнения были отрицательными;

2) если хотя бы один корней лежит на мнимой оси, то система находится на грани устойчивости;

3) если хотя бы один корней положительный, то система не устойчива.

Критерии устойчивости аср.

Во многих случаях пользоваться вышеприведенным методом при определении устойчивости АСР практически невозможно, т.к. находить корни алгебраических уравнений высоких степеней трудно, а уравнения степеней выше четвертого порядка вообще аналитически не решаются.

В связи с этим в современной теории АСР и инженерной практике нашли широкое применение косвенные методы исследования систем на устойчивость. Эти методы получили название критериев устойчивости.

Алгебраический критерий устойчивости Раусса-Гурвица.

По определению данного критерия система устойчива, если все коэффициенты характеристического уравнения, а также все определители составленные из этих коэффициентов положительны.

Запишем характеристическое уравнение

В определении можно выделить необходимые условия устойчивости, заключающиеся в том, что все коэффициенты должны быть больше нуля, т.е.

a₁ > 0, a₂ > 0,…, a_n-1 > 0, a_n > 0.

Если хотя бы один из коэффициентов равен нулю, то система находится на границе устойчивости, а если хотя бы один из коэффициентов отрицательный, то система неустойчива.

Достаточными условиями устойчивости является то, что все определители характеристического уравнения положительны.

₁ = a₁ >0 ;

₂ = = a₁ a₂ – a₀ a₃ > 0 ;

…………………………………………..

_n = 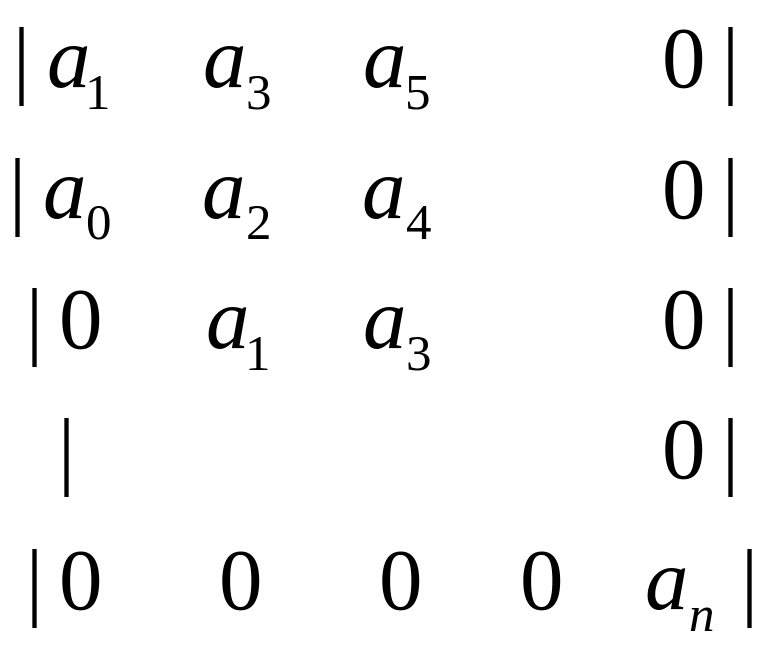> 0

Определители составляются следующим образом: по диагонали от левого верхнего угла к правому нижнему выписываются все коэффициенты по порядку от а₁ до а₂; каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. При отсутствии данного коэффициента, или если его индекс меньше нуля или больше n, на его месте пишется нуль.

Частотный критерий устойчивости Михайлова.

Имеется характеристический полином (уравнение)

Заменим в этом выражении p на j . Получим вектор характеристического полинома

где DRe() - полином членов содержащих j,

DIm() - полином членов не содержащих j.

При изменении частоты   [0,  ] вектор D(j) описывает годограф, который называется годографом Михайлова. Михайлов предложил по виду этой кривой судить об устойчивости системы.

Критерий звучит так: необходимым и достаточным условием устойчивости является условие, когда данный годограф, начинаясь на положительной действительной полуоси, монотонно повернется на угол n/2, где n - показатель степени характеристического полинома, против часовой стрелки, обойдет n квадрантов на комплексной плоскости, не нарушая при этом последовательности прохождения и не пересекая начало координат. Если он пройдет через начало координат, то система находится на границе устойчивости. Если не выполнится хотя бы одно из перечисленных условий требований, то система является неустойчивой.

Годограф Михайлова строится по точкам, задаваясь . Среди точек должны быть найдены точки пересечения точки пересечения с осями координат, которые определяются из условий Re = 0, Im = 0.

Частотный критерий устойчивости Найквиста.

Данный критерий позволяет судить об устойчивости замкнутой системы, охваченной отрицательной статической обратной связью, по АФЧХ разомкнутой этой системы.

С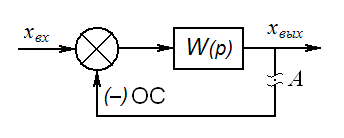 татической является обратная связь, у которой передаточная функция равна 1. Пусть имеется следующая система, которую мы разрываем в точке А.

По определению критерия необходимым и достаточным условием устойчивости замкнутой системы является условие, когда АФЧХ разомкнутой системы не охватывает точку с координатами [-1; 0 ] , т.е. Re = -1, Im = 0. Если кривая проходит через эту точку, то система находится на границе устойчивости, если охватывает – то система является неустойчивой.