Функциональные и структурные схемы аср

Любую АСР, как и устройство можно представить как комбинацию простейших элементов, соединенных между собой и воздействующих друг на друга.

Если система расчленяется по функциональному признаку (по роду выполняемых функций элементами), то получаются функциональные схемы. При этом каждый элемент изображается в виде прямоугольника, внутри которого проставляется его функциональное обозначение. Те воздействия которые элементы оказывают друг на друга изображаются стрелками или линиями.

Пусть Q_п, Q_н – расходы подачи газа и нагрузки на ОУ, Х_р – сигнал с регулирующего устройства; l – перемещение подвижного органа.

Пневматическое исполнительное устройство (МИМ), установленное на трубопроводе . Оно состоит из исполнительного механизма (ИМ) и регулирующего органа (РО) , т.е. устройство имеет два функциональных блока и его функциональная схема будет выглядеть следующим образом:

Если в данном примере трубопровод принять за объект управления, то данная система регулирования расхода будет представлена в виде следующей функциональной схемы

Если АСР разбивается по динамическому принципу, т.е. происходит изменение сигнала по времени, то имеет место структурная схема.

Структурные схемы состоят из динамических звеньев, узлов суммирования, и узлов разветвления. Динамические звенья изображаются в виде прямоугольника, внутри которого записывается передаточная функция звена. Узел суммирования выполняется в виде знака суммирования , узел разветвления в виде точки. Эти элементы соединяются между собой стрелками, показывающими направление прохождения сигнала.

При прохождении сигнала через узел разветвления значение его на выходе не изменяется, т.е.

х_вх = х_вых1 = х_вых2 = х_вых3 = … = х_выхn

При прохождении сигналов через узел суммирования их значение на выходе суммируется, т.е.

х_вых = х_вх1 + х_вх2 + х_вх3 + … + х_вхn

Динамические звенья

При прохождении сигнала через динамическое звено он изменяется как по величине, так и форме.

Звенья классифицируются по динамическим свойствам, т.е. по уравнению связи между входным и выходным сигналами, что позволяет:

- не учитывать функциональную сущность процесса;

• не учитывать конструктивное исполнение устройства.

Динамические звенья, описываемые уравнениями не выше второго порядка, носят название типовых.

Основными типовыми звеньями являются:

- усилительное;

- инерционное;

- колебательное;

- интегрирующее;

- дифференцирующее идеальное;

- дифференцирующее реальное;

- запаздывающее.

Типовые динамические звенья

Усилительное (безинерционное) звено.

Уравнение связи имеет следующий вид x_вых = k x_вх,

где k – коэффициент пропорциональности (усиления).

П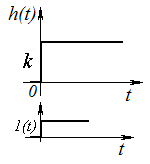 ри единичном ступенчатом воздействии x_вх = 1(t) переходный процесс описывает следующее выражение

h(t) = k 1(t) .

При прохождении сигнала через звено его форма не изменяется, а лишь меняется его величина. Звено не задерживает сигнал, мгновенно пропуская его к выходу. Поэтому звено является безинерционным.

В реальных системах таких звеньев нет. Обычно в АСР принимают за такие звенья те, у которых инерционность значительно меньше чем у других.

Передаточная функция звена имеет следующий вид W(p) = k.

Статическая и динамическая характеристика усилительного звена совпадают, и поэтому такое звено является статическим.

Инерционное звено (апериодическое первого порядка).

Уравнение связи имеет следующий вид

где T – постоянная времени объекта.

При единичном ступенчатом воздействии x_вх = 1(t) переходный процесс описывает следующее выражение

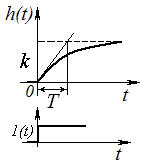h(t) = k (1-e^-t/T) .

Переходный процесс носит не колебательный характер, постоянно (асимптотически) приближаясь к новому равновесному состоянию. Поэтому звено называется инерционным. Чем больше постоянная времени, тем звено более инерционно.

Передаточная функция звена имеет следующий вид

При t   . Уравнение связи будет описываться как

x_вых = k x_вх..

Следовательно, уравнения статики и динамики совпадают и такое звено является статическим.

Колебательное звено (апериодическое второго порядка).

Уравнение связи имеет следующий вид

где T₁, T₂ – постоянные времени объекта.

Если T₁/T₂  2, то имеет место колебательное звено. Если T₁/T₂  2, то имеет место инерционное звено второго порядка. При единичном ступенчатом воздействии x_вх = 1(t) переходный процесс описывает следующее выражение

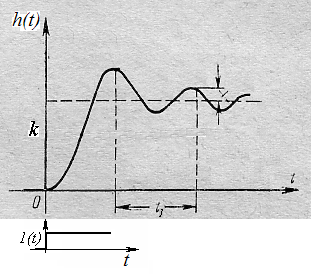
h(t) = k{1-e^-t[cost + (/)sint]},

где  = T₂/2T₁² ; – частота изменения сигнала

где t = 2 - период затухания колебаний.  = 2T₁/T₂

Т.е. при прохождении через звено сигнал, колеблясь относительного нового равновесного состояния с течением времени, затухает, поэтому звено периодическое инерционное.

Передаточная функция звена имеет следующий вид

При t   и .

Уравнение связи будет описываться как x_вых = k x_вх..

Следовательно, уравнения статики и динамики совпадают и такое звено является статическим.

Интегрирующее звено.

Уравнение связи имеет следующий вид

Это выражение показывает, что скорость изменения выходного сигнала в данном случае пропорционально величине входного.

Уравнение (проинтегрировав) можно записать в следующем виде

.

Поэтому оно носит название интегрирующего.

П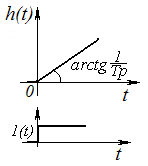 ри единичном ступенчатом воздействии x_вх = 1(t) переходный процесс описывает следующее выражение

h(t) = kt,

При прохождении через звено сигнал монотонно возрастает и не имеет определенного равновесного состояния. Следовательно такое звено является астатическим. Только в случае, когда x_вх. = 0, то x_вых = const, т.е. при нулевом значении входа выходной сигнал принимает то значение на котором наступило равновесие.

Передаточная функция звена имеет следующий вид

(Иногда уравнение связи интегрирующего звена записывают в следующем виде , где , и, следовательно, передаточная функция запишется как .)

Дифференцирующее идеальное звено.

Уравнение связи имеет следующий вид

П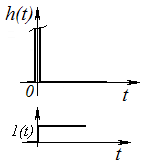 ри единичном ступенчатом воздействии x_вх = 1(t) переходный процесс описывает следующее выражение .

Данное звено не пропускает сигналы, т.е. и x_вых = 0 и только в момент времени t = 0 появления входного воздействия имеет место импульс выходного сигнала.

Передаточная функция звена имеет следующий вид

Дифференцирующее реальное звено.

Уравнение связи имеет следующий вид

П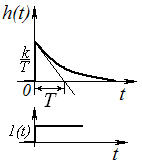 ри единичном ступенчатом воздействии x_вх = 1(t) переходный процесс описывает следующее выражение .

Передаточная функция звена имеет следующий вид .

Следовательно, это звено можно представить как последовательное соединение инерционного звена первого порядка (с передаточной функцией ) и дифференцирующего идеального звена с коэффициентом усиления равным 1 (с передаточной функцией .)

Откуда выражение для общей передаточной функции примет вид

.

Данное звено не пропускает сигнал. При появлении входного сигнала он поступает на инерционное звено первого порядка и в момент времени t = 0 выходной сигнал возрастает до величины k/T. Далее он поступает на дифференцирующее идеальное звено и поэтому резко асимптотически уменьшается, стремясь к оси абсцисс.

Запаздывающее звено.

Уравнение связи имеет следующий вид

где  – время запаздывания.

При единичном ступенчатом воздействии x_вх = 1(t)

переходный процесс описывает следующее выражение h(t) =1 (1-) .

П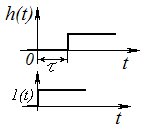 ри прохождении через звено сигнал не меняет своего значения и формы, только сигнал выхода отстает от входного на отрезок времени . (Пример - длинный трубопровод.)

Передаточная функция звена имеет следующий вид .

Если в передаточной функции заменить комплексную переменную р на j, то выражение оно будет выглядеть как

по формуле Эйлера = cos  jsin .

Откуда Re() = cos и Im ()=-sin . Тогда