Регулирующие органы

РО называется звено ИУ, воздействующее непосредственно на процесс в объекте управления путем изменения пропускной способности.

Пропускная способность – это расход вещества или энергии, проходящего через РО. Конкретно для вещества – это его расход при определенном перепаде давления и выражается в м³/час.

Основными РО являются клапаны, заслонки, шиберы.

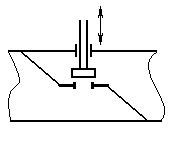
Клапаны (дроссельные РО) применяются для жидкостей и газов. Бывают одно и двух седельные, шланговые, мембранные.

З аслонки применяются для газа, пара, твердых частиц (гранул). Основной элемент круглый диск или диск двоякой кривизны.

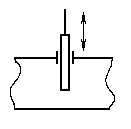
Шиберы (задвижки) применяются для жидкостей и газов. Основной элемент затвор.

Основы теории автоматического управления Статика и динамика системы

АСР - может находиться в равновесном (статическом) и неравновесном (динамическом) состояниях.

Статическая характеристика определяется выражением

х_вых = f(х_вх)  _{  } ;

Динамическая характеристика имеет следующий вид х_вых = f(х_вх, ).

Эти характеристики как правило нелинейны и для их реализации требуется сложный математический аппарат. Поэтому на практике проводят линеаризацию, т.е. в некоторой точке или на определенном интервале нелинейные характеристики приближенно считаются линейными.

Линейные АСР описываются линейными уравнениями. Линейная статическая характеристика имеет следующий вид

х_вых = k f(х_вх)  _{  }

Линейная динамическая характеристика описывается полиномом производных различной степени:

где A₀, A₀₁,…, A_m, и B₀, B₁,…, B_n - постоянные коэффициенты, определяемые свойством АСР.

При х_вых = 0, т.е. когда сигналы отклонения или возмущающего воздействия устранены, имеет место однородное линейное уравнение, которое характеризует поведение системы уравнений при свободном движении.

Преобразование Лапласса. Передаточные функции.

Преобразование Лапласса существенно облегчает решение уравнений вида (1), т.к. позволяет заменить дифференциальные уравнения на алгебраические. При этом в результате применения интегрального преобразования Лапласса к уравнению динамики функция f вещественного переменного (времени ) преобразуется в функцию F комплексного переменного (p).

p =   ,

где  - постоянный коэффициент,  - мнимая единица (² = -1).

Функция вещественного переменного f () называется оригиналом функции, функция комплексного переменного F(p) - изображением оригинала. Любому оригиналу функции соответствует его изображение f() = F(p),

которое определяется по таблицам или формуле перехода

F(p) =  f()e^-p d.

Для замены оригинала его изображением существует правило дифференцирования: операция дифференцирования вещественного переменного соответствует оператору умножения преобразования простейшей функции на комплексную переменную соответствующей степени:

f() = F(p),

f ^I() = F(p)p,

f ^II() = F(p)p²,

f ^III() = F(p)p³



f ⁿ() = F(p)pⁿ.

Применив правило к уравнению (1) получим:

A₀x_вых(p)p^m + A₁x_вых(p)p^m-1 + …+ A_m-1x_вых(p)p + A_mx_вых(p) =

= B₀x_вх(p)pⁿ + B₁x_вх(p)p^n-1 + …+ B_n-1x_вх(p)p + B_nx_вх(p).

Или

x_вых(p)(A₀p^m + A₁p^m-1 + …+ A_m-1p + A_m) = x_вх(p)(B₀pⁿ + B₁p^n-1 + …+ B_n-1p + B_n)

Очень удобно при исследовании АСР представлять связь входной и выходной величин с помощью передаточной функции.

Передаточная функция W(p) - это отношение изображения оригинала выходного сигнала к изображению оригинала входного сигнала при нулевых начальных условиях. Передаточная функция определяется по конечному выражению, т.е.

.

Знаменатель передаточной функции называется характеристическим полиномом

.