1. Сложение (вычитание) вида:

30 + 20 = 50

3 дес. + 2дес. = 5 дес.

60 - 20 = 40

6 дес. – 2 дес. = 4 дес.

Теоретическое обоснование: разрядный состав числа, таблица сложения (вычитания) в пределах 10.

2. 3 6 + 2 =

30 6

30 + (6 + 2) = 38

Заменю 36 суммой разрядных слагаемых 30 и 6, получу:

(30 + 6)+2

Удобнее единицы складывать с единицами и полученный результат прибавить к десяткам:

30 + 8 = 38

Читаю ответ: сумма равна 36.

Теоретическое обоснование: разрядный состав числа, сочетательное свойство сложения, сложение в пределах 10.

Аналогично: 30 + 24 и 26+4.

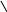3. 36 – 2

30 6

Заменю 36 суммой разрядных слагаемых 30 и 6.

Удобнее из единиц вычитать единицы, из 6 вычитаем 2, получим 4 и к 30 прибавим 4, разность равна 34.

3 0 - 4

20 10

Заменю число 30 суммой удобных слагаемых 20 и 10.

Удобнее из 10 вычесть 4 и к20 прибавить 6.

Читаю ответ.

Обязательна наглядность.

Теоретическое обоснование: разрядный состав числа, правило вычитания числа из суммы, вычитание из 10, представление числа в виде суммы удобных слагаемых.

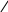
4. 6 0 - 24 =

20 4

Заменяю 24 суммой разрядных слагаемых

(60 - 20) - 4 = 26

Удобнее из 60 вычесть…

Теоретическое обоснование: разрядный состав двузначного числа, вычитание числа по частям, вычитание суммы из числа, вычитание в пределах 10

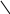5. 2 6 + 7

4 3

(26 + 4) +3 = 33

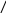
6. 3 5 - 7

5 2

(35 – 5) – 2 =

7. Остальные случаи рассматриваются на основе письменного сложения (вычитания) столбиком (смотри таблицу).

Упражнения для закрепления:

1. Комментарии решения примеров.

2. Объяснения решения примеров (можно с ошибкой).

3. Самостоятельное решение примеров с подробной проверкой.

4. Составление учащимися примеров и решение их.

Формирование вычислительных умений

(сложение и вычитание в пределах 100) – Истомина Н.Б.

Процесс формирования вычислительных умений - это усвоение общего способа действий. Дети должны знать:

1. Запись чисел в десятичной системе исчисления (разрядный состав числа).

2. Смысл действий сложения и вычитания.

Способ введения вычислительного приема

1. Выполнение действий с моделями десятков и единиц

2. Соотнесение этих действий с математическими записями.

3. Наблюдение изменения цифр, обозначающих в записи числа десятки (единицы) при увеличении (уменьшении) числа на несколько десятков (единиц).

М 1 И. с. 134-135

Используется прием анализа, синтеза, сравнения, классификации, обобщения. Система заданий помогает детям самим «открывать» общий способ действий и овладевать вычислительными умениями.

Для усвоения приема вычислений используются различные виды моделирования:

1. Предметное моделирование:

2. Схематическое моделирование

3 6 + 2 =

30 6

3. Символическое моделирование

36 + 2 = 30+ (6+2) = 38

Развернутое отражение операций.

Изучение таблиц умножения и соответствующих случаев деления

Современная методика требует, чтобы дети поняли принципы составления таблицы, которые дают возможность находить результат кратчайшим путем.

Какие случаи умножения называют табличными?

Приемы вычисления табличных результатов.

1. Сложение 2*3 = 2+2+2=6

2. Использование ответа предыдущего примера из таблицы умножения для нахождения результат следующего примера. Прибавлять данное число к предыдущему результату.

2*5 = 10 2*6 = 10+2

3. Перестановка множителей 2*4 = 8 4*2=8

4. Использование взаимосвязи компонентов и результатов арифметических действий умножения и деления (Если произведение разделить на один множитель получим второй множитель).

Табличные случаи умножения на 2, на 3 начинают усваивать в процессе изучения а) смысла умножения, б) переместительного свойства умножения, в) понятия увеличить в несколько раз, д)сочетательного свойства умножения.

Результаты этой работы подводятся в теме «Таблица умножения», где предлагаются задания для проверки усвоения таблицы умножения.

Усвоение табличных случаев деления распределено по времени:

А) усвоение смысла деления; б) правила взаимосвязи компонентов и результатов действий умножения и деления; в) уменьшения в несколько раз, г) кратное сравнение. ????

Табличные случаи умножения и соответствующие им случаи деления должны быть усвоены учащимися на уровне навыков.

Выделено 2 основных этапа:

1. Составление таблицы

2. Усвоение таблиц (т.е. прочное запоминание)

Для составления таблиц учащиеся должны усвоить теоретические вопросы:

А) Смысл действия умножения как сложения одинаковых слагаемых;

Б) Переместительное свойство умножения;

В) Взаимосвязь компонентов и результатов умножения;

Д) Смысл деления;

Найти в учебнике М2ч. 2кл. Моро теоретические вопросы, которые должны усвоить учащиеся.

Последовательность составления таблиц и организация деятельности, направленной на их составление может быть различной.

(М 2ч., 2кл. Моро с. 68 и 3 кл. ч. 1 с. 18 – предыдущее издание)

1. Умножение числа 2, умножение на 2.

Рассматриваем наглядно и предлагаем запомнить:

1 урок 2*2 = 4 3*2 = 6 4*2 = 8 5*2 = 10

2 урок 6*2 = 12 7*2 = 14 8*2 = 16 9*2

3 урок: деление на 2

3 *2 = Соотнесение рисунка с математической записью

6: 2 = 9*2 =

6: 3 = :2 =

: 9 =

Аналогично рассматривается умножение числа 3, на 3,деление на 3

Рассматриваются ???? действия умножения, названия компонентов и результатов действий. С.20

II. Усвоение табличных случаев умножения и деления с числами 2 и 3 распределено по времени, что способствует формированию вычислительных навыков.

Основная таблица составляется по постоянному первому множителю, иллюстрируется наглядно как результат сложения.

Таблица умножения постоянному первому множителю начинается с умножения одинаковых множителей.

Вторая таблица использует переместительное свойство умножения (постоянный второй множитель).

Третья таблица: использует взаимосвязь между компонентом и результатом действия умножения, используя 1 столбик.

Четвертый столбик: тоже самое, что третий столбик. (Постоянное значение частного)

Задание: Используя учебник М3 М ч. 1 опишите, как организовать деятельность учащихся при составлении таблицы умножения (деления) с числами 4, 5, 6ю

Составляется таблица Пифагора, с. 50 (столбики, строки)

Сводная таблица с. 79 (20 случаев)

Также составление таблиц умножения и деления позволяет осознать взаимосвязь этих действий.

Дети заучивают таблицу с большим трудом. Учебного времени не хватает. Учителю необходимо организовать работу по заучиванию таблицы. Для этого необходимо разнообразить упражнения, предлагать их в игровой форме. Ежедневно у каждого ученика спрашивать таблицу и предлагать меньший объём для заучивания.

Есть и другие подходы к изучению таблицы. Таблица распределена не по столбикам, а по строкам, каждая из которых включает 4 случая.

4*5 =

5*4 =

20:4 =

20: 5=

Истомина Н. Б.

Работа с учебником.

1. Выделение признаков сходства и различия данных выражений. (Чем похожи? Чем отличаются?)

2*7 7*2

2. Соотнесение рисунка и числового выражения.

2*2 4:2

3. Запись числового выражения по данному рисунку

6:2 4:2 6:3

4. Замена произведения суммой.

2*6 = 2+2+2+2+2+2

5. Сравнение числовых выражений.

2*6 и 6*2

3*4 и 6*2

Начинается заучивание таблицы со случая умножения числа 9 (Постепенно, в течение 12 уроков)

В обучающих заданиях даются установки на запоминание 3-4 табличных случаев в определенной последовательности (не подряд):

А) 9*5; 9*6; 9*7;

Б) 9*2; 9*3; 9*4;

В) 9*8; 9*9; 9*7

Для организации самостоятельной работы по усвоению табличного умножения можно каждый случай фиксировать на каточке

1 сторона Обратная сторона

9*5 45

Аналогично для случаев табличного деления.

Можно показать детям таблицу умножения числа 9 на пальцах.

При изучении таблицы умножения с числом 9 можно проиллюстрировать пучками – десятками палочек.

9*2 = 18

2 десятка без 2-ух: 20-2=18

Составляя таблицу замечаем, что число десятков в ответе на 1 меньше, второго множителя, а сумма цифр в записи ответа равна 9.

Таблица Пифагора. Дети запоминают самостоятельно.

Обратите внимание, как заполнена 1 строчка, первый столбик? Как найти ответ умножения? Деления?

Какие игры и упражнения помогут заполнить таблицу:

- молчанка

-поймай мяч

- забей гол в числовые ворота

- заполни ромашку

-примеры ребусы

-угадай

-конвертик

-телеграф

Деление с остатком

Задачи изучения темы:

1. Раскрыть конкретный смысл деления с остатком, используя отношения между делителем и остатком (схематические рисунки).

2. Раскрыть алгоритм (правило) выполнения деления с остатком:

а) 22:4

22 не делится на 4. Самое большое число до 22, которое делится на 4 – это 20. Разделим 20 на 4, получим 5. Вычтем 20 из 22, получим остаток 2.

22:4=5 (ост. 2)

Остаток меньше, чем делитель.

Б) 31:4

Находим частное более эффективным способом подбора. Пробую 7, 4*7= 28, получается остаток 31-28=3. Сравниваем остаток и делитель. 3 меньше, чем 4, значит подобранное число подходит.

3. Сформировать умение выполнять и записывать деление с остатком и проверять правильность выполнения действий. Дети могут пользоваться любым способом. Учащиеся должны усвоить:

а) что, остаток при делении всегда должен быть меньше делителя;

б) связь между табличным делением, внетабличным делением и делением с остатком;

в) деление меньшего числа на большее.

1. Подготовительная работа.

Постановка учебной задачи:

- 12 тетрадей раздай по 3. Сколько детей получили по 3 тетради?

- 11 тетрадей раздай по три. Сколько осталось тетрадей?

- Нарисуй 9 кружков.

9 кругов разделили по 4. Сколько раз по 4 получилось? Сколько осталось?

2. Раскрытие смысла деления (открытие новых знаний детьми). Знакомство с новой записью.

П рактические упражнения. Установление соответствия между предметным действием (рисунками, предметами) и математической записью. Используется прием сравнения, выбора, преобразования.

6:3=2

7:3=2 (ост. 1)

Сколько раз по три получится? Сколько осталось? Как это записать?

Учимся записывать и читать запись. Выполнение задания с комментированием (внешняя речь). Выписать задания из учебника.

Сравниваем деление с остатком и без остатка. Предлагаем задания на соотнесение рисунка математической записи. Обращаем внимание на остаток.

Вывод: при делении одних чисел остаток получается, а при делении других он равен 0.

3. Р аскрытие отношения между делителем и остатком (наглядно-практически).

7:2=3 (ост. 1)

8:2=4 (ост. 0)

9:2=4 (ост. 1)

Сравниваем делитель и остаток.

- Какие остатки получаются при делении на 2?

- Может ли в остатке получится 2?

- Почему?

Выполняем еще 1-2 задания и делаем вывод:

Остаток при делении всегда меньше делителя.

Первичное закрепление.

1. Выполнение заданий с подробным объяснением учениками.

2. Решение примеров с ошибкой, объяснение причины ошибки, работа в парах (карточки на пару 2 примера, дети объясняют решенные примеры).

3. Самостоятельная работа с последующей проверкой.

-Какие остатки могут быть при делении на 5, 6, 9?

- Может ли при делении на 5 получится остаток 6, 2, 11? Почему?

- Вставь пропущенные цифры:

3 6 : = (ост. 1)

: 8 = (ост. 7)

4. Обсуждаем решение всем классом.

5. Составление примеров и решение их.

4. Знакомство с двумя приемами деления с остатком.

1. Объяснение учителя вместе с классом

23:4

- Делится ли число 23 на 4 без остатка?

- Какое самое большое число делится до 23 без остатка?

- Как можно найти частное?

- Какое число мы разделили на 4?

- Какое число надо было разделить?

- Как найти остаток?

- Какой получится ответ?

23:4

20:4 = 5

23-20 = 3

23:4 = 5 (ост. 3)

2. Второй способ разбора более эффективен. Работа с учебником.

3. Выполнение упражнений для закрепления:

А) объяснение решенных примеров в паре; (с комментированием, внешняя речь);

Б) решение примеров самостоятельно, по вариантам с подробной проверкой (внутренняя речь);

В) решение примеров с окошечками, с объяснением; см. ребусы;

Г) объяснение примеров с ошибкой;

Д) самостоятельное составление аналогичных примеров (Умственное действие).