Элементы теории поля.

Теория поля – крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.

К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы – все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т.д.

Рассмотрим скалярные и векторные поля.

Скалярные поля.

Скалярным полем называется область пространства, если каждой точке М этой области соответствует определенное число U(М).

Другими словами: если в пространстве (х, y, z) имеется область D, в которой задана функция U=U(x,y,z), то говорят, что в обл. D задано скалярное поле.

Пример:

1. если U(x,y,z) – обозначает температуру в точке М, то говорят, что задано скалярное поле температур: в некоторой декартовой системе координат находиться неравномерно нагретое тело и температура его в каждой точке М(x,y,z) известна t˚=U(M). Тогда часть пространства, занятая телом, будет скалярным полем температур данного тела;

2. скалярное поле атмосферного давления, плотности (массы, воздуха), поле влажности;

3. скалярное поле солености воды (устье реки впадающей в море).

Векторное поле

Если каждой точке М области пространства соответствует некоторый вектор , то говорят, что задано векторное поле.

Векторным полем называется область пространства или плоскости, каждой точке которой М(x,y,z) поставлен в соответствие вектор .

, где P(x, y, z), Q(x, y, z) и R(x, y, z) – некоторые функции.

Если поле задано на плоскости, то

Примерами векторных полей являются: поле силы тяжести; поле скоростей частиц текущей жидкости (ветра); магнитное поле; поле напряженностей заряженных объектов и т.д.

Векторное поле называется однородным, если - постоянный вектор, т.е. P,Q,R – постоянные величины.

Таким полем является поле тяжести. Здесь . P=0, Q=0, R=-mg, g - ускорение силы тяжести, m – масса точки.

Векторной линией поля вектора называется такая линия, в каждой точке которой вектор поля направлен по касательной к этой линии.

Для определения уравнения векторных линий поля следует решить систему дифференциальных уравнений .

Для плоского поля

Пример: векторное поле задано вектором . Найти векторные линии, изобразить их и на одной из них построить три вектора.

Решение: составляем дифференциальное уравнение . Это уравнение с разделяющимися переменными. Решаем его и находим уравнения векторных линий.

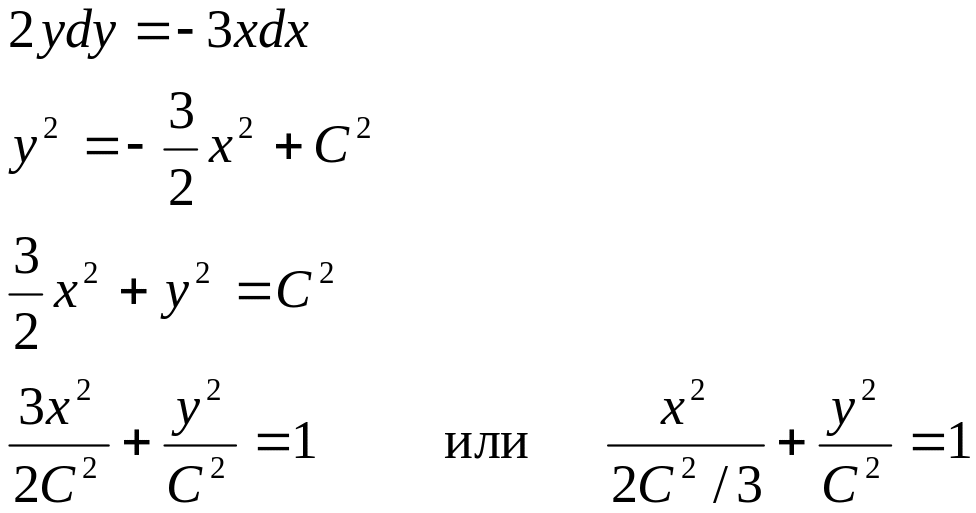
Дадим константе С несколько различных числовых значений :

С=3 - эллипс ( , b=3);

С=5 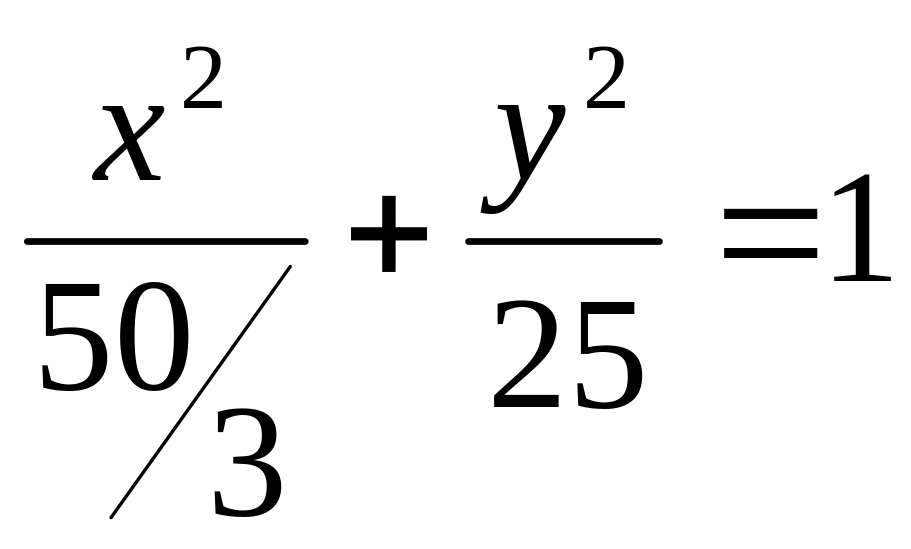- эллипс ( , b=5).

На линии построим три вектора

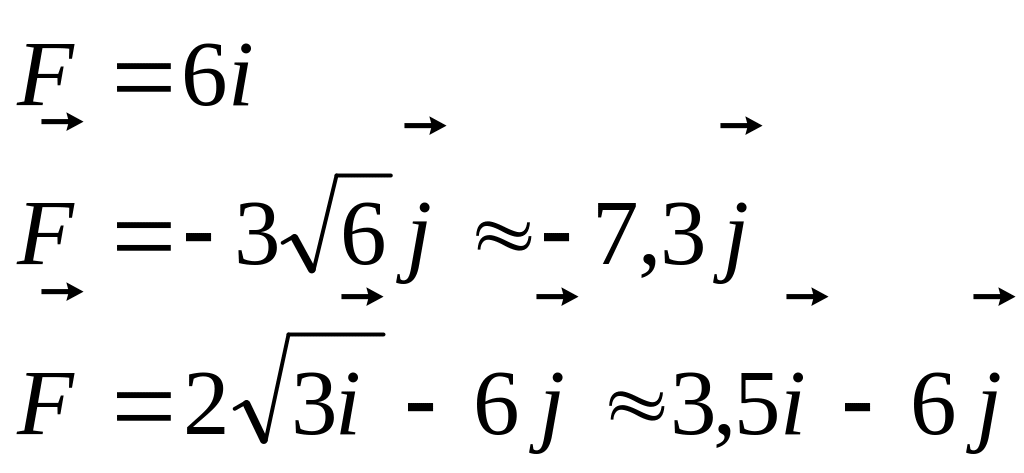
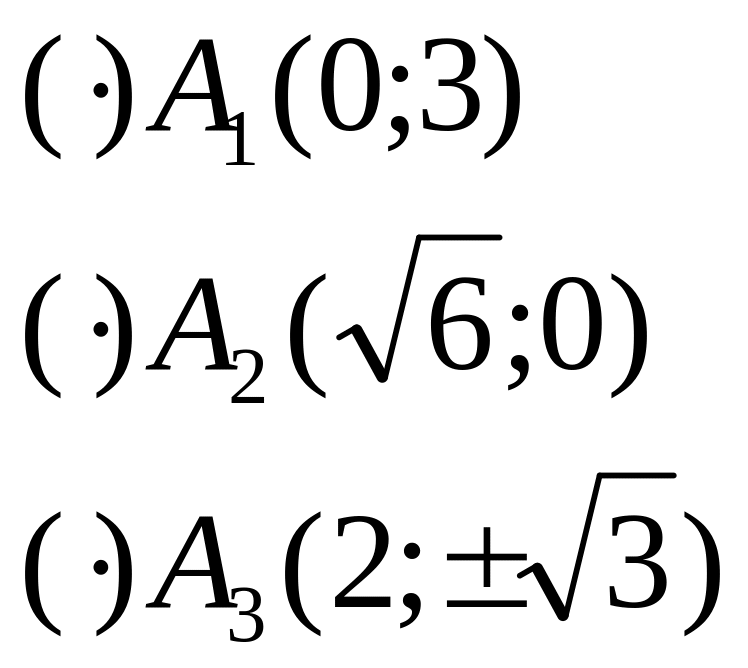В силовых полях векторные линии - это силовые линии, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости (линии тока), для магнитного поля векторными линиями будут линии, выходящие из северного полюса, и оканчивающееся в южном.

Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называются векторной трубкой.