15. Парна регресія. Оцінка лінійної залежності двох змінних

Построение парной регрессии.

1. Постановка задачи:

Пусть имеется N пар выборочных наблюдений за двумя переменными х и у.

Требуется на основе этих выборочных наблюдений статистически оценить у от х и проверить оптимальность полученной оценки.

Зависимость y(x) будем искать

y=f(x)+u где f(x) – функция регрессии

u – случайная остаточная компонента

Функциональная – точная зависимость

Регрессионная – случайная

u обусловлена следующими причинами:

1. Ошибка спецификации. Можно ошибочно не включить важные объясняющие переменные в модель, или использовать агрегированные, обобщенные переменные.

2. Ошибка измерения. Связана со сложностью сбора исходных данных и использование в модели латентных переменных(неявных), которые нельзя измерить непосредственно.

3. Человеческий фактор. Участие человека в сборе и подготовке данных вносит элементы непосредственности.

Относительно u в модель регрессии вносится ряд гипотез, известных как условия Гаусса-Маркова:

1. (мат. ожидание остатка равно 0)

Это требование означает, что не должно быть систематически смещенной ошибки ни в сторону положительных ни в сторону отрицательных значений. Среднее значение случайного остатка должно быть равно 0.

2.

Первая строка полагает, что остатки полученных значений независимы друг от друга

Вторая строка означает постоянство дисперсии остатков, т.е. независимо от того, при каких значениях производится наблюдение.

3. Переменные х(наблюдаемые значения) являются не случайными величинами.

Таким образом задача регрессии имеет вид:

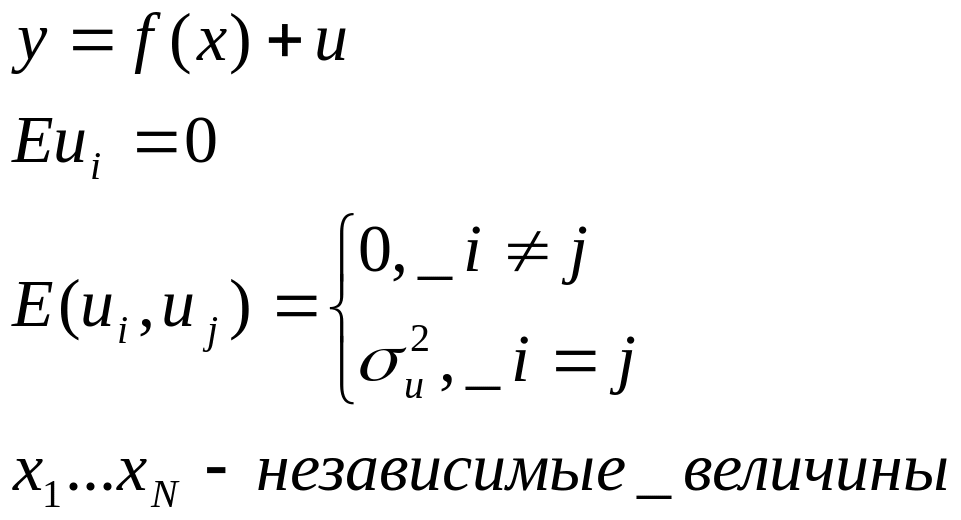
Функция f может быть как линейной так и нелинейной. При выборе ее вида обычно пользуются следующими рекомендациями:

1. Используется априорная информация о содержательной экономической сущности анализируемой зависимости.

2. Предварительный анализ зависимости с помощью визуализации(графический способ)

3. Использование различных статистических приемов обработки данных.

Рассмотрим построение функции регрессии, если полагается линейная зависимость между х и у, т.е. имеем следующую регрессионную модель:

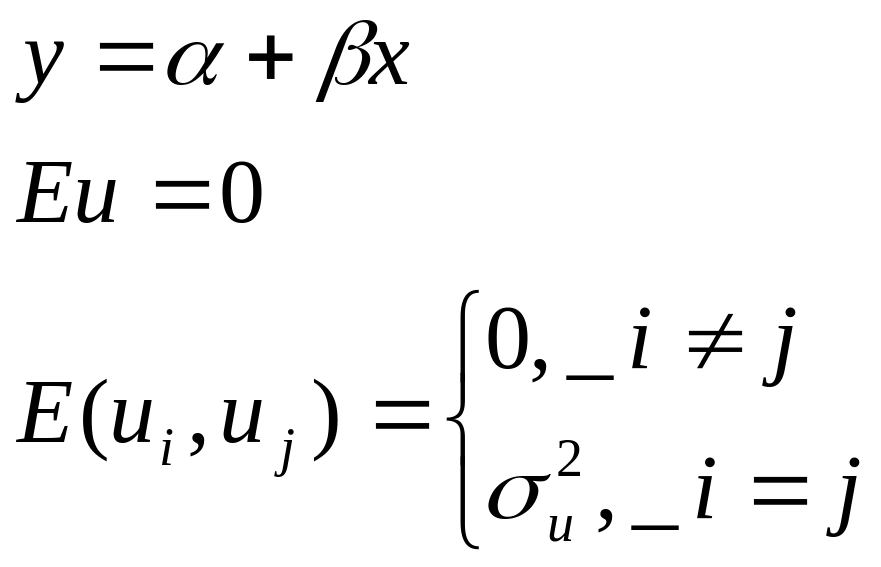
График 5

Неизвестные параметры регрессии и определяются с использованием метода наименьших квадратов.

Принцип МНК заключается в минимизации суммы квадратов отклонений значений.

В i-м наблюдении отклонение между заданными наблюдениями и расчетными(полученным по уравнению регрессии) определяются:

Поэтому общий критерий VYR записываем так:

Необходимое условие минимизации – обращение в 0 частной производной по каждому неизвестному параметру.

Преобразуем систему к такому виду:

Эта система дает искомые оценки параметров и называется стандартной формой нормализации уравнений. Из нее можно получить такие формулы для нахождения и .

где средние значения величин.

Следующая важная проблема регрессионного анализа состоит в том, чтобы определить на сколько хороши полученные оценки коэффициентов и само уравнение регрессии в целом.

Для объяснения линейной связи между переменными можно использовать коэффициент корреляции.

Рассмотрим поле наблюдений

График6

Разобъем наблюдение на 4 квадрата, разместив начало координат в точке , тогда все исходные наблюдения будут пересчитаны по правилу

И тогда понятно, что для точек I и III четверти произведение больше 0 для II и IV -

- эта величина может служить мерой зависимсти между величинами.

Если большая часть точек лежит во I и III четвертях, то сумма имеется линейная положительная зависимость.

Если большая часть точек лежит во II и IV четвертях, то сумма имеется линейная отрицательная зависимость.

Если точки рассеиваются по всем четвертям, то сумма и это означает, что линейных связей между ними нет.

График7

Рассматриваемая мера называется ковариацией и зависит от единиц измерения х и у, поэтому она может принимать разные значения для одних и тех же наблюдений, если они измерены в разных масштабах.

Это является недостатком ковариации.

Если избавить исходное наблюдение от единиц измерения и перейти к стандартизированным данным, например по формуле:

то коэффициент корреляции будет вычисляться по формуле:

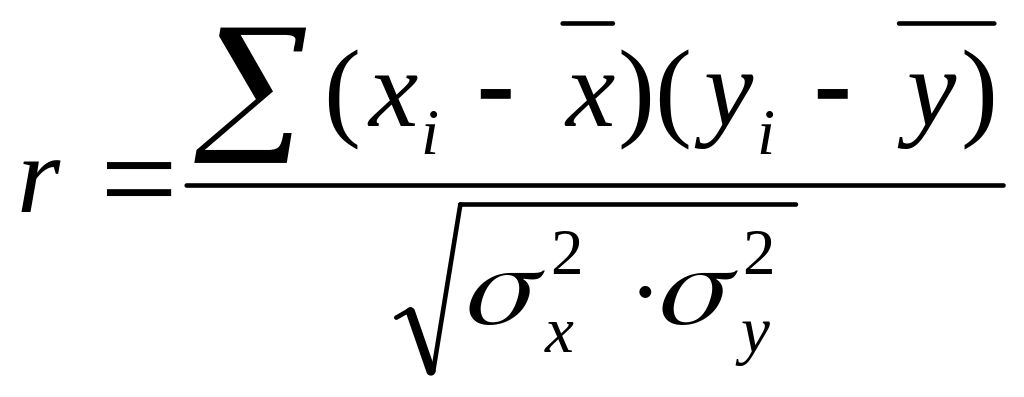
Коэффициент корреляции изменяется от -1 до 1. Если r=1, то сильная линейная положительная связь, если -1, то сильная отрицательная связь, если r=0, то нет линейной связи.

Коэффициент корреляции обладает свойством симметричности

Замечание:

Следует иметь в виду, что коэффициент корреляции ничего не говорит о причинно-следственных связях, поэтому следует избегать так называемых ложных корреляций, т.е. нельзя связать явления между которыми отсутствуют реальные причинно-следственные связи.

Т.о. при построении регрессивной модели необходимо исходить из содержания задачи и анализа причинно-следствия.

Наряду с коэффициентом корреляции рассматривается величина , которая равна и :

Этот показатель называется коэффициентом детерминации и он показывает долю дисперсии y объясненной линейной зависимости от х, чем лучше регрессия соответствует наблюдениям, тем меньше и тем ближе к 1 и наоборот, чем хуже регрессия подогнана к исходным данным, тем ближе к 0.

Коэффициент детерминации используют как меру качества статистического подбора моделей.