12. Лінійні цілочисельні задачі.
Для многих экономических задач логично дополнительное условие целочисленности оптимального решения, например еслиречь идет о производстве недилимой продукции, загрузке оборудования, и т.п.
Оптимизационные задачи, на переменные которых частично или полностью накладываются условия целочисленности называются задачами целочисленного программирования.
ЦФ и ограничения целочисленных задач могут быть как линейными так и нелинейными.
Если в модели только линейные функции, то имеем целочисленную линейную задачу, ее модель в общем виде:
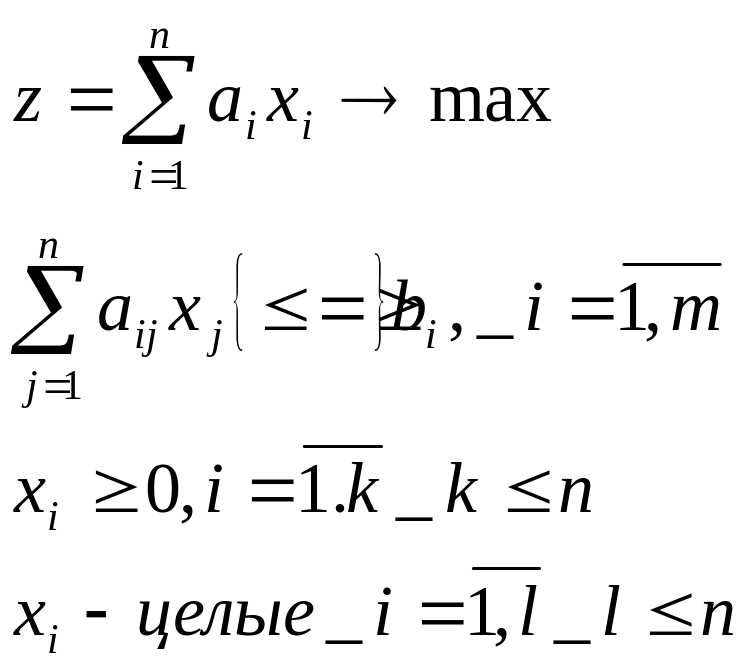
если l=n, то задача полностью целочисленная, если l<n – частично.
Это имеет значение для выбора метода решения.
Линейная целочисленная задача отличается особенной ОДР.
График 1
ОДР задачи целочисленного программирования – система точек с целыми координатами, такая область – не выпуклое и несвязное множество.
Находить оптимальное решение целочисленной задачи округлением нельзя, т.к. полученные целочисленные координаты могут неудовлетворять ограничениям(точка будет вне ОДР) или полученная точка не будет оптимальной. Поэтому для решения целочисленных задач есть специальные методы.
Все существующие методы можно разделить на:
Методы отсечений Гамори
Комбинаторные методы(метод ветвей и границ)
13. Задачі нелінійного програмування.
Большинство моделей экономических задач описываются с помощью нелинейных зависимостей. Такие задачи имеют ряд особенностей, которые нужно учитывать при построении методов решений. В частности: 1) ОДР нелинейной задачи может быть произвольным(не обязательно выпуклым многоугольником); 2) Оптимальная точка задачи нелинейного программирования может находиться в любой точке ОДР.
Алгоритм графического
способа: 1) По ограничениям строим ОДР;
2) Строим линии уровня ЦФ z=const и определяем
направление возрастания; 3) Определяем
координаты оптимальных точек
и
и вычисляем значения ЦФ в них.
Если в задаче содержится более чем 2 переменных и она не сводится к двумерной, то существуют аналитические и численные методы поиска ее экстремума. Самым распространенным аналитическим способом решения является метод Лагранжа.
Его идея заключается к сведению решения условной задачи (с ограничением) к безусловной.
Рассмотрим пример: (ф-ия Бернулли)
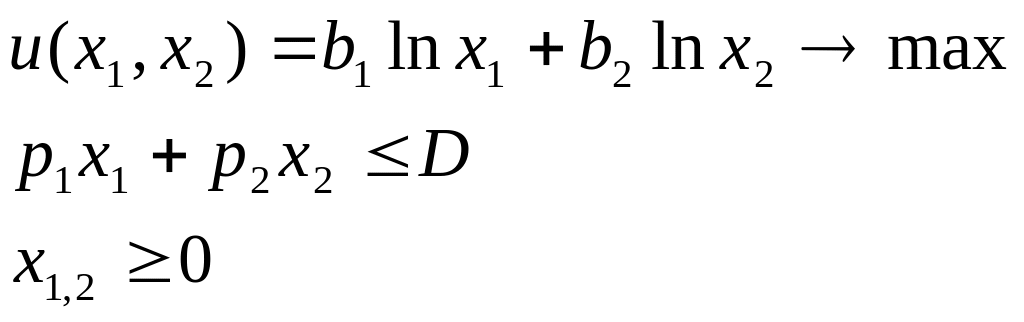
Замечание 1: Метод Лагранжа применим только для задач, в которых ограничения – равенства. График 1.
Т.к. из теории потребления известно, что оптимальная точка лежит на бюджетной линии, то ограничения в данной модели можно записать в виде равенства.
Решаем методом Лагранжа:
1. Строим функцию Лагранжа
- множитель Лагранжа
2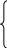
.
Выписываем необходимые условия extr для
функции Лагранжа L
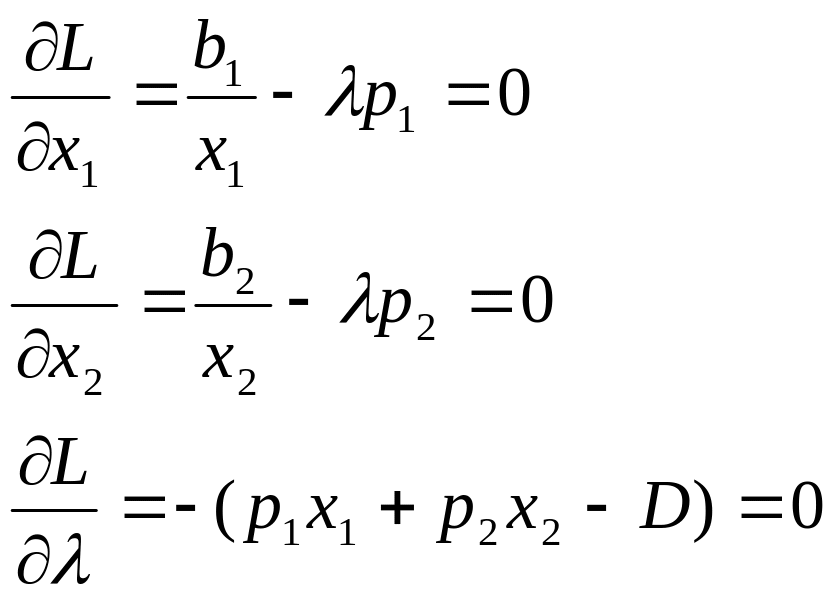
3. Решаем полученную систему уравнений
Подставляем найденный множитель в выражение для Х
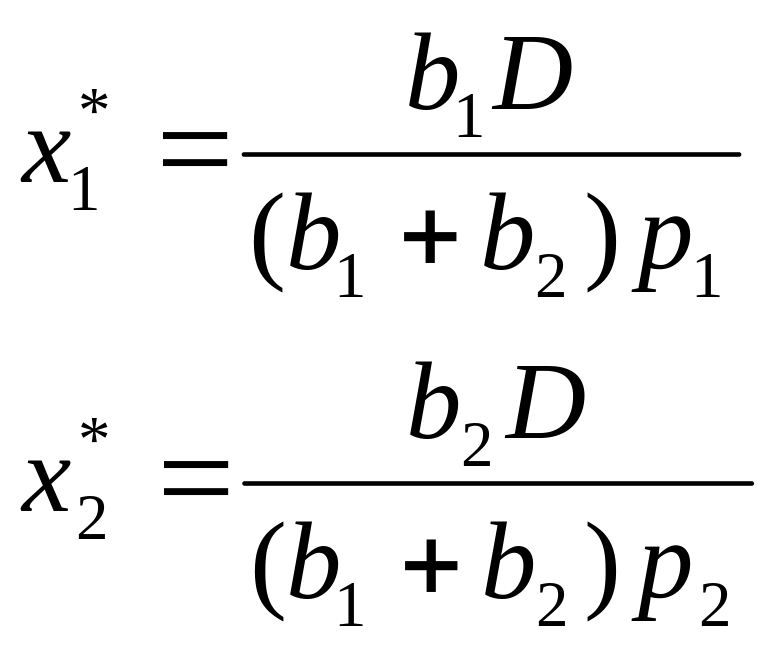
Точка с найденными координатами является точкой extr. Для установления ее характеристик используется матрица 2 производных и исследуется ее характер.
14. Поняття економетричного моделювання. Зв’язок економетрії з іншими науками. Етапи економетричного моделювання.
Эконометрия, как наука охватывает вопросы применения статистических методов к теоретическим моделям, описывающим реальные эк.процессы. Эконометрия в буквальном переводе означает «измерения в эк-ке». Измерения: моделируется связь между разл. параметрами, оцениваются параметры этой связи, её сила, значимость и т.д. Осн.цели эконометрии: 1) выявление объективно-существующих законов и связей между эк.показателями; 2) Модельное описание конкретных кол-венных взаимосвязей, обусловленным качественными закономерностями.
Эконометрия, как самостоятельная наука объединяет совокупность теорет. результатов, приёмов, методов и моделей из разл. наук: 1) Эк. теория. В её рамках выдвигаются какие-либо гипотезы, строятся теории, но подтверждение этих теорет. гипотез и проверка их в конкретных условиях требует применения разл. методов моделирования, в том числе и статистического. Этим и занимается эконометрия; 2) Социально-эк. статистика. Включает информационное обеспечение эк. исс-ий, позволяет решать такие задачи, как выбор необходимых статистических показателей, обоснование способа их сбора, измерений, определение плана статистического исс-ия; 3) Основы ТВМС. Отдельные разделы ТВМС (регрессионный и корреляционный анализ) исп-тся как инструмент для постоения и анализа эконометрических моделей.
Т.о. эконометрия вносит эмпирическое содержание в эк.теорию и позволяет придавать конкретное кол-венное выражение общим качественным закономерностям, обусловленным эк.теорией.
Все этапы эконометрического моделирования можно разделить на 2 группы: 1) Решает проблему спецификации модели. Сюда относят такие этапы: 1.Постановочный (предмодельный анализ на специфические св-ва модели); 2.Априорный (исс-тся хар-ки, как гипотезы); 3.Параметризация (какая модель); 2) Решает вопрос калибровки модели и связана с многократными вычислительными прогонами. Этапы: 4.Информационный (сбор статистики); 5. Идентификация модели (статистическая оценка неизвестных параметров); 6.Верификация модели (проверка на корректность, оценка точности модельных данных).