Теоретичні запитання
Основні аспекти математичного моделювання економіки.
Задача лінійного програмування. Постановка. Геометрична інтерпретація (загальна). Методи розв’язання.
Геометрична інтерпретація задачі лінійного програмування (детальна).
Симплекс-метод. Сутність методу. Основні поняття. Алгоритм.
Аналіз моделей на чутливість.
Двоїстість у лінійному програмуванні. Структура та властивості двоїстих задач.
Перша теорема двоїстості. Її економічний зміст.
Друга теорема двоїстості. Її економічний зміст.
Економічний зміст змінних та обмежень двоїстих задач. Зв’язок між змінними двоїстих моделей.
Третя теорема двоїстості. Її економічний зміст. Поняття цінності ресурсу, та його використання в економічному аналізі задач.
Транспортна модель.
Лінійні цілочисельні задачі.
Задачі нелінійного програмування.
Поняття економетричного моделювання. Зв’язок економетрії з іншими науками. Етапи економетричного моделювання.
Парна регресія. Оцінка лінійної залежності двох змінних.
Класична лінійна модель множинної регресії.
Оцінка якості регресійної моделі та статистична значущість коефіцієнтів регресії.
Питання-визначення:
Постановка задачі лінійного програмування
Визначення області допустимих розв’язків ЗЛП.
Який розв’язок ЗЛП називається допустимим розв’язком
Визначення опорного розв’язку ЗЛП
Визначення оптимального розв’язку ЗЛП
Визначення поняття – альтернативний розв’язок
Який розв’язок називається необмеженим
Дайте формулювання правила симплексних перетворень як мнемонічного правила прямокутника
Сутність аналізу моделей на чутливість
Дайте визначення поняття дефіцитний ресурс
Дайте визначення поняття недефіцитний ресурс
Визначення поняття цінність ресурсу
Визначення поняття інтервал стійкості двоїстих оцінок
Постановка транспортної задачі
Визначення опорного плану транспортної задачі
Визначення оптимального плану перевезень транспортної задачі
Формулювання правила методу північно-західного кута
Формулювання правила методу мінімального елемента
Постановка задачі лінійного цілочисельного програмування
Постановка задачі нелінійного програмування.
Визначення економетрії
Постановка задачі регресійного аналізу
Поняття коефіцієнта коваріації
Поняття коефіцієнта кореляції
Поняття коефіцієнта детермінації
1. Основні аспекти математичного моделювання економіки.
Невозможно представить себе современную науку без широкого применения мат. моделирования. Сущность моделир. состоит в замене исходного объекта его упрощенным образом (мат. моделью) и дальнейшее изучение модели с помощью мощного мат. аппарата с применением вычислительных алгоритмов реализуемых на компьютерах.
Во многих практических ситуациях необходимо решить задачу о том, как лучшим образом организовать некоторое мероприятие (провести операцию), чтобы достичь определенной цели. Решение может быть принято интуитивно, на основе жизненного опыта, но чем сложнее, дороже и масштабнее операция, тем более предпочтительными будут научные мат. методы, которые позволяют заранее оценить последствия каждого решения и обосновать выбор такого решения, которое будем считать наилучшим.
Мат. моделир. – это абстракция реальной действительности, в которой соотношение между реальными элементами объекта описанных с помощью соотношений между мат. категориями (с помощью известных мат. операций).
Модель – упрощенный образ реального объекта, который в процессе изучения данного объекта заменяет реальный.
Работа не с самим объектом (явлением, процессом), а с его моделью дает возможность безболезненно, относительно быстро и без существенных затрат исследовать свойства и поведение объекта в любых мысленных ситуациях. Мат моделирование не заменяет собой другие научные способы изучения, а является 1 из способов познания.
Моделирование присутствует практически во всех видах деятельности людей (транспортная задача, задача о назначении, управление запасами, моделирование в маркетинге (определение цены товара, задачи распределения реального бюджета и т.д.), задача библиотечного обслуживания и т.п.)
Мат моделирование приносит хорошие результаты при выполнении хорошо известных проф. требований (четкая формулировка постановки задачи, подробное описание объекта или явления, точность вычислительных алгоритмов, четкое определение целей исследования, выделение исследователем известных и неизвестных параметров и т.д.).
2. Задача лінійного програмування. Постановка. Геометрична інтерпретація (загальна). Методи розв’язання.
3. Геометрична інтерпретація задачі лінійного програмування (детальна).
ЗЛП
В даннях разделе рассматривается самый простой тип задач – ЗЛП. В моделях таких задач используются детерминированные данные (статические, а не динамические) и лин. ф-ции для описания взаимосвязей между переменными.
Общая модель ЗЛП может быть записана так:
Сокращенная форма модели такая:
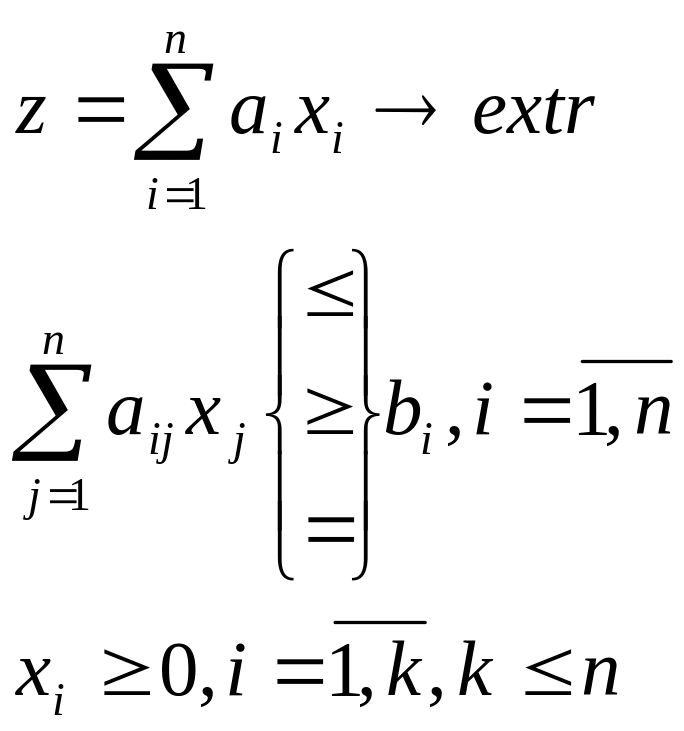
Существует 3 вида оптимизационных моделей:
1) общая:
,
ограничения – любые, условия неотр. –
необязательны
2) каноническая
,
ограничения – равенства, УО – обязательны
3) стандартная
,
ограничения (
),
УО – необязательны
Различные формы моделей необходимы для того, чтобы можно было принять разные методы решения. Задачу можно преобразовать от 1 формы к другой при помощи определенных правил.
Геометрическая интерпретация
Гр. интерпретация возможна для ЗЛП, модель которой содержит 2, максимум 3 переменные. Для задач большей размерности геом. интерп. дается обобщением полученных свойств.
Для 2 переменных:
Ограничения задачи тогда в общем виде записывается такой с-мой:
Ограничения-равенства – равенство с 2 переменными, можно построить по 2 точкам.
Ограничения-неравенства – полуплоскость, которая отображается соотв. прямой и может быть определена, например методом контрольной точки. Если с-ма совместна, то пересечение полуплоскостей образует некоторую общую область, которая называется ОДР задачи, каждая точка этой области может быть решением задачи.
ОДР может быть многоугольникам, отрезком, точкой, а так же неограниченной многоугольной областью.
Имеет место такое свойство ОДР: если любые 2 точки ОДР ЗЛП соединить отрезком, то но будет полностью лежать в данном множестве. Такие множества называются выпуклыми.
Для 3 переменных:
Ограничения – полупространства, полученное относительно ограничений плоскости. Пересечение всех плоскостей и полупространств позволяет определить выпуклый многогранник, который представляет собой ОДР задачи.
Если больше 3 переменных:
Каждое ограничение-равенство – гиперплоскость, а ограничение-неравенство – полупространство. Если с-ма совместна, то аналогично с рассм. выше случаями пересечение всех множеств образует многогранник допустимых решений.
Интерпретация цф
ЦФ ЗЛП геометрически
представляют множеством линий уровня,
которые задаются уравнением:
Для n=2
линии уровня имеют вид
и
представляют собой семейство параллельных
прямых , каждой из которых соотв.
определенное значение цф
ЦФ при n=3
гр. представляется линиями уровня
,
которые задают семейство параллельных
плоскостей.
При n=4 линии уровня цф образуют семейство параллельных гиперплоскостей.
Линии уровня заполняют все пространство, чес больше значений const, тем выше (или ниже) соотв. линии уровня. И следовательно больше (меньше) значение цф.
Решение ЗЛП состоит в том, чтобы найти такую точку ОДР, в которой цф будет достигать наибольшего или наименьшего значения.
Используя гр. интерпретацию задачи процесс поиска опт. решения может быть осуществлен такими этапами:
1) по огр. задачи строится ОДР
2) строятся линии
уровня цф, которые задаются так:
3) определяется направление возрастания (убывания) цф
4) Передвигаются линии уровня в направлении возрастания, определяют точку минимума как первую точку касания линии уровня и ОДР и точку максимума как последнюю.
Частные случаи решения:
1) альтернативное решение – такое решение, при котором цф достигает макс или мин значения не в 1 точке, а на целом множестве точек. Решение получаем в виде отрезка, ограниченного двумя вершинами многогранника и ответ записываем в виде:
2) неограниченное
решение – возможно при неограниченном
ОДР (
)
Замечание: при неограниченной ОДР цф не всегда неограниченна, может существовать конечный макс.
Теорема: Если ЗЛП имеет опт. решение, то цф достигает своего экстремального значения в 1 из вершин ОДР (многоугольник).