6) Двоїстість у лінійному програмуванні. Структура та властивості двоїстих задач.

С каждой задачей лин.программирования связана др. лин.задача, называемая двойственной. Взаимосвязь прямой и двойственной задач заключается в том, что решение одной задачи может быть получено из решения другой. Кроме того, рассмотрение двойственных задач играет большую роль в эк.анализе моделей. Построение двойственных задач. Первоначальная задача – распределение ограниченной продукции. Пусть фирма имеет m видов ресурсов S1, S2, S3 … Sm, которые имеются в запасе b1, b2 … bm соответственно. Фирма производит n видов продукции Х1, Х2 … Хn, известны цены реализации единицы каждого изделия С1, С2 … Сn. Также известны нормы затрат ресурсов на производство каждой продукции. Они задаются технологической матрицей, 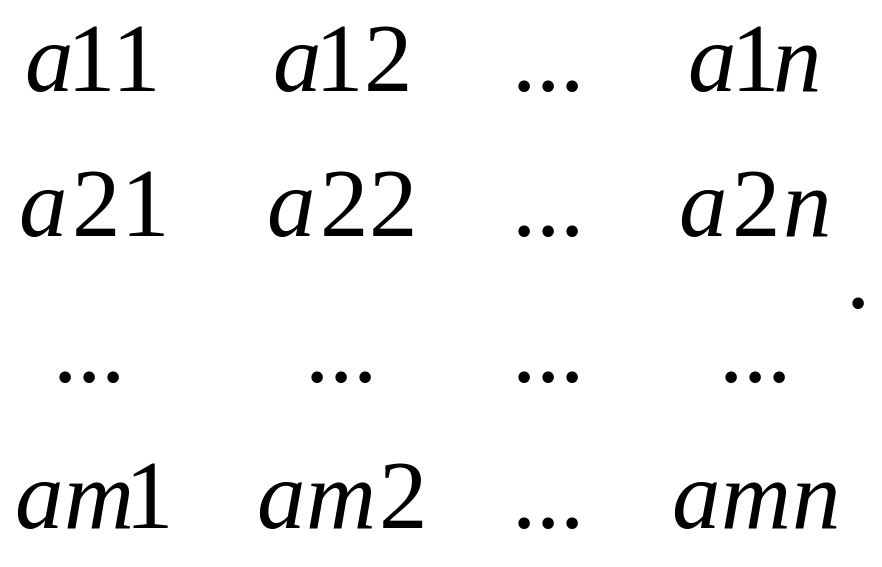где aij – затраты i-го ресурса на производство j-продукции. Требуется составить план выпуска продукции, максимизирующей доход от реализации изделий. Построим мат.модель этой задачи: 1. Xi – объём производства i-продукции, i = 1, 2 … n.

2. Z = C1X1 + C2X2 + … + CnXn max – максимизация дохода.

3. Ограничения на запасы ресурсов:

a 11X1 + a12X2 + … +a1nXn <= b1;

a21X1 + a22X2 + … +a2nXn <= b2;

…

am1X1 + am2X2 + … +amnXn <= bm.

X1, X2 … Xn >= 0.

Решением данной модели будет оптимальный план выпуска продукции X*=(X1*, X2*…Xn*), который обеспечивает доход.

Двойственную задачу получим из следующих соображений: предположим, что при определённых условиях ресурсы выгодно продать, поэтому нужно определить оптимальные цены ресурсов. Строим мат.модель данной задачи:

1. Yi – оценка стоимости i-ресурса, i=1, 2…m.

2. ЦФ определяет интересы покупателя. Стоимость всех ресурсов должна быть минимальной. F=b1Y1 + b2Y2 + … + bmYm min.

3. Ограничения составляются исходя из интересов продавца. С точки зрения продающей стороны выручка, полученная от продажи ресурсов должна быть не меньше той суммы, которую фирма может получить при переработке имеющихся ресурсов в готовую продукцию и её реализацию. Составляются ограничения по каждому изделию:

a 11Y1 + a21Y2 + … +am1Ym <= C1;

a12Y1 + a22Y2 + … +am2Ym <= C2;

…

a1nY1 + a2nY2 + … +amnYm <= Cn.

Y1, Y2 … Ym >= 0.

Решением данной модели будут оптимальные стоимости всех ресурсов Y*=(Y1*, Y2*…Ym*). Построенная пара задач является парой двойственных задач. Если проанализировать их модели, то можно выявить следующие закономерности: 1) Если ЦФ исходной задачи направлена на max, то двойственной – на min, и наоборот; 2) Коэффициенты ЦФ исходной задачи становятся правыми частями ограничений двойственной, и наоборот; 3) Число переменных исходной задачи равно числу ограничений двойственной, и наоборот число ограничений исходной равно количеству переменных в двойственной; 4) Матрица ограничений двойственной задачи получается транспонированием исходной матрицы ограничений.

Кроме этих общих закономерностей существуют ещё такие правила построения двойственных задач: 1) Перед построением двойственной задачи модель исходной упорядочивается, т.е.: max(<=,=); min(>=,=). 2) Каждой переменной исходной задачи соответствует ограничение двойственной. Если на i-переменную исходной задачи наложено условие неотрицательности, то соответствующее ограничение двойственной модели будет неравенством, в противном случае равенством. 3) Каждому ограничению исходной задачи соответствует переменная двойственной. Если j-ограничение исходной модели – неравенство, то на j-переменную двойственной задачи будет накладываться условие неотрицательности. В противном случае – не будет.