2.3. Інтегрування по частинам

Якщо функції та неперервні разом зі своїми похідними на , то

(2.8)

Цю формулу називають формулою інтегрування по частинам. Вона залишається справедливою і для випадку, якщо замість неперервності похідних і вимагається лише інтегровність.

1. Знайти інтеграл Оскільки то

2. Знайти інтеграл

Знайшовши з одержаного рівняння значення , одержимо

3. Обчислити Проводячи інтегрування по частинам маємо звідки За допомогою знайденої рекурентної формули можливо одержати остаточний результат для будь-якого натурального .

Нехай тоді оскільки

Нехай тоді оскільки

Таким чином, (2.9)

Зауважимо, що формула справедлива і для

В деяких випадках доцільно комбінувати метод заміни змінної з методом інтегрування по частинам.

4. Знайти інтеграл . Застосовуючи формулу (2.8) , одержимо інтеграл Зробивши в ньому заміну одержимо інтеграл . Наведемо відповідь:

2.4. Обчислення площ плоских фігур

Н ехай функція неперервна і невід’ємна на сегменті . Площа фігури (мал. 2.1), обмеженої графіком функції відрізком осі і відповідними відрізками прямих та дорівнює

(2.10)

Фігуру називають криволінійною трапецією.

Функція може бути задана параметричними рівняннями , де функція має неперервну невід’ємну похідну на , а функція неперервна і невід’ємна на , тоді площа фігури обчислюється по формулі: (2.11)

Н ехай задана функція , де неперервна і невід’ємна на . Площа сектора (мал. 2.2), обмеженого графіком функції в полярних координатах і відповідними відрізками променів і , обчислюється за формулою:

(2.12)

Знайти площі фігур, обмежених кривими.

1. Побудуємо криві, які обмежують фігуру (мал. 2.3). Знайдемо абсцису точки перетину тангенсоїди і косинусоїди: Звідси маємо рівняння Оскільки одержимо Враховуючи, що , маємо ,

(кв. од.)

2 .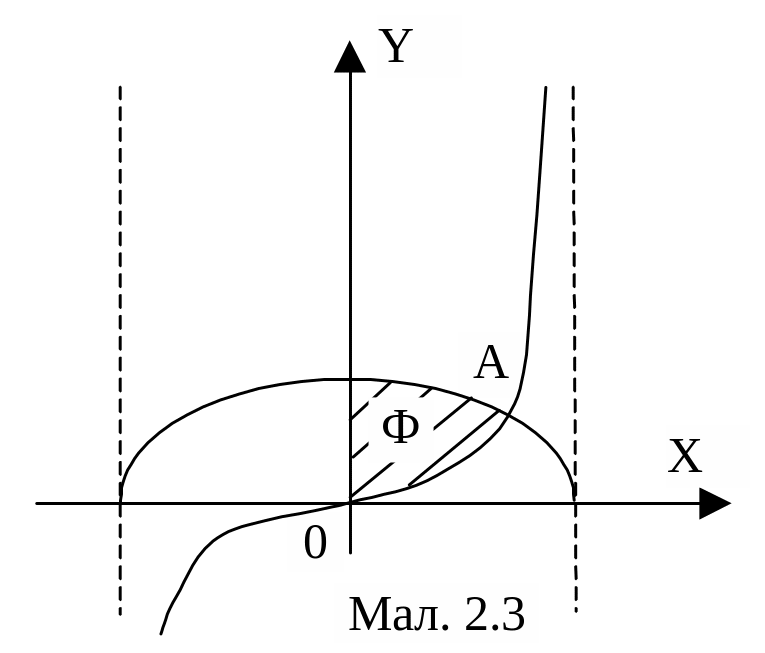

П обудуємо криві, які обмежують фігуру (мал. 2.4). Розв’язавши систему рівнянь знайдемо точки перетину параболи та прямої: (0;-1) і (4;3). . Враховуючи, що фігура симетрична відносно осі ОХ, її площу знайдемо як . Площу фігури знайдемо як Тут враховано, що довільна пряма, проведена знизу вгору паралельно осі має точку входу на прямій а точку виходу – на додатній гілці параболи Маємо:

(кв.од.)

3.

Для побудови кривої, яка обмежує фігуру , приймемо до уваги, що звідки Тоді звідки Точки перетину кривої (а вона симетрична відносно осі ) знайдемо з умови . Маємо Врахуємо, що отже, Спочатку крива попаде в точку (0;0), потім у точку і, утворивши п етлю, знову в точку (0;0) – точку саме перетину кривої. Оскільки то в початковій точці (0;0) в кінцевій точці половини петлі (мал.2.5) По формулі (2.11):

4.

П ерейдемо до полярних координат і , поклавши Рівняння кривої буде мати вигляд , звідки (крива двічі виходить і виходить в полюс) і Оскільки (маємо на увазі ), то звідки З умови зрозуміло, що отже, крива розміщена в І і ІІІ чвертях симетрично і відносно початку координат, і відносно бісектриси Зауважимо, що найбільше значення буде мати при Враховуючи сказане, будуємо дану криву (мал. 2.6). Площу фігури знайдемо по формулі (2.12):