(2.1)

який назвемо інтегральною сумою. Якщо існує скінчена границя яка не залежить від способу розбиття сегмента і вибору точок то число називають означеним інтегралом функції на сегменті і позначають символом

(2.1)

а функцію називають інтегрованою по Ріману на цьому сегменті.

2.1.2. Нижня та верхня інтегральні суми Дарбу

Нижньою та верхньою сумами Дарбу функції на сегменті при фіксованому розбитті цього сегмента, називають відповідно суми

(2.3)

де

2.1.3. Критерій інтегровності

Для того, щоб функція була інтегровною на сегменті необхідно і достатньо, щоб виконувалась рівність

(2.4)

де коливання функції на сегменті . Зокрема неперервна функція, кусочно-неперервна функція і монотонна на сегменті інтегровні на ньому.

1.Обчислити, виходячи з означення, інтеграл

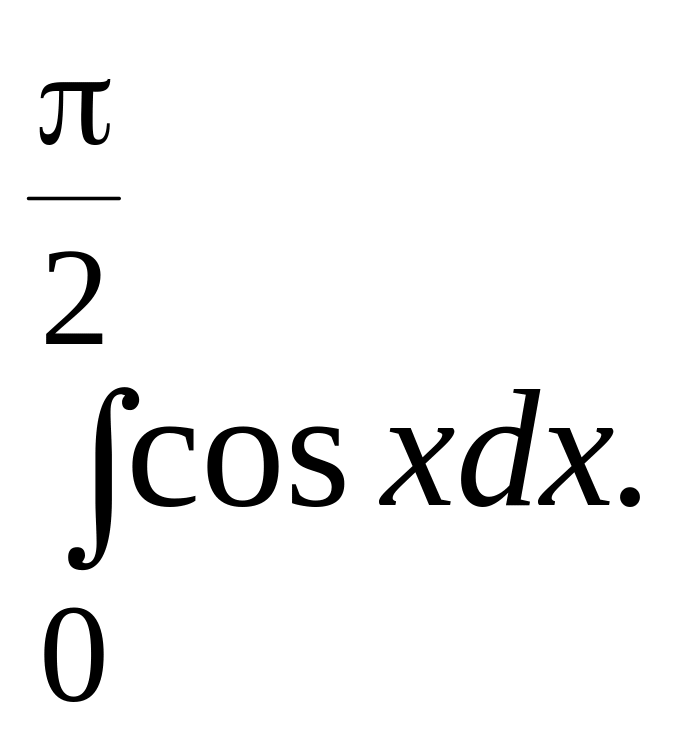
Розіб’ємо сегмент на рівних частин точками Довжина кожного частинного сегмента дорівнює За виберемо правий кінець го частинного сегмента. Обчислимо значення функції в точках : Складемо інтегральну суму . Методом математичної індукції можна показати, що 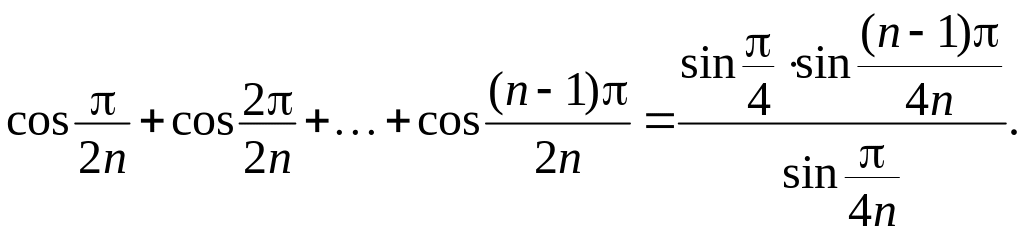Оскільки то .

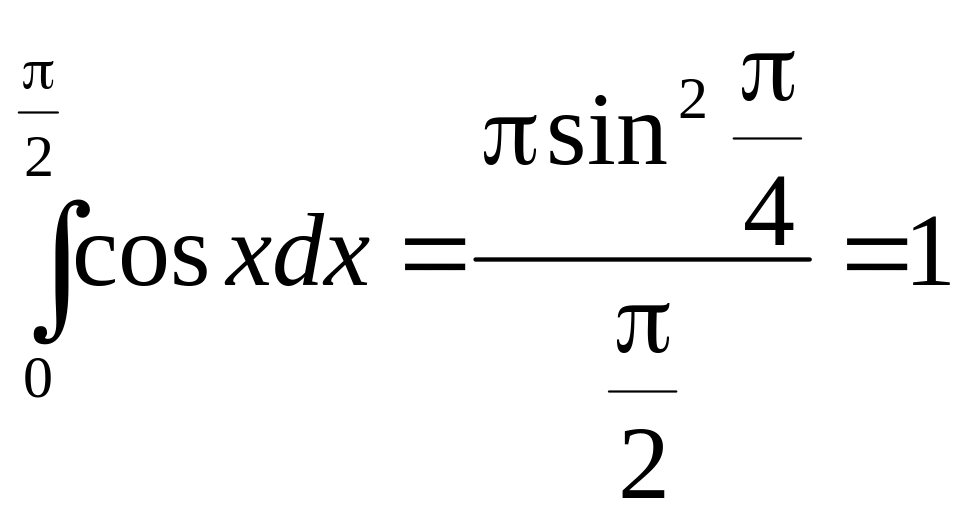В деяких випадках розбивають сегмент інтегрування на нерівні частини.

2. Обчислити, виходячи з означення, інтеграл

Покладемо та розіб’ємо сегмент на частини точками де На сегменті виберемо точку Тоді Звідси згідно формули для суми геометричної прогресії:

.

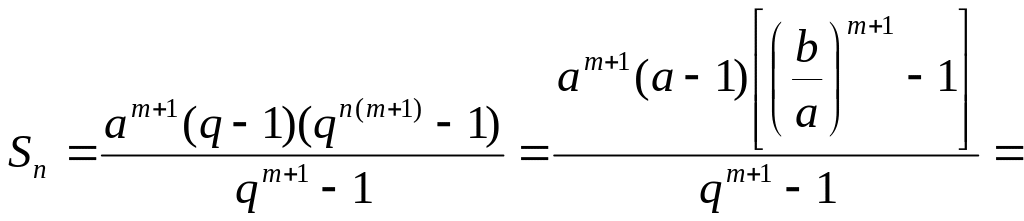
Якщо а отже, то Отже, . Тому Ця формула вірна при .

2.1.4. Властивості інтегралу

1)

2) Якщо функція інтегрована на сегменті то вона інтегрована на будь-якому сегменті .

3) Адитивність інтегралу

4) Лінійність інтегралу .

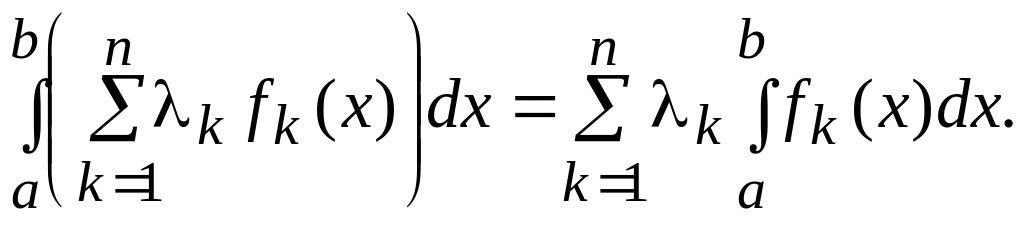5) Добуток інтегровних на сегменті функцій інтегровний на ньому.

6) Якщо функція інтегровна на сегменті і то функція також інтегровна на цьому сегменті.

7) Якщо функції і інтегровані на сегменті і то Зокрема, якщо на сегменті функція то

8) Якщо функція інтегровна на сегменті , то і її абсолютна величина також інтегровна на і

9) Неперервність інтегралу. Якщо функція інтегровна на сегменті , то функція та неперервні на цьому сегменті.

3. Оцініть інтеграл

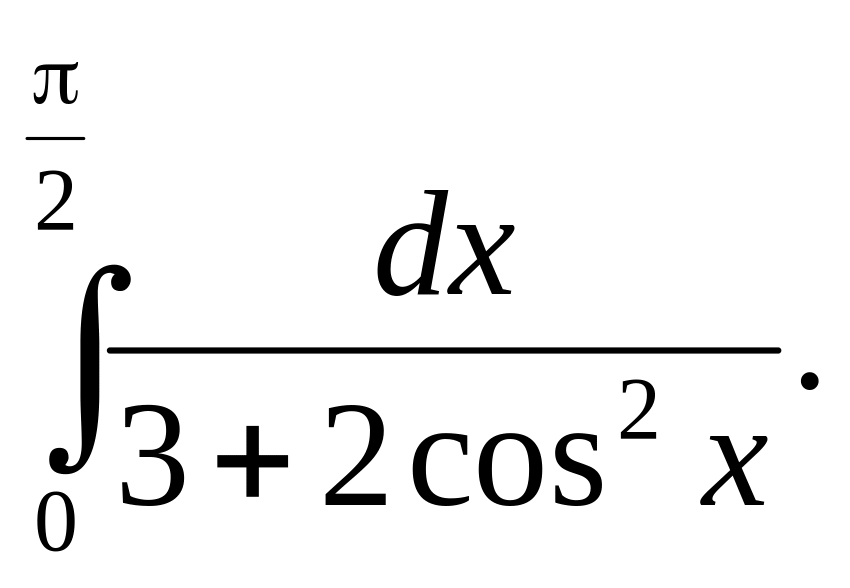
Оскільки то та

4. Довести, що якщо функція інтегровна та невід’ємна на сегменті , а функція задовольняє на цьому сегменті умові причому інтегровна, то

(2.5)

Із умови випливає, що при виконується нерівність Інтегруючи цю нерівність, приходимо до співвідношення (2.5).

Застосуємо (2.5) для оцінки інтегралу Покладемо Оскільки на сегменті маємо то і тому

2.1.5. Формула Ньютона-Лейбніца

Якщо функція неперервна на сегменті то для будь-якої її первісної має місце формула Ньютона-Лейбніца

(2.6)

5. Обчислити

6. Чи можна застосувати формулу Ньютона-Лейбніца до інтегралу ?

Відповідь негативна. Якщо формально обчислити цей інтеграл по формулі (2.6), то одержимо Невірний результат: Але підінтегральна функція і по властивості 7) інтеграл не може бути від’ємним числом. Застосування формули Ньютона-Лейбніца незаконне, оскільки має нескінчений розрив в точці , яка належить проміжку інтегрування.

2.2. Формула заміни змінної

Якщо функція неперервна на сегменті , а функція неперервна та диференційована на сегменті , то

(2.7)

1. .

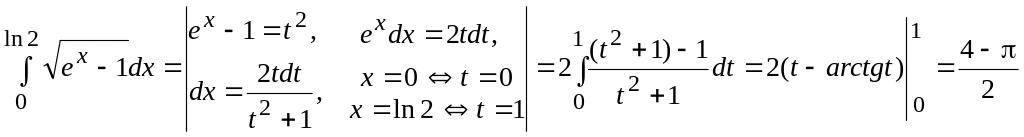2. Обчислити інтеграл за допомогою заміни Покладемо При при Отже, Але Помилка тут полягає в тому, що функція має дві обернені функції: і . Якщо взяти то але не -1, як вимагає умова; якщо ж взяти то але не +2, як вимагає цього умова. Тоді необхідно розбити інтеграл: і в першому інтегралі покласти а в другому Таким чином,

3. Довести, що якщо неперервна на , то

Запишемо і покладемо Одержимо Тоді .

Застосуємо доведену рівність для обчислення інтегралу

Маємо .