1.5.4. Інтеграл виду

(1.13)

де многочлен степеня як правило, не виражаються через елементарні функції і в цьому випадку при і називаються еліптичними, а при гіпереліптичними. В цьому випадку, коли інтеграл (1.13) при і є елементарною функцією, він називається псевдоеліптичним. Кожний еліптичний інтеграл може бути виражений через елементарні функції і через стандартні еліптичні інтеграли:

(1.14) (1.15)

(1.16)

Заміною ці інтеграли зводяться до лінійних комбінацій інтегралів:

(1.17) (1.18)

(1.19)

які називають відповідно еліптичними інтегралами першого, другого, третього роду в формі Лежандра.

Через та позначимо відповідно ту з первісних (1.17) і (1.18), яка при перетворюється в нуль.

1.

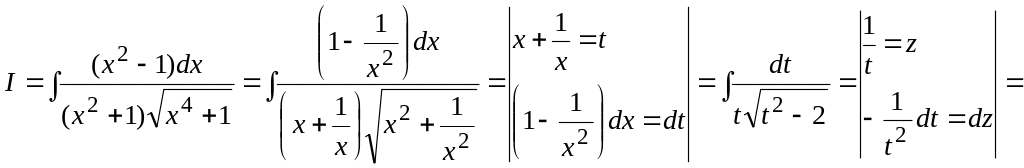
2.

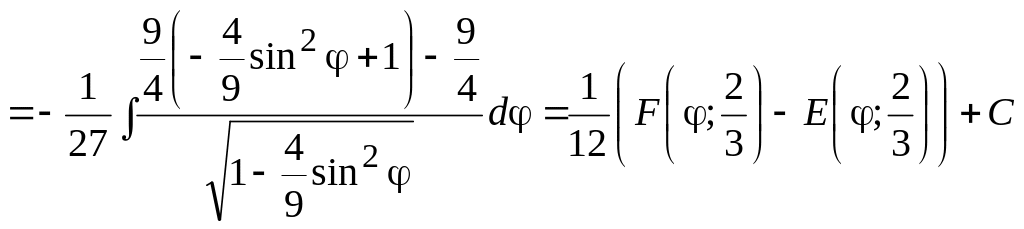, де

1.6. Інтегрування трансцендентних функцій

1.6.1. Інтеграли виду

(1.20)

де раціональна функція змінних і завжди можна звести до інтегралів від раціональних функцій за допомогою підстановки (її називають універсальною тригонометричною підстановкою)

(1.21)

Ця підстановка перетворює інтеграл (1.20) до виду: (1.22)

Помітимо, що підстановка (1.21) часто призводить до громіздких викладок, тому її використовують тоді, коли не знайдено інших шляхів інтегрування.

1.

Якщо підінтегральна функція має одну із властивостей:

1)

2)

3)

то для обчислення інтегралу зручно використовувати відповідні підстановки:

1) 2) 3)

2. Тут тому, поклавши

В деяких випадках обчислення інтегралу (1.20) досягається застосуванням інших прийомів.

3.

4. Скористаємося тотожністю .

.

1.6.2. Інтеграли виду

(1.23)

де раціональна функція зміних і , завжди можна звести до інтегралів від раціональних функцій з допомогою підстановки Іноді зручно використовувати підстановки

5. .

6. Представимо чисельник підінтегральної функції у вигляді лінійної комбінації знаменника і похідної знаменника: . Для і одержимо систему рівнянь: звідки

1.6.3. Інтеграли виду

(1.24)

підстановками або і відповідно або завжди можна звести до інтегралів від диференціального бінома.

7. . Покладемо тоді

8. Часто рекомендують в цьому випадку зробити підстановку . Доцільно понизити степінь косинуса:

Зауважимо, що при досить великих зручно застосовувати формули зниження (які одержують інтегруванням по частинам):

9.

1.6.4. Інтеграли виду

(1.25)

обчислюються після перетворення добутку тригонометричних функцій в алгебраїчну суму за допомогою відомих формул тригонометрії:

10. .

Тоді

1.6.5. Інтеграли виду

(1.27)

де многочлен степеня а одна з наступних функцій: обчислюються за допомогою багатократного інтегрування по частинам. Методами інтегрування по частинам і заміни змінної інтегруються і інші трансцендентні функції (див. підр. 1.2, 1.3).

11.

12. . Рахуючи інтеграл двічі по частинам,

Зауважимо, що має місце формула Ейлера:

яку можна використати для контролю при обчисленні відповідних інтегралів.

13. Нехай , Інтегруючи раціональний дріб (див. підрозд. 1.4) та повертаючись до змінної , одержимо Форма відповіді підказує, що даний інтеграл можна було б звести до інтегралу Дійсно,

14. . Будемо шукати відповідь у вигляді:

(обидва многочлени беремо другого степеня, хоча коефіцієнт при многочлен першого степеня). Після диференціювання одержуємо:

Одержимо і