1.5. Інтегрування ірраціональних функцій

Часто зустрічаються інтеграли від ірраціональних функцій, які можна обчислити методом раціоналізації підінтегральної функції. Він полягає в тому, що підшукується заміна змінної, яка перетворює інтеграл від ірраціональної функції в інтеграл від раціональної функції.

1.5.1. Інтеграл виду

(1.5)

де , заміною ( – спільний знаменник чисел ) приводиться до інтегралу від раціональної функції.

1. Зробимо заміну тоді .

Підінтегральну функцію представимо у виді

В задачах підрозд. 1.4 приділено достатньо уваги інтегруванню раціональних дробів, тому обмежимося наведенням відповіді

.

1.5.2. Інтеграл виду

(1.6)

зводиться до інтегралів від раціональної функції підстановками Ейлера:

якщо а>0;

якщо с>0;

де один із коренів квадратного тричлена.

1. Скористаємося першою підстановкою Ейлера, поклавши Після піднесення до квадрату одержимо: , .

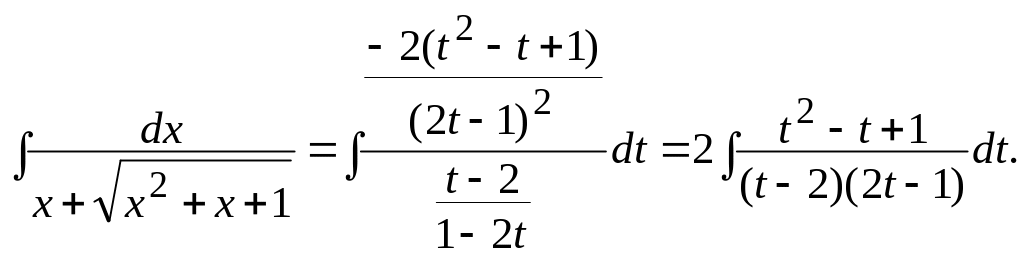Для підінтегральної функції маємо:

де

Зауважимо, що підстановки Ейлера часто призводять до громіздких викладок. Інтеграли виду (1.6) можна звести до інтегралів типу

(1.7) (1.8)

<0 (1.9)

Для обчислення інтегралу (1.7) зручно користуватися формулою Чебишева

(1.10)

де многочлен з неозначеними коефіцієнтами; неозначений коефіцієнт. Покажемо це на прикладі 3.

3. Скористаємося формулою (1.10). Обчислимо похідні по :

, .

Тоді .

Інтеграл (1.8) заміною приводиться до інтегралу (1.7). Покажемо на прикладі 4, як береться інтеграл виду (1.9).

4. Нехай де і підберемо так, щоб в квадратних тричленах і (1.9) зникли члени, які мають :

маємо систему рівнянь звідки Візьмемо: (не має значення, який розв’язок системи взяти). Тоді , При а отже, маємо .

У першому інтегралі покладемо тоді він дорівнює: У другому інтегралі зробимо заміну Абеля: Тоді Другий інтеграл буде мати вигляд: Повертаючись до змінної остаточно одержимо:

1.5.3. Інтеграли виду

(1.11)

де при цьому називають інтегралами від диференціального бінома. Ці інтеграли зводяться до інтегралів від раціональних функцій тільки в трьох випадках (теорема Чебишева):

(1.12)

У випадку 1) застосовується заміна де спільний знаменник дробів і , у другому і третьому випадках ― відповідно заміни та де – знаменник дробу

5. . Перепишемо інтеграл у вигляді . У нас Маємо третій випадок диференційного бінома, оскільки ціле число. Згідно з теоремою Чебишева, застосуємо заміну тобто Тоді Продиференціювавши обидві частини підстановки, одержимо: Не знаходячи зразу ж переходимо до інтегралу (підстановка забезпечує зникнення змінної !): тоді Одержали інтеграл від раціонального дробу. Враховуючи, що знайдемо неозначені коефіцієнти у розкладі і знайдемо значення інтегралу. Наведемо відповідь для самоконтролю: де

6. Тут Оскільки ціле число, то заданий інтеграл заміною зводиться до інтегралу від раціональної функції змінної . Знаходимо

.