Порядок выполнения работы

1. Вычислить корни полиномов:

2. Построить графики этих функций, умножить полиномы, определить корни результирующего полинома и восстановить коэффициенты полиномов.

3. Продифференцировать исходные полиномы и определить их корни.

4. Для экспериментальных данных, заданных таблично, выбрать аппроксимирующий полином и определить его коэффициенты. Восстановить значение полинома в узлах интерполяции. Построить графики исходной зависимости и аппроксимирующего полинома.

х	15	29	41	50	59	72	80	91
у	3.3	6.3	6.87	7.4	8.1	8.43	8.8	9.24

Вопросы для самопроверки

1. Каким образом нужно задавать полиномы, чтобы выполнять с ними алгебраические операции сложения, умножения и деления?

2. С помощью каких операторов можно вычислить корни полинома, восстановить его коэффициенты и построить график?

3. Что такое интерполяция и аппроксимация экспериментальных данных?

4. Как выбирается порядок аппроксимирующего полинома и с помощью какого оператора можно выполнить полиноминальную аппроксимацию?

Литература

1. С. В. Поршнев MATLAB 7. Основы работы и программирования. Учебник – М.: ООО <<Бином-Пресс>>, 2006г. -320 с.: ил.

2. Курбатов Е.А. MATLAB 7. Самоучитель. – М.: Издательский дом “Вильямс”, 2006. – 256 с.: ил.

3. Половко А.М., Бутусов П.Н. MATLAB для студента. – СПб.: БХВ-Петербург, 2005. – 320 с.: ил.

4. В.П. Дьяконов MATLAB 6.5 SP1/7 + Simulink 5/6. Основы применения. Серия << Библиотека профессионала >>.-М.: СОЛОН-пресс, 2005. -800 с.: ил

5. Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9 /Алексеев Е.Р., Чеснокова О.В. – М.: НТ Пресс, 2006. – 496с. : ил.

Лабораторная работа № 5 Решение обыкновенных дифференциальных уравнений и систем обыкновенных дифференциальных уравнений

Цель работы: изучить встроенные функции для решения обыкновенных дифференциальных уравнений; решение дифференциальных уравнений в среде Simulink.

Введение

Под обыкновенным дифференциальным уравнением понимают уравнение, содержащее аргумент, искомую функцию этого аргумента и её производные различных порядков. Решением или интегралом дифференциального уравнения является функция, удовлетворяющая ему – подстановка этой функции и её производных превращает дифференциальное уравнение в тождество. Дифференциальное уравнение рассматривается как математическая модель физических процессов, происходящих в электрических цепях и объектах управления. Например, для последовательного соединения индуктивности L и резистивного элемента R справедливо следующее дифференциальное уравнение

(1)

где i – ток, e(t) – эдс источника. Решение таких уравнений можно проводить классическим, операторным и численным методом, а также методом переменных состояния.

Для решения линейного дифференциального уравнения n-го порядка можно применять прямое и обратное преобразование Лапласа. Применяя прямое преобразование Лапласа к дифференциальному уравнению, получим

Если R =10 Ом, L = 0,1Гн, Е = 100 В, то

Для получения решения исходного дифференциального уравнения необходимо применить обратное преобразование Лапласа. В MATLAB предусмотрена функция iLaplace(L,t) для нахождения обратного преобразования Лапласа. Здесь L – прямое преобразование Лапласа искомой функции, а t – аргумент искомой функции. Предварительно необходимо создать группу символьных объектов с помощью функции syms:

>> syms s t I;

>> I=100/(s*(0.1*s+10));

>> i=iLaplace(I,t)

i =

10-10*exp(-100*t)

Следовательно, i(t)=10 – 10 e^{-100 t}.

Дифференциальные уравнения можно решать в среде Simulink пакета MATLAB. Для этого надо создать новую модель для решения дифференциального уравнения, используя блоки интеграторов, сумматоров, усилителей, осциллографов, сигналов и передаточных функций непрерывных систем. Структурные схемы решений дифференциального уравнения первого порядка (1) приведены на рис. 1.

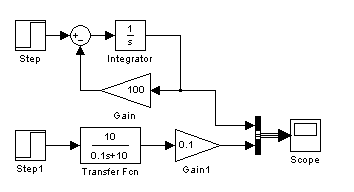
Рис. 1

Для решения обыкновенных дифференциальных уравнений и систем обыкновенных дифференциальных уравнений первого порядка в MATLAB используется функция dsolve(…).

Рассмотрим решение уравнения

при начальных условиях y(0)=0 :

>> x=dsolve('0.1*(Dx)+10*x=100','x(0)=0')

x =

10-10*exp(-100*t).

Мы получили такое же решение, что и в предыдущем случае.

Рассмотрим решение уравнения

(2)

при начальных условиях y(0)=0 и dy/dt(0)=-4:

>> x=dsolve('(D2x)+2*(Dx)+5*x=0','x(0)=0','Dx(0)=-4')

x =

-2*exp(-t)*sin(2*t)

Дифференциальное уравнение второго порядка (2) путём подстановки y1=y и y2=dy1/dt можно свести к системе двух дифференциальных уравнений первого порядка:

Для численного решения этой системы уравнений необходимо создать m-функцию для вычисления правых частей этой системы уравнений:

function F=md(t,y)

F=[y(2);-5*y(1)-2*y(2)];

Её необходимо сохранить в m-файле под именем md в папке work. Аргумент функции md время t, по которому проводится дифференцирование и вектор Y, размерность которого определяется числом неизвестных функций системы дифференциальных уравнений первого порядка.

Для решения систем обыкновенных дифференциальных уравнений первого порядка в MATLAB имеются встроенные фукции (решатели): ode23, ode45, de113, ode15s, ode23s,ode23t и ode23tb. Они реализуют различные численные методы решения дифференциальных уравнений – Рунге - Кутты, Адамса – Башворта – Мултона, Розенброка, метод трапеций и методы переменного порядка.

В качестве решателя выбираем функцию ode45(‘f’,[t0 tk],[y0]), где f – имя m-файла, в котором содержатся правые части системы дифференциальных уравнений; t0, tk – начальное и конечное значения аргумента; y0 – вектор-столбец начальных условий. Эта функция используется для решения нежёстких систем дифференциальных уравнений:

>> [t,Y]=ode45('md',[0 5],[0;-4]);

Графики решения можно получить с помощью операторов

>> plot(t,Y(:,1),'o',t,Y(:,2),'x') - (рис. 2)

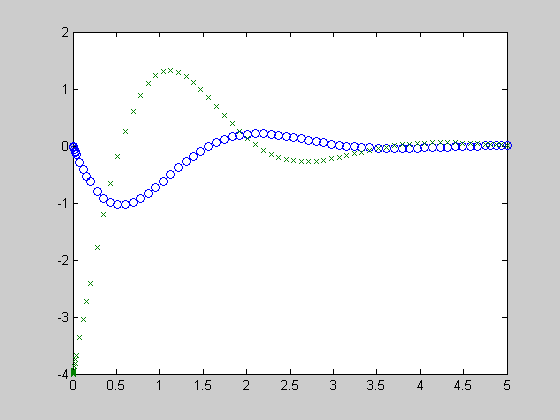
Рис. 2

>> plot(t,Y) – (рис. 3)

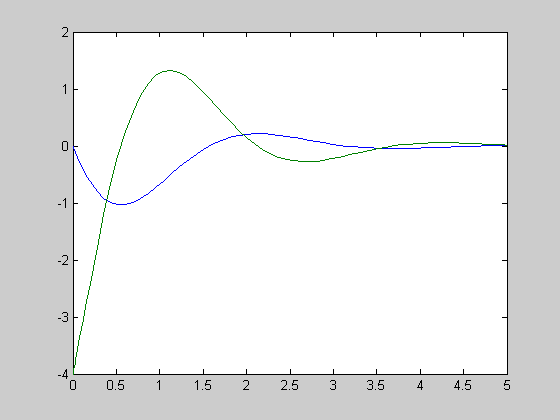
Рис. 3

или вывести таблицу (если убрать ;).

Порядок выполнения работы

1. Найти решение следующих линейных дифференциальных уравнений

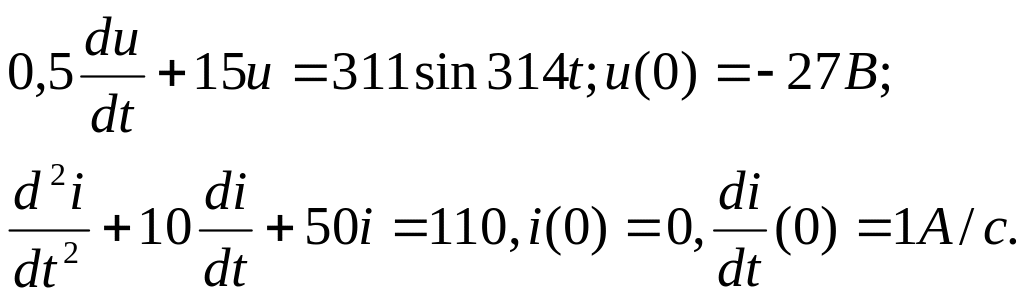
всеми рассмотренными методами и построить графики решений.

2. Найти решение дифференциального уравнения второго порядка

,

предварительно преобразовав его к системе двух дифференциальных уравнений первого порядка.

Вопросы для самопроверки

1. Какие решатели предусмотрены в MATLAB для решения обыкновенных дифференциальных уравнений? Зависит ли выбор той или иной функции от характеристики решаемой задачи?

2. В чём состоит преимущество преобразования Лапласа перед другими методами решения дифференциальных уравнений?

3. С помощью каких функциональных блоков решаются дифференциальные уравнения в MATLAB + Simulink?

Литература

1. С. В. Поршнев MATLAB 7. Основы работы и программирования. Учебник – М.: ООО <<Бином-Пресс>>, 2006г. -320 с.: ил.

2. Курбатов Е.А. MATLAB 7. Самоучитель. – М.: Издательский дом “Вильямс”, 2006. – 256 с.: ил.

3. Половко А.М., Бутусов П.Н. MATLAB для студента. – СПб.: БХВ-Петербург, 2005. – 320 с.: ил.

4. В.П. Дьяконов MATLAB 6.5 SP1/7 + Simulink 5/6. Основы применения. Серия << Библиотека профессионала >>.-М.: СОЛОН-пресс, 2005. -800 с.: ил

5. Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9 /Алексеев Е.Р., Чеснокова О.В. – М.: НТ Пресс, 2006. – 496с. : ил.

Лабораторная работа № 6 Математическое моделирование

Цель работы: изучить методы решения систем линейных алгебраических уравнений.