Лабораторная работа № 10 Обработка экспериментальных данных и аппроксимация характеристик нелинейных элементов
Цель работы: изучить методы обработки данных
Введение
При анализе нелинейных электрических цепей возникает задача обработки экспериментальных данных, чаще всего представленных в виде массива, состоящего из пар чисел х и у. Необходимо заменить дискретную зависимость непрерывной функцией у = f(x), к которой предъявляются различные требования:
- она должна проходить через все экспериментальные точки – интерполяция данных и предсказывать результат за пределами изменения аргумента х – экстраполяция данных;
- задана в аналитическом виде и наилучшим образом приближается к экспериментальным точкам, не обязательно проходя через них – задача регрессии;
- она должна уменьшать погрешность измерений, присутствующую в экспериментальных данных (шумовая составляющая измерений) – задача фильтрации.
Рассмотрим решение первых двух задач.
Интерполяция
Интерполяция означает построение функции, аппроксимирующей зависимость у = f(x) в промежутках между точками хi . Самый простой вид интерполяции – линейный, в Mathcad предусмотрена функция linterp(x,y,t), где t – значение аргумента, при котором вычисляется интерполирующая функция (рис.1):
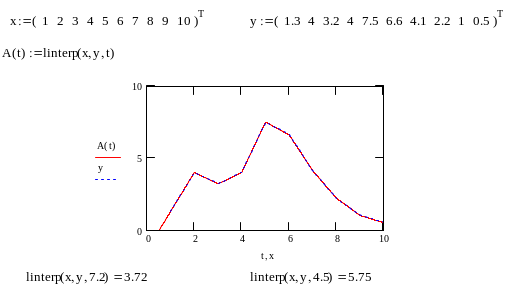
Рис. 1
Если желательно соединять экспериментальные точки гладкой кривой, то лучше всего реализовать интерполяцию с помощью кубических сплайнов и встроенной функции interp(s,x,y,t), где s – вектор вторых производных, созданных одной из сопутствующих функций.
В промежутках между экспериментальными точками аппроксимация осуществляется отрезками кубических парабол (кубическими сплайнами)
где аi – константы, подлежащие определению. Для этого предусмотрены сопутствующие функции:
- lspline(x,y) – вектор значений коэффициентов линейного сплайна;
- pspline(x,y) – вектор значений коэффициентов квадратичного сплайна;
- cspline(x,y) – вектор значений коэффициентов кубического сплайна.
Пример сплайн-интерполяции приведён ниже (рис. 2).
Рис. 2
Очевидно, что выбор вспомогательной функции существенно меняет результат экстраполяции данных за его пределами.
В Mathcad предусмотрен также более сложный тип интерполяции с помощью В-сплйнов, многомерная интерполяция и экстраполяция функцией предсказывания.
Регрессия
Выборка экспериментальных данных заменятся некоторой функцией f(x), минимизирующей совокупность ошибок. При этом задача сводится к выбору функции и определению её коэффициентов. Коэффициенты вычисляются из условия минимума тем или иным образом задаваемой функции ошибки. В качестве аппроксимирующих функций применяют кусочно-линейные функции, степенные, экспоненциальные и тригонометрические полиномы, гиперболические синусы и тангенсы и т.д.
Самый простой вид регрессии – линейный:
реализуется с помощью функции line(x,y) – результат – вектор из двух элементов – а и b или с помощью функций intercept(x,y) – коэффициент а линейной регрессии, slope(x,y)– коэффициент b– линейной регрессии (рис. 3).
В Mathcad имеется альтернативный алгоритм, реализующий медиан-медианную линейную регрессию для расчёта коэффициентов а и b: medfit(x,y) – рис. 3:
Рис. 3
Полиноминальная регрессия полиномом k степени осуществляется комбинацией встроенной функции s = regress(x,y,k), которая рассчитывает вектор коэффициентов для построения полиноминальной регрессии данных и полиноминальной интерполяции interp(s,x,y,t). Однако использование этой функции для аппроксимации кривой намагничивания дало отрицательный результат (рис. 4). Наилучший результат дала функция регрессии отрезками полиномов s = loess(x,y,span) + interp(s,x,y,t). Здесь span –некоторое число, которое задаёт степень сглаженности данных, в нашем случае 0.9). Результаты расчётов приведены на рис. 4
Рис. 4
Удовлетворительный результат получен с последним алгоритмом.
Если зависимость, описывающая массив данных, известна, можно использовать одну из следующих функций [ 3 ]:
- expfit(x,y,g)
– регрессия экспонентой
;
- lgsfit(x,y,g)
– регрессия логистической функцией
;
- sinfit(x,y,g)
– регрессия синусоидой
;
- pwfit(x,y,g)
– регрессия степенной функцией
;
- logfit(x,y,g)
– регрессия логарифмической функцией
;
- lnfit(x,y) – регрессия двухпараметрической логарифмической функцией
.
Однако применение этих функций требует точного знания вектора начальных условий g, состоящего из трёх элементов и задающего начальные значения a, b, c. Если функция хорошо приближает зависимость y =f(x), то начальные значения выбраны удачно.
С помощью функций linfit(x,y,F) можно осуществить регрессию в виде линейной комбинации функций F(x), задаваемых пользователем, либо с помощью функции genfit(x,y,g,G), где G(x,C) – векторная функция пользователя и её частных производных по каждому из параметров С. Последняя функция наиболее универсальная, но наименее точная и более трудная в использовании.
В качестве функций пользователя выбраны:
-
Наилучший результат получен для функций f1 и f3(рис. 5).
Порядок выполнения работы
Для таблично заданных функций аргумента х с помощью встроенных алгоритмов выполнить интерполяцию и определить вид зависимости y = f(x).
х |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
у1 |
0 |
4.1 |
15.7 |
36 |
68 |
95 |
150 |
у2 |
101 |
85 |
60 |
34 |
20 |
16 |
14 |
Сравнить полученные результаты графически и выбрать наилучшую зависимость.
Вопросы для самопроверки
На какие группы в зависимости от специфики решаемых задач можно разделить встроенные функции обработки данных?
Что такое интерполяция и экстраполяция?
В чём отличие интерполяции В-сплайнами от интерполяции кубическими сплайнами?
Что является задачей регрессионного анализа? Какие встроенные функции аппроксимации имеются в Mathcad?
Рис. 5
Литература
Макаров Е.Г. Инженерные расчёты в Mathcad. Учебный курс. – Спб.: Питер, 2003. – 448с.: ил.
Гурский Д.А. Вычисления в MathCAD / Д.А. Гурский. – Мн.: Новое знание, 2003. – 814с.: ил.
Кирьянов Д.В. Самоучитель Mathcad 12. – СПб.: БХВ-Петербург, 2004. – 576с.: ил.
Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. – СПб.: БХВ-Петербург, 2005. – 464с.: ил.
Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9 / Алексеев Е.Р., Чеснокова О.В. – M.: НТ Пресс, 2006. – 496с.: ил. – (Самоучитель).