Лабораторная работа № 9 Решение обыкновенных дифференциальных уравнений в Mathcad

Цель работы: закрепить знания о применении дифференциальных уравнений для анализа временных характеристик электрических цепей и систем управления; развить навыки и умения решать дифференциальные уравнения.

Введение

Дифференциальные уравнения – это уравнения, в которых неизвестными являются функции. Обыкновенное дифференциальное уравнение имеет единственное решение, если заданы начальные или граничные условия. Решить дифференциальное уравнение – значит определить неизвестную функцию на определённом интервале изменения её аргумента (в нашем случае это время t). Для численного интегрирования одного обыкновенного дифференциального уравнения n порядка можно использовать блок Given / Odesolve или встроенные функции.

Применение блока Given / Odesolve для решения уравнений первого порядка реализуется в три этапа:

- Given

- ввод дифференциального уравнения, разрешённого относительно первой производной, и начального условия с помощью логических операторов;

- Odesolve(t,t1), где t1 - конечное время;

- построение графика функции.

Имеется возможность выбирать метод решения – метод Рунге-Кутты с фиксированным шагом (по умолчанию) и адаптивный. Для этого нажатием правой мыши на области функции Odesolve вызывается контекстное меню и выбирается один из пунктов: Fixed или Adaptive.

Рассмотрим решение дифференциального уравнения первого порядка

Данное уравнение имеет точное аналитическое решение

и численное решение, полученное с помощью блока Given / Odesolve, легко можно проверить. Непосредственное применение этого блока дает неудовлетворительный результат (метод Рунге – Кутты с фиксированным шагом, рис. 1; адаптивный, кривая i1, рис. 2).

Для точного решения целесообразно применять функцию Odesolve(t,t1,m), где m – число шагов интегрирования на интервале решения. Пример применения этой функции приведён на рис. 2 (кривая i2). Здесь же показано точное аналитическое решение (кривая ir). Очевидно, что получен хороший результат.

Аналогично можно решать дифференциальные уравнения порядка выше первого. Начальные условия задаются на функцию и её производные до n-1 порядка включительно.

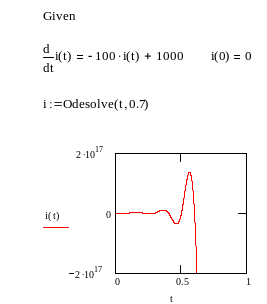
Рис. 1

Рис. 2

Для решения дифференциальных уравнений первого порядка и систем дифференциальных уравнений первого порядка в Mathcad предусмотрены три встроенные функции, обращение к которым выполняется одинаково:

- rkfixed(y0,t0,tk,m,D) – метод Рунге-Кутты четвёртого порядка с фиксированным шагом;

-Rkadapt(…) – метод Рунге-Кутты четвёртого порядка с переменным шагом;

-Bulstoer(…) - метод Булирша-Штера, целесообразно применять, если известно, что решение является гладкой функцией. Здесь у0 – вектор начальных условий в точке t0 размерностью n×1; t0 – начальное время; tk – конечное время; m – число шагов на интервале решения; D – векторная функция двух переменных, у и t. Результат расчёта выдается в виде матрицы размерностью m×2: первый столбец – аргумент, второй – значение функции . Эту особенность необходимо учитывать при построении графиков, ибо в качестве переменных рассматриваются величины u1¹ (функция) и u1⁰ (аргумент). Верхний индекс должен указываться с помощью панели Matrix →M^{< >}, т.е. u1^<1> и u1^<0>.

Пример расчёта приведён на рис. 3.

Рис. 3

Решение обыкновенных дифференциальных уравнений целесообразно выполнять с помощью преобразования Лапласа:

где f(t) – оригинал, F(p) – изображение, р = α +jω. Система интегро-дифференциальных уравнений относительно оригинала заменяется системой алгебраических уравнений относительно их изображений. После решения этой системы находятся изображения искомых функций в виде рациональной дроби:

a_k,b_j = const.

Для решения обратной задачи - перехода от изображения к оригиналу – можно воспользоваться таблицами соответствия оригинала изображению, разложением на простые дроби или теоремой разложения. На основании последней, если изображение Х(р) есть рациональная дробь и n ≥ m, то оригинал

где р_k – корни характеристического уравнения F₂(p) = 0; F^’₂ – производная от полинома знаменателя. Если F₂(p) = pF₃(p), то

.

На рис. 4 представлен листинг решения дифференциального уравнения четвёртого порядка при входном воздействии gg = 1.

Порядок выполнения работы

1. Решить с помощью блока Given - Odesolve(t,t1,m) дифференциальное уравнение при нулевых начальных условиях и двух значениях фазы включения Ψ:

Построить графики решений этих уравнений.

2. Решить с помощью встроенных функций следующие дифференциальные уравнения

Построить графики решений этих уравнений.

2. Решить дифференциальное уравнение

с помощью преобразования Лапласа и построить график функции при gg = 1.

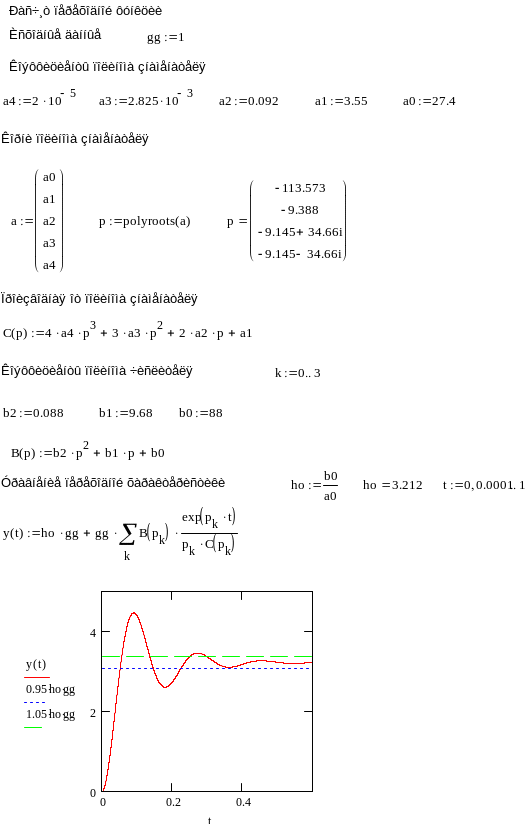
Рис. 4

Вопросы для самопроверки

1. Что значит решить дифференциальное уравнение?

2. Перечислите численные методы решений ОДУ и дайте их краткую характеристику.

3. В чём заключается преимущество операторного метода решения дифференциальных уравнений перед другими методами решений?

4. Какие блоки и встроенные функции Mathcad предназначены для решений ОДУ?

5. Почему для решения дифференциального уравнения необходимо задавать начальные условия?

Литература

Макаров Е.Г. Инженерные расчёты в Mathcad. Учебный курс. – Спб.: Питер, 2003. – 448с.: ил.

Гурский Д.А. Вычисления в MathCAD / Д.А. Гурский. – Мн.: Новое знание, 2003. – 814с.: ил.

Кирьянов Д.В. Самоучитель Mathcad 12. – СПб.: БХВ-Петербург, 2004. – 576с.: ил.

Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. – СПб.: БХВ-Петербург, 2005. – 464с.: ил.

Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9 / Алексеев Е.Р., Чеснокова О.В. – M.: НТ Пресс, 2006. – 496с.: ил. – (Самоучитель).