2. Метод ітерації.

Нехай дана система нелінійних рівнянь спеціального виду:

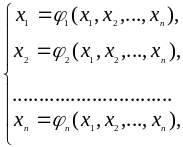(1)

де функції , ,... ., дійсно визначенні та непереривні на деякій області ізольованого рішення цієї системи.

Розглядаючи вектори і (x) = ( ₁ (x), ₂ (x), …. ., _n (x)), систему (1) можна записати у виді:

x = (x) (2)

Наприклад, для рішення системи двох нелінійних рівнянь з двома невідомими

потрібно перейти до рівностей:

Нехай вибрано початкове приближення ( , ), тоді

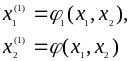
і k+1 приближення буде розраховуватися за формулами

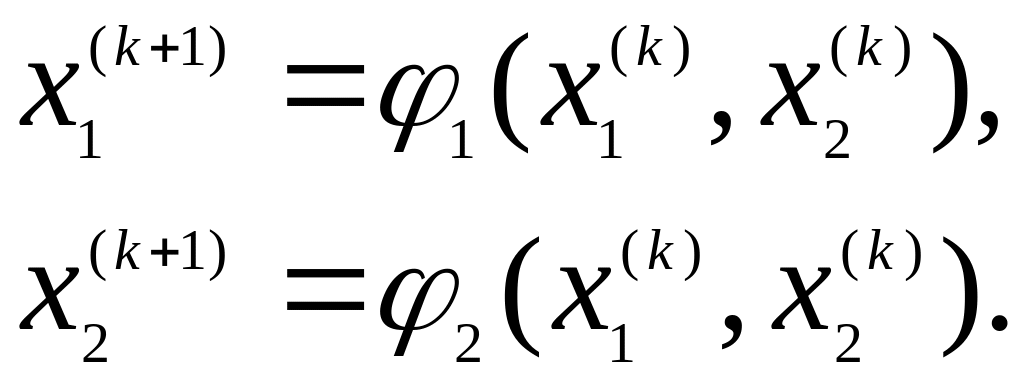
Відомо, що процес ітерації зводиться до рішення системи, якщо усі числа матриці

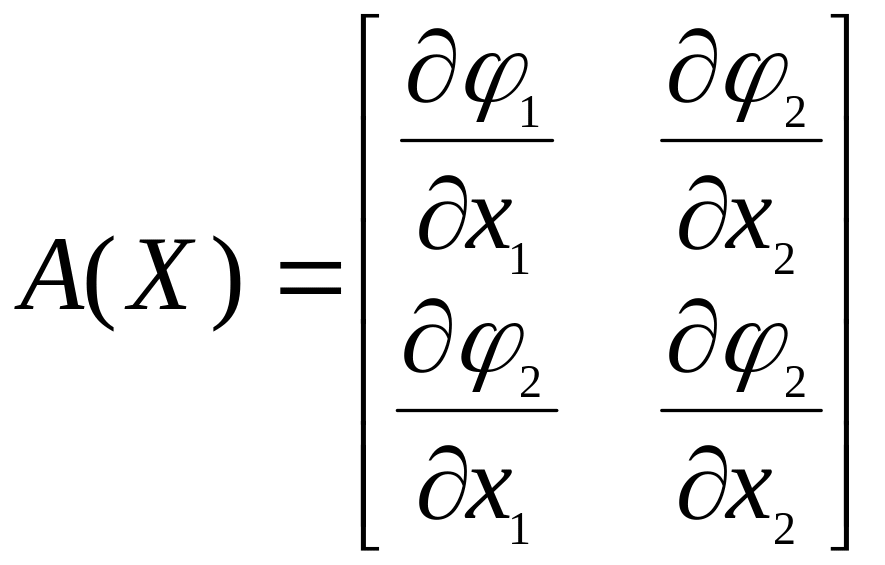
по модулю менше одиниці. Більш простою вимогою, використовуваною на практиці, є наступне: сума модулів частних похідних по кожному стовбці матриці повинна бути менша одиниці

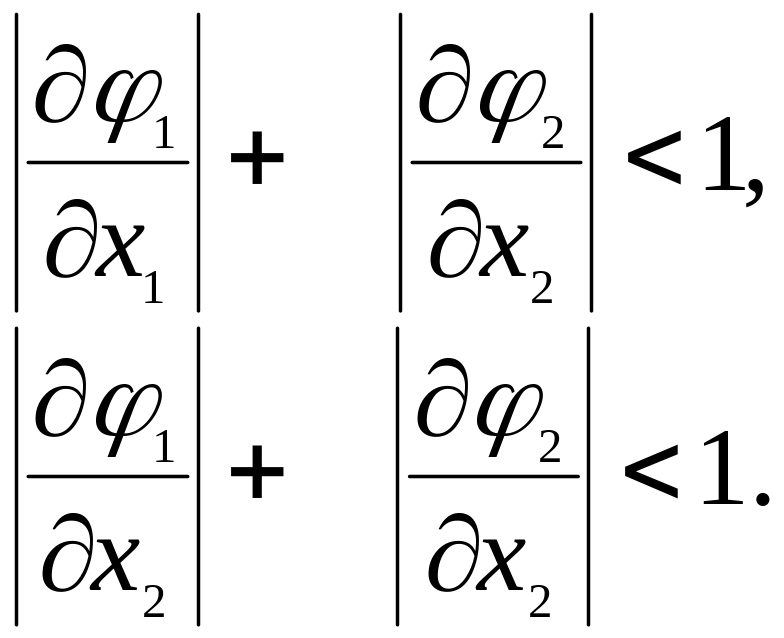
У випадку використання методу ітерацій до системи n рівнянь, k+1 ітерація буде будуватися по формулам

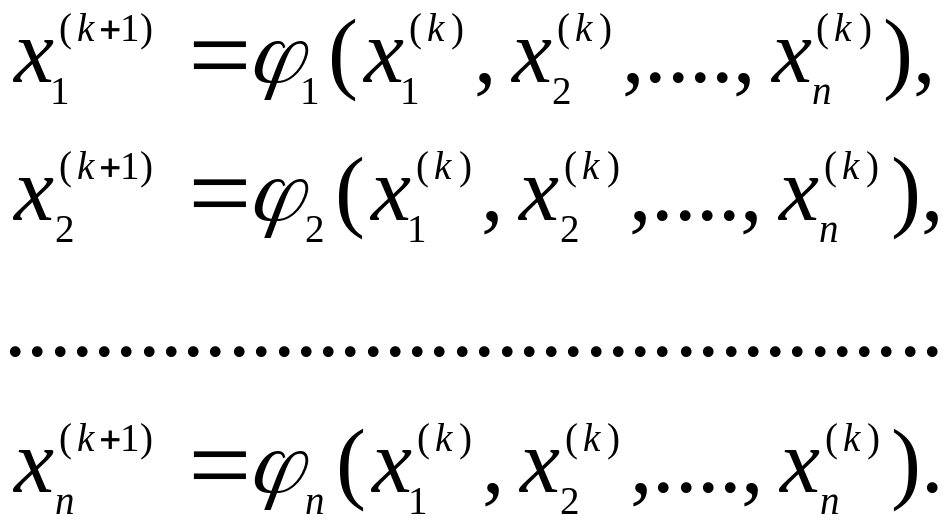
Тоді вимога сходження матиме вигляд:

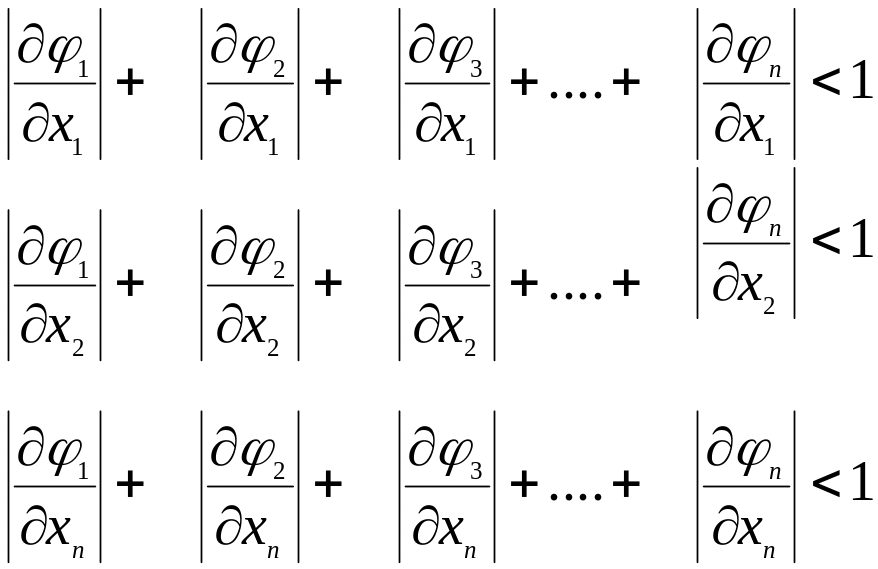
Слід відмітити, що ця вимога виповняється для дуже малого числа функцій, і тому метод ітерації дуже рідко використовується на практиці, не дивлячись на його простоту.

3. Метод градієнта (найшвидшого спуску)

Нехай маємо систему рівнянь:

або в матричному вигляді:

де

Допустимо, що функція дійсно непереривна та непреривно диференційована в загальній області визначення. Розглянемо функцію

Тоді рішення даної системи зводиться до мінімізації цієї функції.

Для мінімізації по методу спуску вибирається початковий вектор Х⁰, а потім шукається напрямлення спуска до рішення , таке щоб

для векторів Х ⁽¹⁾ виду . Тут - скалярна величина, постійна для даної ітерації і знаходить величину шагу за напрямом .

Методи спуску розрізняються в залежності від вибору напрямлення спуска. Одним із найкращих направлень є напрямлення градієнта

Функція Ф (Х ^(і)) задається в n-мірному просторі сімейства гіперповерхонь і градієнт вирішує напрям найшвидшого спуска. Тому саме воно використовується у методі найшвидшого спуска для мінімізації функції.

Другою проблемою в методах найшвидшого спуску є вибір величини шагу , на який потрібно про двинутися вздовж напряму зменшення функції.

Спробуємо вибрати оптимальний шаг для - ітерації методу найшвидшого спуска і побудувати вектор

для якого функція приймає менше значення, чим .

Розкладемо функцію

в ряд Тейлора та обмежившись членами другого порядку меншості отримаємо

(3)

Тоді значення , для якого функція прийме мінімальне значення, визначається із умови Про диференціювавши рівняння (3) по і враховуючи, що

отримаємо:

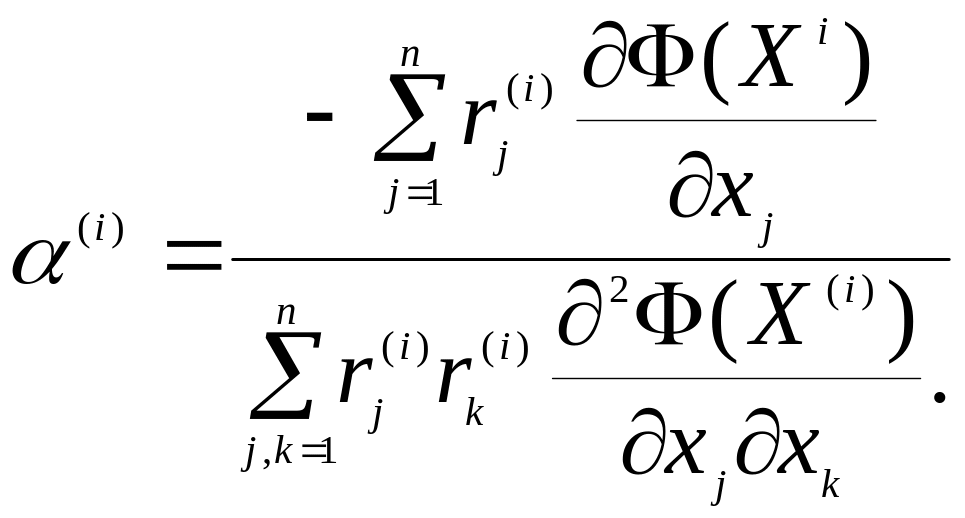(4)

Оскільки в методі найшвидшого спуску компоненти градієнта мають вигляд

то формула (4) після підстановки цих рівнянь перейде до вигляду

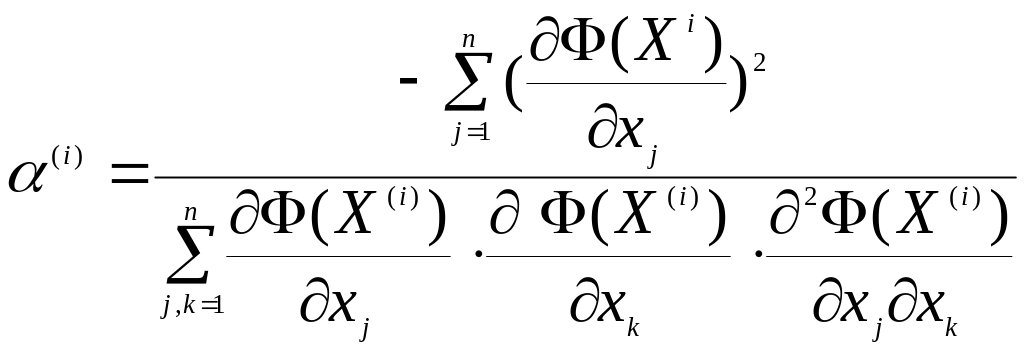(5)

Формула (5) дуже складна оскільки потребує рахування других часних похідних.

На практиці завжди використовується наступний варіант знаходження .

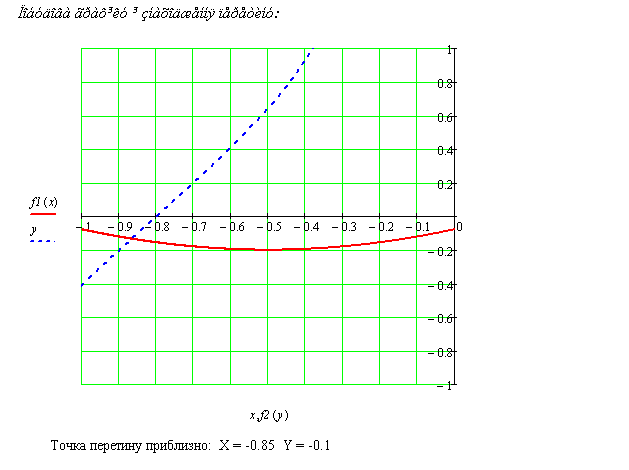
Нехай значення Ф (Х) змінюється вздовж напрямку градієнта . Розглянемо точку пересікання кривої та касатільної в точці з осю .

Вона буде розраховуватися наступним чином:

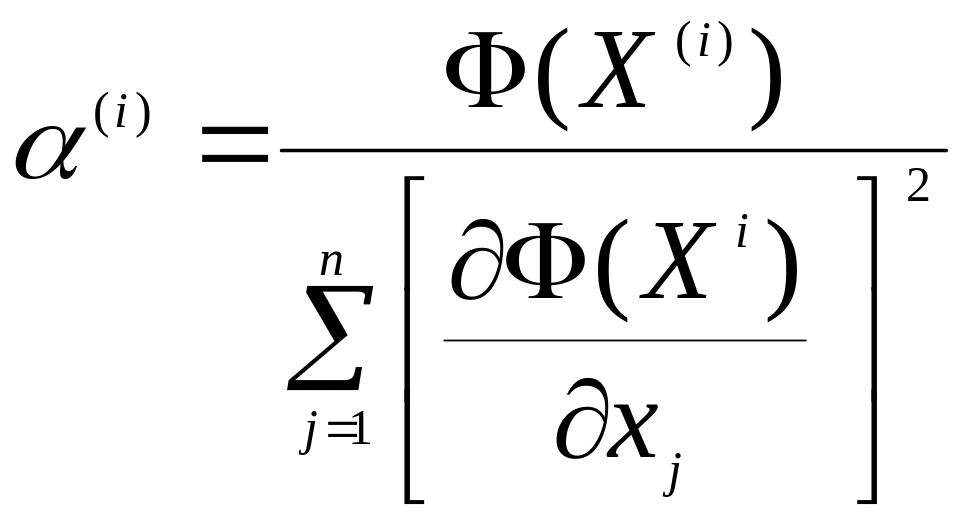. (6)

Як бачимо, в цьому випадку рахується просто, але сходження метода може бути дуже повільно. Тому інколи на практиці використовують наступну модифікацію.

Для кожної ітерації метода рахують значення функціонала при , а потім при і будують квадратичне наближення функціонала, який проходить через три точки

. Продиференціювавши отримане рівняння по та прирівнявши похідну, получимо наступне рівняння для

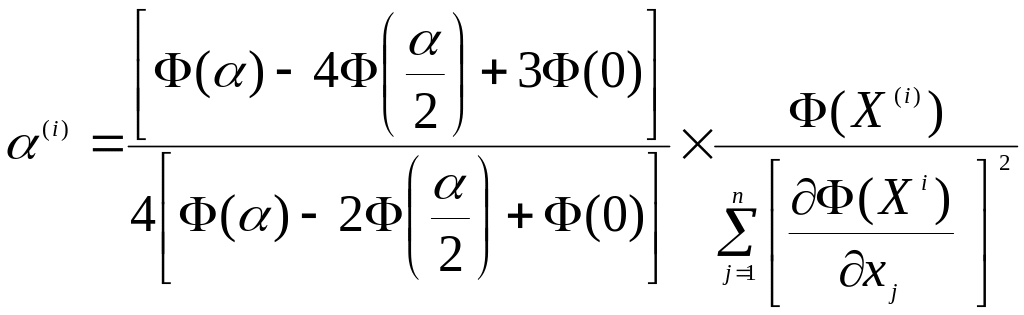(7)

Практика показує, що хоча цей варіант більш громіздкий, так як у порівнянні з формулою (5) доводиться додатково рахувати два значення функції , але метод сходиться набагато швидше.

Інколи характер Ф (Х) такий, що аналітичне рівняння для частних похідних має надто складний вигляд і рахувати їх надто складно.

Також слід відмітити, що якщо в області шуканого рішення є локальні мінімуми, то метод спуска може не привести до шукаємого рішення, а можуть зійтися до одного з цих мінімумів. Практично часто спуск буває дуже повільним навіть при відсутності локальних мінімумів.

Порядок рахування в методі найшвидшого спуска наступний:

• знаходиться аналітичне рівняння для градієнта ;

• вибирають початкове приближення вектора невідомих ;

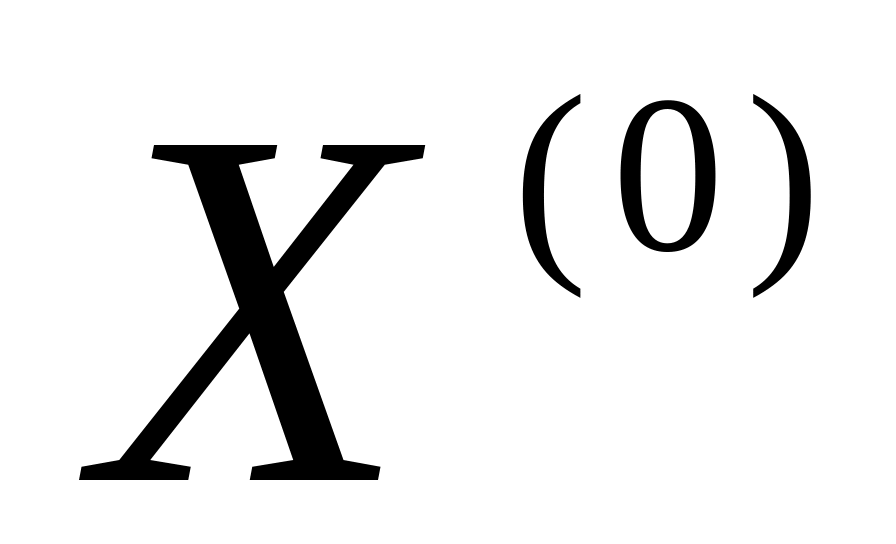• вираховують координати градієнта 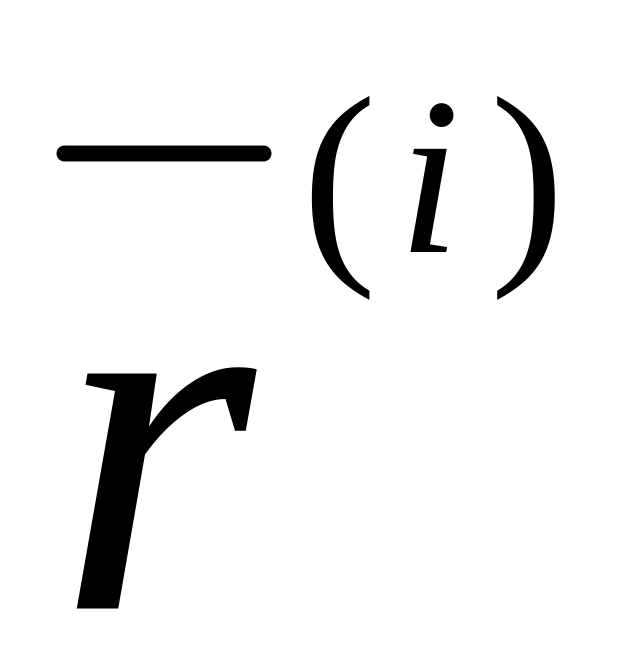в точці ;

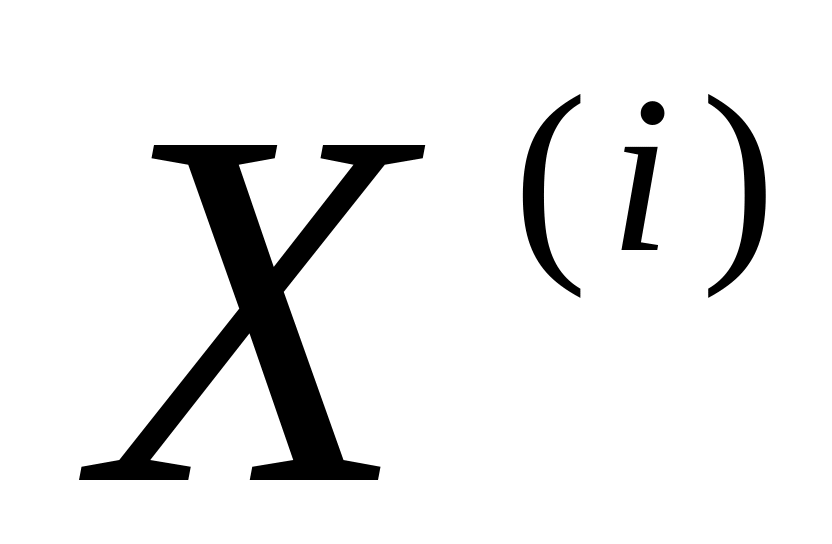• вираховують шаг по градієнту по формулам (6) або (7);

• вираховують уточнений вектор невідомих .

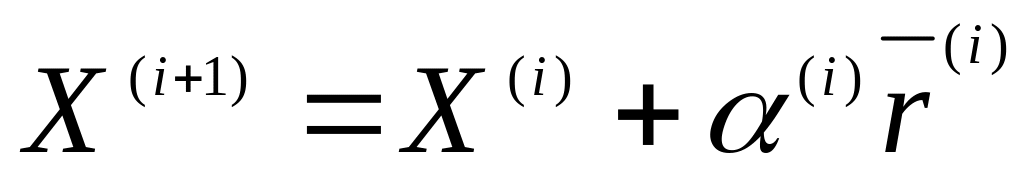РОЗДІЛ 5

РІШЕННЯ СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ.

Певна кількість лінійних рівнянь щодо тих самих невідомих утворюють систему лінійних рівнянь.

Рішенням системи лінійного рівняння називають набір чисел c₁, c₂, ..., c_n, що звертає всі рівняння в тотожності після підстановки їх замість відповідних невідомих.

Система лінійних рівнянь може мати як одне єдине рішення, так і нескінченну безліч рішень (невизначену система); може також виявитися, що система лінійних рівнянь не має жодного рішення (неспільна система).

  Найчастіше зустрічається випадок, коли число рівнянь збігається з числом невідомих. Одне лінійне рівяння з один невідомим має вид:

  ax = b;

  рішенням його при а  0 буде число b/a. Система двох лінійних рівнянь із двома невідомими має вигляд:

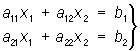   (1)

  де a₁₁, a₁₂, a₂₁, a₂₂, b₁, b₂— які-небудь числа. Рішення системи (1) можна одержати за допомогою визначників:

  ,

  ;

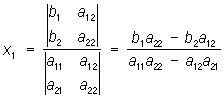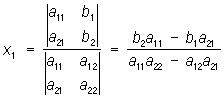  тут передбачається, що визначник, що 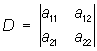 стоїть в знаменнику, відмінний від нуля. У чисельниках стоять визначники, які виходять з D заміною в ньому одного стовпця стовпцем вільних членів b₁, b₂; у вираженні для першого невідомого x₁ заміняється перший стовпець, а у вираженні для другого невідомого x₂ — другий.

  Аналогічне правило застосовне і при рішенні будь-якої системи і лінійного рівняння з n невідомими, тобто системи виду:

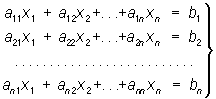   (2)

  тут a_ij і b_i (i, j = 1, 2, ..., n) — довільні числові коефіцієнти; числа b₁, b₂, ..., b_n називають звичайно вільними членами. Якщо визначник D = a_ij системи (2), складений з коефіцієнтів a_ij при невідомих, відмінний від нуля, то рішення виходить у такий спосіб: k-e (k = 1, 2, ..., n) невідоме x_k дорівнює дробу, у знаменнику якої коштує визначник D, а в чисельнику — визначник, отриманий з D заміною в ньому стовпця з коефіцієнтів при відшукуванні невідомого (к-го стовпця) стовпця вільних членів b₁, b₂, ..., b_n. Якщо D = 0, то система (2) або не має жодного рішення, або має нескінченна безліч рішень.

  Якщо всі b_i = 0 (систему лінійних рівнянь називають у цьому випадку однорідною), то при D  0 рішення системи (2) буде нульовим (тобто всі x_k = 0). У практиці часто, однак, зустрічаються однорідні системи лінійних рівнянь з числом рівнянь на 1 менше числа невідомих, тобто системи виду:

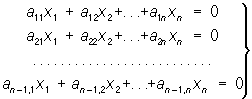   (3)

  Рішення такої системи неоднозначне; з неї, як правило, можна знайти тільки відношення невідомих:

  x₁ : x₂ : ... : x_n = D₁ : D₂ : ... : D_n,

  де D_n — помножений на (—1)^k визначник, отриманий з матриці коефіцієнтів a_ij системи (3) викреслюванням якогось стовпця (це правило застосовне тільки тоді, коли хоча б один з визначників D_i відмінний від 0).

  Уперше рішення систем (2) було отримано Г. Кратером у 1750; правило для перебування рішення цих систем носить дотепер назву правила Крамера. Побудова повної теорії систем лінійних рівнянь було закінчено тільки через 100 років Л.Кронекером.

  Загальна система m лінійних рівнянь з n невідомими має вид:

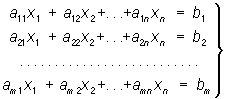   (4)

  Питання про спільність системи лінійних рівнянь (4), тобто питання про існування рішення, зважується порівнянням рангів матриць

 

  і

 

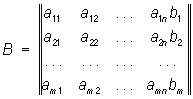
  Якщо ранги збігаються, то система сумісна; якщо ранг матриці В більше рангу матриці Л, то система несумісна (теорема Кронекера — Капеллі).

У випадку спільності системи, її рішення можна знайти в такий спосіб. Знайшовши в матриці А відмінний від нуля мінор найбільшого порядку м, відкидають m — r рівнянь, коефіцієнти яких не ввійшли в цей мінор ( рівняння, що відкидаються, будуть наслідками які залишилися, і тому їх можна не розглядати); у рівняннях, які залишилися, переносять праворуч той невідомі, коефіцієнти яких не ввійшли в обраний мінор (вільні невідомі).

Додавши вільним невідомим будь-які числові значення, одержують систему з r рівнянь з r невідомими, яку можна вирішити за правилом Крамера. Знайдені значення r невідомих разом зі значеннями вільних невідомих дадуть деяку частку (тобто одне з багатьох можливих) рішення системи (4). Можна, не даючи вільним невідомим конкретних значень, безпосередньо виразити через них інші невідомі. Так виходить загальне рішення, тобто рішення, у якому невідомі виражені через параметри; даючи цим параметрам довільні значення, можна одержати всі приватні рішення системи.

 

Однорідні системи лінійних рівнянь можна вирішувати таким ж способом. Рішення їх володіють тими властивістями, що сума, різниця і взагалі будь-яка лінійна комбінація рішень (розглянутих як n-мірні вектори) також буде рішенням системи. Іншими словами: сукупність усіх рішень однорідної системи Л. у. утворить лінійний підпростір n-мірного векторного простору. Систему рішень, що самі лінійно незалежні і дозволяють виразити будь-яку іншу рішення у виді їх лінійної комбінації (тобто базис лінійного підпростору), називають фундаментальною системою рішень однорідної системи лінійних рівнянь.

  Між рішеннями системи лінійних рівнянь (4) і відповідної однорідної системи лінійних рівнянь (тобто рівнянь з тими ж коефіцієнтами при невідомих, але з вільними членами, рівними нулю) існує простий зв'язок: загальне рішення неоднорідної системи виходить із загального рішення однорідної системи додатком до нього якого-небудь приватного рішення неоднорідної системи лінійних рівнянь.

  Великої наочності викладу в теорії лінійних рівнянь можна домогтися, використовуючи геометричну мову. Залучаючи при цьому до розгляду лінійні оператори у векторних просторах (розглядаючи рівняння виду Ax = b, А — лінійний оператор, х и b — вектори), легко встановити зв'язок розглянутих алгебраїчних лінійних рівнянь з лінійних рівнянь у безкінечно мірних просторах (системи лінійних рівнянь з нескінченним числом невідомих), зокрема з лінійних рівнянь у функціональних просторах, наприклад лінійні диференціальні рівняння, лінійні інтегральні рівняння. 

Застосування правила Крамера при практичному рішенні великого числа лінійних рівнянь може зустріти значних труднощів, тому що перебування визначників високого порядку зв'язано з занадто великими обчисленнями. Були тому розроблені різні методи чисельного (наближеного) рішення систем лінійних рівнянь.

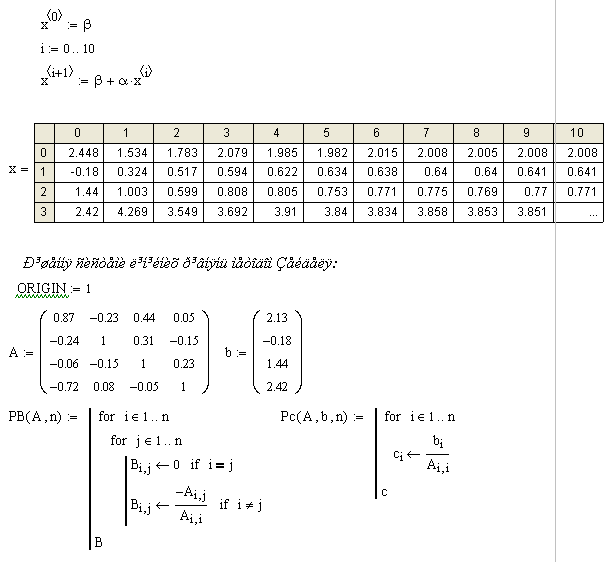
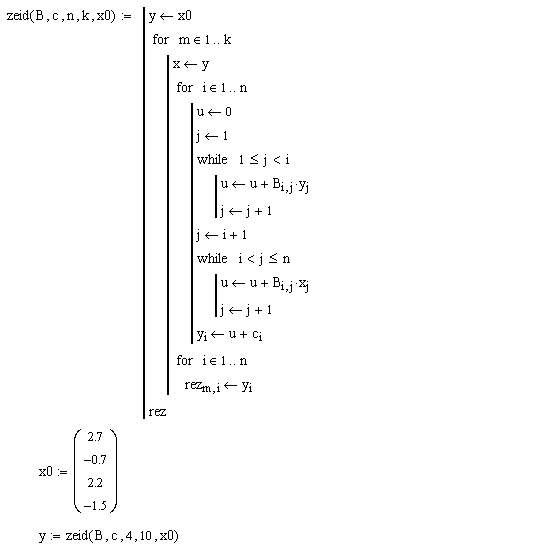
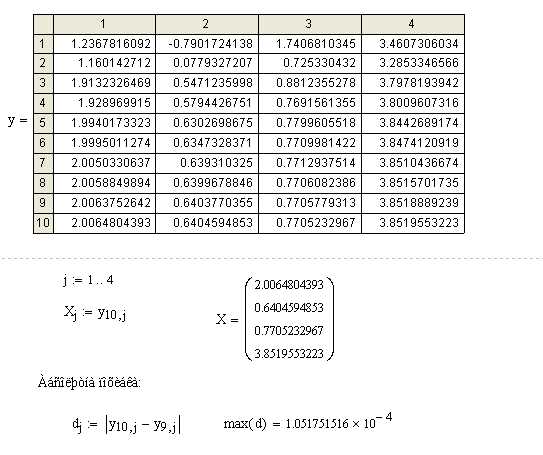
РОЗДІЛ 6

РІШЕННЯ ДИФЕРЕНЦІЙНИХ РІВНЯНЬ.